河南省郑州市二七区二七区京广实验中学2023-2024学年八年级上学期第二次月考数学试题

这是一份河南省郑州市二七区二七区京广实验中学2023-2024学年八年级上学期第二次月考数学试题，共11页。试卷主要包含了在实数中，最小的数是，下列各命题是真命题的是等内容，欢迎下载使用。

一．选择题（每小题3分，共30分）
1．在实数中，最小的数是（ ）
A．0B．C．D．
2．为庆祝2023年5月30日神舟十六号成功发射，学校开展航天知识竞赛活动经过几轮筛选，某班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛，经统计，四名同学成绩的平均数（单位：分）及方差（单位：分）如表，根据表中数据，要选一名成绩好且状态稳定的同学参赛，应选择（ ）
A．甲B．乙C．丙D．丁
3．在平面直角坐标系的第二象限内有一点，它到轴的距离为3，到轴的距离为5，则点的坐标为（ ）
A．B．C．D．
4．用加减法解方程组时，下列四种变形中正确的是（ ）
A．B．C．D．
5．下列各命题是真命题的是（ ）
A．如果，那么B．是一组勾股数
C．两条直线被第三条直线所截，同位角相等D．三角形的任意两边之和大于第三边
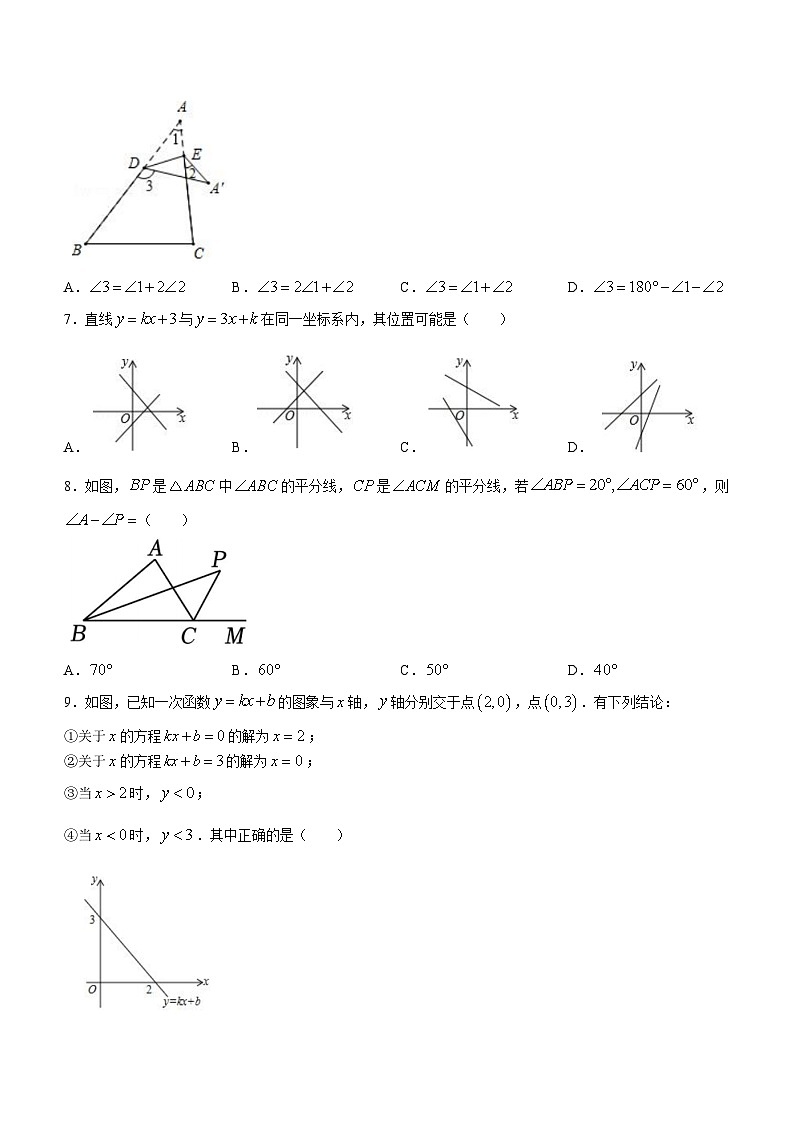
6．如图，将沿折叠，折痕为，则图中之间的关系中，下列式子中正确的是（ ）
A．B．C．D．
7．直线与在同一坐标系内，其位置可能是（ ）
A．B．C．D．
8．如图，是中的平分线，是的平分线，若，则（ ）
A．B．C．D．
9．如图，已知一次函数的图象与轴，轴分别交于点，点．有下列结论：
①关于的方程的解为；
②关于的方程的解为；
③当时，；
④当时，．其中正确的是（ ）
A．①②③B．①③④C．②③④D．①②④
10．如图，直线与轴、轴分别交于点和点，点、分别为线段的中点，点为上一动点，当最小时，点的坐标为（ ）
A．B．C．D．
二．填空题（每小题3分，共15分）
11．已知为实数，则点一定在第______象限．
12．若二元一次方程组的解为，则一次函数与的图象的交点坐标为______．
13．点是直线上的两点，则______0（填“”或“”）．
14．如图，在轴上分别截取，使，再分别以点、为圆心，以大于的长度为半径画弧，两弧交于点．若的坐标为，则______．
15．两块含角的三角尺叠放如图所示，现固定三角尺不动，将三角尺绕顶点顺时针转动，使两块三角尺至少有一组边互相平行，且点在直线的上方，则所有可能符合的度数为______．
三．解答题（共7小题，共55分）
16．（每小题3分，共6分）计算：
（1）；（2）；
17．（分）蓬勃发展的快递业，为全国各地的新鲜水果及时走进千家万户提供了极大便利．不同的快递公司在配送、服务、收费和投递范围等方面各具优势．樱桃种植户小丽经过初步了解，打算从甲、乙两家快递公司中选择一家合作，为此，小丽收集了10家樱桃种植户对两家公司的相关评价，并整理、描述、分析如下：
．配送速度得分（满分10分）：
甲：6 6 7 7 7 8 9 9 9 10
乙：6 7 7 8 8 8 8 9 9 10
．服务质量得分统计图（满分10分）：
．配送速度和服务质量得分统计表：
根据以上信息，回答下列问题：
（1）表格中的______；______（填“”“”或“”）；
（2）综合上表中的统计量，你认为小丽应选择哪家公司？请说明理由；
（3）为了从甲、乙两家公司中选出更合适的公司，你认为还应收集什么信息？（列出一条即可）
18．（分）（1）如图1，已知，，．求出的度数．
（2）“三等分一个任意角”是数学史上一个著名问题，今天人们已经知道，仅用圆规直尺是不可能做出的．在探索中，有人曾利用过如图2所示的图形，其中，是长方形，，是延长线上一点，是上一点，并且，请证明
图1 图2
19．（分）森林火灾是一种常见的自然灾害，危害很大，随着中国科技、经济的不断发展，开始应用飞机洒水的方式扑灭火源．如图，有一台救火飞机沿东西方向，由点飞向点，已知点为其中一个着火点，且点与直线上两点的距离分别为和，又，飞机中心周围以内可以受到洒水影响．
（1）着火点受洒水影响吗？为什么？
（2）若飞机的速度为，要想扑灭着火点估计需要，请你通过计算判断着火点能否被扑灭？
20．（分）甲无人机从地面起飞，乙无人机从距离地面高的楼顶起飞，内甲、乙两架无人机所在的位置距离地面的高度（单位：）与无人机上升的时间（单位：）之间的关系如所示．
（1）分别求出甲、乙两架无人机所在的位置距离地面的高度与无人机上升的时间之间的关系式；
（2）当两架无人机的高度差为，求它们的上升时间．
21．（分）为了弘扬爱国主义精神，某中学组织八年级学生到郑州市二七纪念塔展览，现有两种车型可供选择．已知2辆型车和1辆型车可以载学生100名；1辆型车和2辆型车可以载学生110人，该学校八年级共有320名学生，根据题目提供的信息，解决下列问题：
（1）型车每辆可分别载学生多少人？
（2）若租一辆型车需要1000元，租一辆型车需要1200元，请你设计租车方案，使得恰好运送完学生并且租车费用最少．
22．（分）如图，一次函数的图象与轴交于点，与轴交于点，与正比例函数的图象交于点，且点的横坐标为2，点为轴上的一个动点．
备用图
（1）求点的坐标和的值；
（2）连接，当与的面积相等时，求点的坐标；
（3）连接，是否存在点使得为等腰三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．
参考答案
一．选择题（共10小题）
1-5 B A A C D6-10 B A D A C
二．填空题（共5小题）
11．四．12．．13．．14．4．
15．或和或．
三．解答题（共6小题）
16．（1） （2）
17．解：（1）甲公司配送速度得分从小到大排列为：6 6 7 7 7 8 9 9 9 10，
一共10个数据，其中第5个与第6个数据分别为，
所以中位数．
，
，，故答案为：7.5 ；
（2）小丽应选择甲公司（答案不唯一），理由如下：
配送速度得分甲和乙的得分相差不大，服务质量得分甲和乙的平均数相同，但是甲的方差明显小于乙的方差，
甲更稳定，小丽应选择甲公司；
（3）还应收集甲、乙两家公司的收费情况．（答案不唯一，言之有理即可）
18．解：（1）设为，
，，
，
，，即，
解得，
，，
（2）①在中，，
，
，
，
，
．
19．解：（1）着火点受洒水影响．
理由：如图，过点作于，
由题意知，
，
，是直角三角形，
，
，，
飞机中心周围以内可以受到洒水影响，着火点受洒水影响；
（2）当时，飞机正好喷到着火点，
在中，，
，
飞机的速度为（秒），
秒秒，着火点能被扑灭，
答：着火点能被扑灭．
20．解：（1）设甲无人机与之间的关系式为．将坐标代入，
得，解得．
甲无人机与之间的关系式为．
设乙无人机与之间的关系式为．将坐标和代入，
得，解得．
乙无人机与之间的关系式为．
（2）根据题意，得，即，解得或．
当两架无人机的高度差为，它们的上升时间为或．
21．解：（1）设每辆型车可载学生人，每辆型车可载学生人，
依题意，得：，解得：．
答：每辆型车可载学生30人，每辆型车可载学生40人．
（2）设租型车辆，租型车辆，
依题意，得：，解得：．
均为非负整数，．
当时，租车费用为（元）；
当时，租车费用为（元）；
当时，租车费用为（元）．
，
不租型车、8辆型车．
22．解：（1）将代入，得点的坐标为．
一次函数的图象与轴交于点，
，即．
将点代入，得，解得．
（2），中边上的高为2，
．
在中，令，得，
，即中，边上的高为2.5，
，解得．
又或．
（3）存在，理由：
如图1，过点作轴于点，则，
，，．
图1
①当时，．
因为此时点的坐标为或；
②当时，由等腰三角形的性质易得．
．
此时点的坐标为；
③当时，如图2，
图2
设，则，
，，
解得：，此时点的坐标为．
综上可知，存在点使得为等腰三角形，点的坐标为：或或或．甲
乙
丙
丁
平均数
97
95
97
93
方差
0.3
1.2
1.3
0.6
项目
统计量
快递公司
配送速度得分
服务质量得分
平均数
中位数
平均数
方差
甲
7.8
7
乙
8
8
7