数学七年级下册1 认识三角形课后作业题

这是一份数学七年级下册1 认识三角形课后作业题，共12页。试卷主要包含了1　三角形，如图,图中三角形的个数为，如图,下列说法错误的是等内容，欢迎下载使用。

9.1 三角形
9.1.1 认识三角形
基础过关全练
知识点1 三角形的有关概念
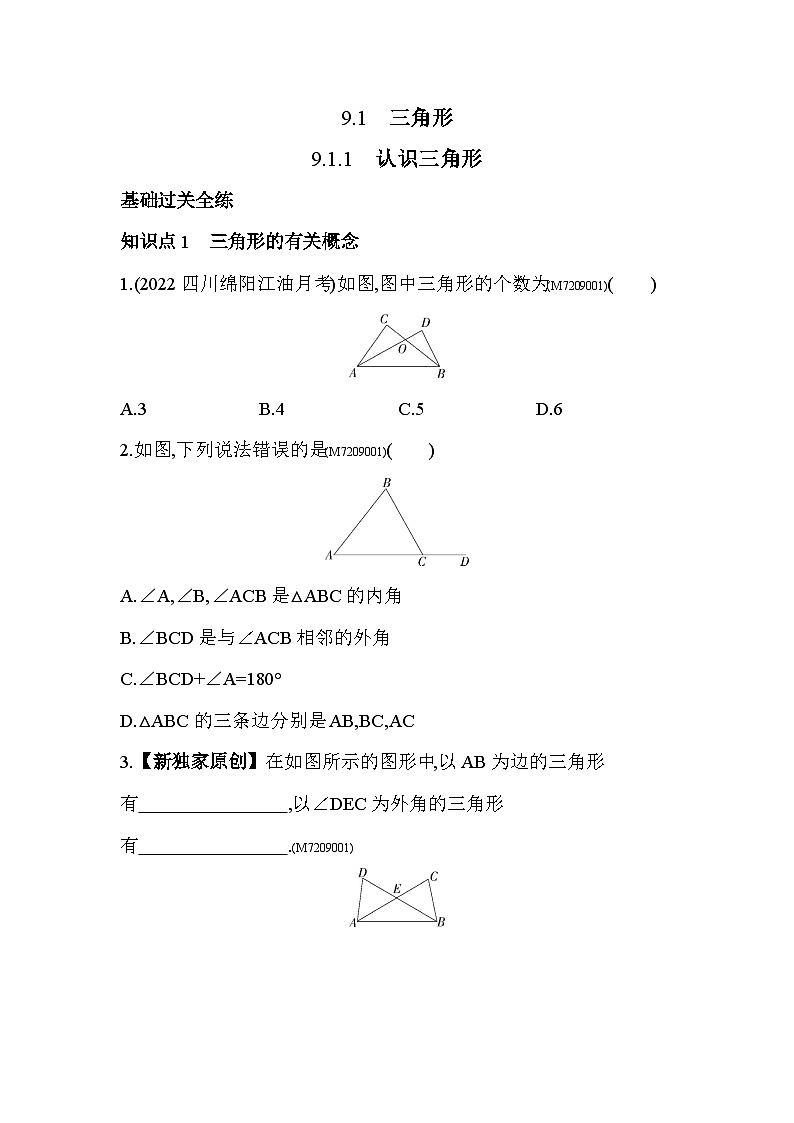
1.(2022四川绵阳江油月考)如图,图中三角形的个数为(M7209001)( )
A.3 B.4 C.5 D.6
2.如图,下列说法错误的是(M7209001)( )
A.∠A,∠B,∠ACB是△ABC的内角
B.∠BCD是与∠ACB相邻的外角
C.∠BCD+∠A=180°
D.△ABC的三条边分别是AB,BC,AC
3.【新独家原创】在如图所示的图形中,以AB为边的三角形有 ,以∠DEC为外角的三角形有 .(M7209001)
知识点2 三角形的分类
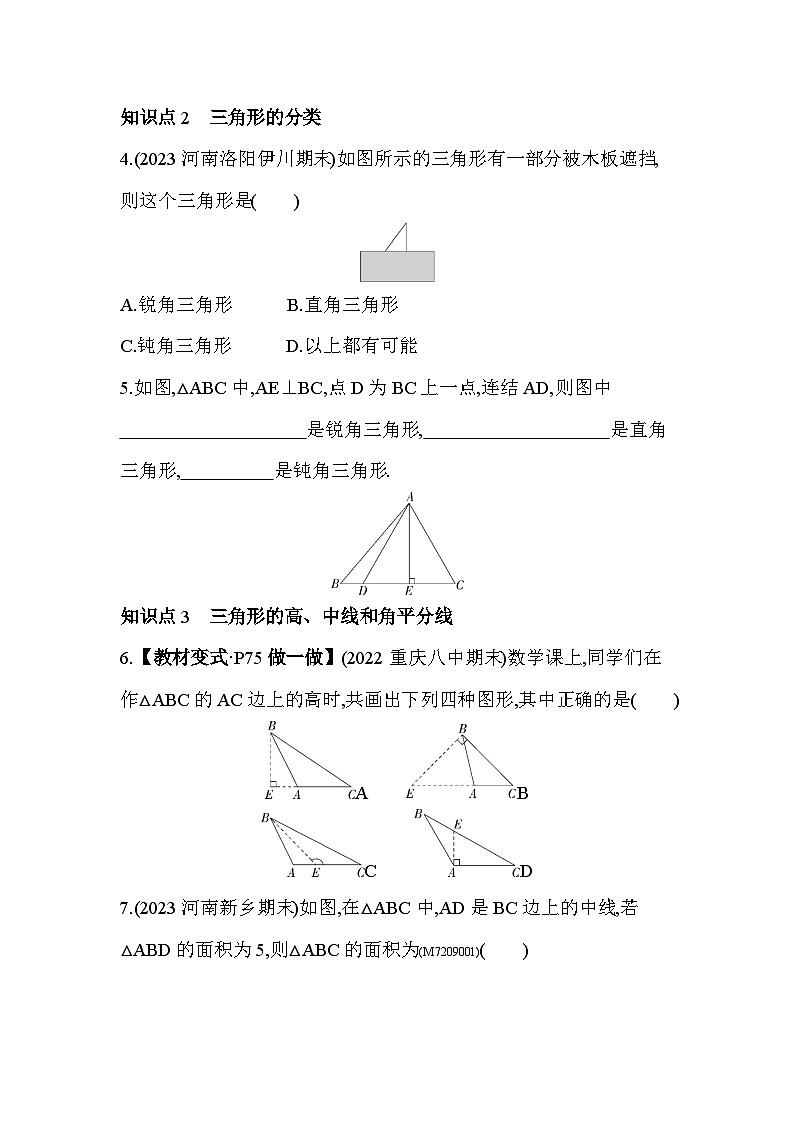
4.(2023河南洛阳伊川期末)如图所示的三角形有一部分被木板遮挡,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
5.如图,△ABC中,AE⊥BC,点D为BC上一点,连结AD,则图中
是锐角三角形, 是直角三角形, 是钝角三角形.
知识点3 三角形的高、中线和角平分线
6.【教材变式·P75做一做】(2022重庆八中期末)数学课上,同学们在作△ABC的AC边上的高时,共画出下列四种图形,其中正确的是( )
A B
C D
7.(2023河南新乡期末)如图,在△ABC中,AD是BC边上的中线,若△ABD的面积为5,则△ABC的面积为(M7209001)( )
A.14 B.12 C.10 D.8
8.(2023山东泰安泰山月考)如图,AD,AE,AF分别是△ABC的中线,角平分线,高,则下列结论中错误的是(M7209001)( )
A.BC=2CD B.∠BAE=12∠BAC
C.∠AFB=90° D.AE=CE
9.(2023河南洛阳伊川期末)如图,△ABC中AB边上的高是(M7209001)( )
A.AD B.BE C.CF D.BF
10.(2022河南郑州中学期中)如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=12∠ACB
D.CE是△ABC的角平分线
11.【等积法】【新独家原创】如图,在△ABC中,BA⊥AC,AD⊥BC,垂足分别为A、D,已知AB=6,AC=8,BC=10,则BC边上的高的长为( )
A.10 B.8 C.6 D.4.8
12.(2023福建泉州五中模拟)如图,AD是△ABC的中线,AB=8,AC=6.若△ACD的周长为16,则△ABD的周长为 .(M7209001)
能力提升全练
13.(2022浙江杭州中考,5,★☆☆)如图,CD⊥AB于点D,已知∠ABC是钝角,则(M7209001)( )
A.线段CD是△ABC的AC边上的高线
B.线段CD是△ABC的AB边上的高线
C.线段AD是△ABC的BC边上的高线
D.线段AD是△ABC的AC边上的高线
14.(2023河南郑州四中期中,8,★★☆)在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长长3,AB的长与AC的长的和为13,则AC的长为(M7209001)( )
A.5 B.6 C.7 D.8
15.【一题多变·运用三角形中线的性质求三角形面积】
【双中点模型】(2022江苏常州中考,14,★★☆)如图,在△ABC中,E是中线AD的中点.若△AEC的面积是1,则△ABD的面积是 .
[变式1·由两条中线变为三条中线](2023河南驻马店遂平期末,10,★★☆)如图,在△ABC中,D是BC中点,E是AD中点,连结BE、CE,若△ABC的面积为20,则△BCE的面积为( )
A.5 B.10 C.15 D.18
[变式2·由两条中线变为两条中线+三等分点](2022江苏扬州邗江实验学校期中,7,★★☆)如图,在△ABC中,D,E分别是BC,AD的中点,点F在BE上,且EF=2BF,若S△BCF=2 cm2,则S△ABC=( )
A.3 cm2 B.6 cm2 C.8 cm2 D.12 cm2
[变式3·由三角形面积变为四边形面积](2023山西临汾期末,9,★★☆)如图,D,E,F分别是BC,AD,AC的中点,若阴影部分的面积为9,则△ABC的面积为( )
A.24 B.20 C.18 D.16
16.(2023山东聊城东阿期末,25,★★☆)如图,在△ABC中,
∠C=90°,AC=8 cm,BC=6 cm,AB=10 cm,若动点P从点C开始,沿着C→A→B→C的路径运动,且速度为每秒2 cm,设运动的时间为t秒.(M7209001)
(1)当t为何值时,CP把△ABC分成周长相等的两部分?
(2)当t为何值时,CP把△ABC分成面积相等的两部分?
备用图
素养探究全练
17.【推理能力】(2022云南大理模拟)如图,AP1为△ABC的中线,AP2为△AP1C的中线,AP3为△AP2C的中线,……,按此规律,APn为△APn-1C的中线.若△ABC的面积为S,则△APnC的面积为(M7209001)( )
A.S2n-2 B.S2n-1 C.S2n D.S2n+1
18.【推理能力】观察如图所示的图形,回答下列问题.(M7209001)
(1)图②中有 个三角形;图③中有 个三角形;图④中有 个三角形;……,猜测图⑦中有 个三角形;
(2)结合(1)猜测图中有几个三角形(用含n的代数式表示).
答案全解全析
基础过关全练
1.C 题图中的三角形有△AOC、△BOD、△AOB、△ABC、△ABD,共5个.故选C.
2.C 三角形的一个外角与它相邻的内角互为补角.
3.△ABD,△ABC,△ABE;△ADE,△BCE
4.D 题图中只能看到三角形的一个角是锐角,其余两个角可以都是锐角或其中一个角是钝角或其中一个角是直角.故选D.
5.△ABC,△ADC;△ADE,△ACE,△ABE;△ABD
6.A A.BE是△ABC的AC边上的高,符合题意;B.BE不是△ABC的AC边上的高,不符合题意;C.BE不是△ABC的AC边上的高,不符合题意;D.AE是△EAC的AC边上的高,不是△ABC的AC边上的高,不符合题意.故选A.
7.C ∵AD是BC边上的中线,△ABD的面积为5,
∴△ABC的面积=2×5=10.故选C.
8.D ∵AD,AE,AF分别是△ABC的中线,角平分线,高,∴BC=2BD=2DC,∠BAE=∠CAE=12∠BAC,∠AFB=∠AFC=90°,故选项A、B、C正确,选项D错误,故选D.
9.C 因为点C到AB边所在直线的垂线段是CF,所以AB边上的高是CF,故选C.
10.D ∵∠1=∠2,∠3=∠4,∴BD是△ABC的角平分线,CE是△BCD的角平分线,故选项A、B正确;∠3=12∠ACB,选项C正确;CE是△ABC的角平分线是错误的,三角形的角平分线是三角形的内角平分线与对边相交,角的顶点与对边交点之间的线段,选项D错误.
故选D.
11.D ∵AD⊥BC,∴BC边上的高为AD,∵BA⊥AC,∴△ABC为直角三角形,∴12AC·AB=12BC·AD,即12×8×6=12×10AD,解得AD=4.8,∴BC边上的高的长为4.8.故选D.
方法解读 等积法:在一个三角形中,可以用不同的边作为底边计算面积,因为面积不变,所以能够求出某一底边上的高的长.
12.18
解析 ∵AD是△ABC的中线,∴BD=DC,∵△ACD的周长为16,∴AC+AD+CD=16,∵AC=6,∴AD+CD=166=10,∴AD+BD=10,
∴△ABD的周长为AB+BD+AD=8+10=18,故答案为18.
能力提升全练
13.B 线段CD是△ABC的AB边上的高线,故A选项说法错误,B选项说法正确;线段AD不是△ABC的BC边上的高线,故C选项说法错误;线段AD不是△ABC的AC边上的高线,故D选项说法错误.故选B.
14.D ∵AD是BC边上的中线,∴BD=DC,由题意得,(AC+CD+AD)-(AB+BD+AD)=3,∴AC-AB=3,又AC+AB=13,∴AC=8,
AB=5,故选D.
15.2
解析 ∵E是AD的中点,∴CE是△ACD的中线,∴S△ACD=2S△AEC,
∵△AEC的面积是1,∴S△ACD=2S△AEC=2,
∵AD是△ABC的中线,∴S△ABD=S△ACD=2.
方法解读 双中点模型:运用三角形的中线平分三角形的面积求图形面积,常见的双中点模型的面积关系如下:如图1,D、E分别为BC、AD的中点,则S△ACE=S△CDE=14S△ABC;如图2,D、E分别为BC、AB的中点,则S△ADE=S△BDE=14S△ABC.
图1 图2
[变式1] B ∵D是BC中点,∴S△ABD=S△ACD=12S△ABC=10,∵E是AD中点,∴S△EBD=12S△ABD=5,S△ECD=12S△ACD=5,∴S△BCE=S△EBD+S△ECD=10,故选B.
[变式2] D ∵EF=2BF,S△BCF=2 cm2,∴S△BEC=3S△BCF=3×2=6 cm2,∵D是BC的中点,∴S△BDE=S△CDE=12S△BEC=3 cm2,又∵E是AD的中点,∴S△ACD=S△ABD=2S△BDE=6 cm2,∴S△ABC=2S△ABD=12 cm2,故选D.
[变式3] A ∵D为BC的中点,∴S△ABD=S△ACD=12S△ABC,∵E,F分别是AD,AC的中点,∴S△BDE=12S△ABD,S△ADF=12S△ADC,S△DEF=12S△ADF,∴S△BDE=14S△ABC,S△DEF=14S△ADC=18S△ABC,∴S△BDE+S△DEF=14S△ABC+18S△ABC=38S△ABC,∴S△ABC=83S阴影部分=83×9=24.故选A.
16.解析 (1)在△ABC中,∠C=90°,AC=8 cm,BC=6 cm,AB=10 cm,∴△ABC的周长=8+6+10=24(cm),当CP把△ABC分成周长相等的两部分时,点P运动的路程=12×△ABC的周长,即2t=12×24,解得t=6,∴当t=6时,CP把△ABC分成周长相等的两部分.
(2)当CP把△ABC分成面积相等的两部分时,CP是△ABC的一条中线,即点P是AB的中点,此时点P运动的路程=AC+12AB=8+5=13(cm),即2t=13,解得t=132,∴当t=132时,CP把△ABC分成面积相等的两部分.
素养探究全练
17.C ∵AP1为△ABC的中线,∴S△AP1C=12S△ABC=12S,∵AP2为△AP1C的中线,∴S△AP2C=12S△AP1C=122S,∵AP3为△AP2C的中线,∴S△AP3C=12S△AP2C=123S,……,按此规律,∵APn为△APn-1C的中线,∴△APnC的面积为S2n,故选C.
18.解析 (1)3;5;7;13.
(2)∵题图②中有3个三角形,3=2×2-1,题图③中有5个三角形,5=2×3-1,题图④中有7个三角形,7=2×4-1,∴题图中有(2n-1)个三角形.
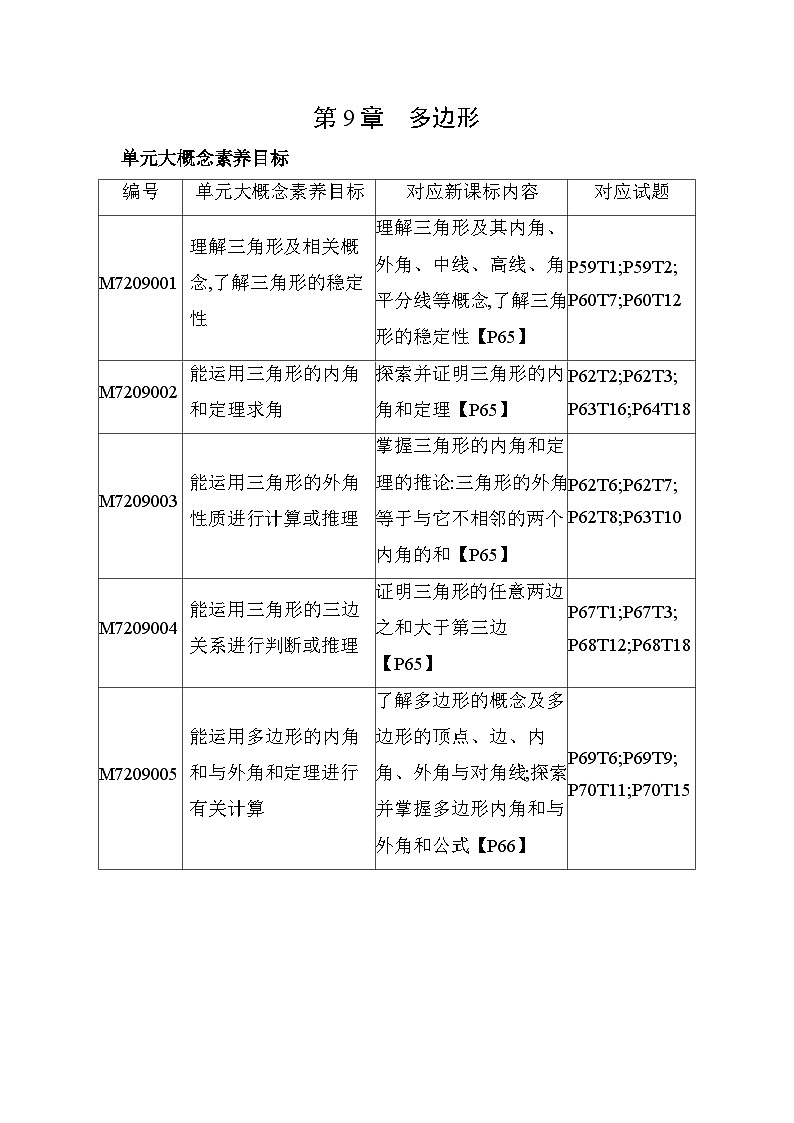
编号
单元大概念素养目标
对应新课标内容
对应试题
M7209001
理解三角形及相关概念,了解三角形的稳定性
理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性【P65】
P59T1;P59T2;
P60T7;P60T12
M7209002
能运用三角形的内角和定理求角
探索并证明三角形的内角和定理【P65】
P62T2;P62T3;
P63T16;P64T18
M7209003
能运用三角形的外角性质进行计算或推理
掌握三角形的内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和【P65】
P62T6;P62T7;
P62T8;P63T10
M7209004
能运用三角形的三边关系进行判断或推理
证明三角形的任意两边之和大于第三边【P65】
P67T1;P67T3;
P68T12;P68T18
M7209005
能运用多边形的内角和与外角和定理进行有关计算
了解多边形的概念及多边形的顶点、边、内角、外角与对角线;探索并掌握多边形内角和与外角和公式【P66】
P69T6;P69T9;
P70T11;P70T15