2024年中考数学复习课件---微专题8 解直角三角形的应用模型

这是一份2024年中考数学复习课件---微专题8 解直角三角形的应用模型，共16页。PPT课件主要包含了类型清单，模型展示，①③④，ABAD-BD，DCDE+CE等内容，欢迎下载使用。

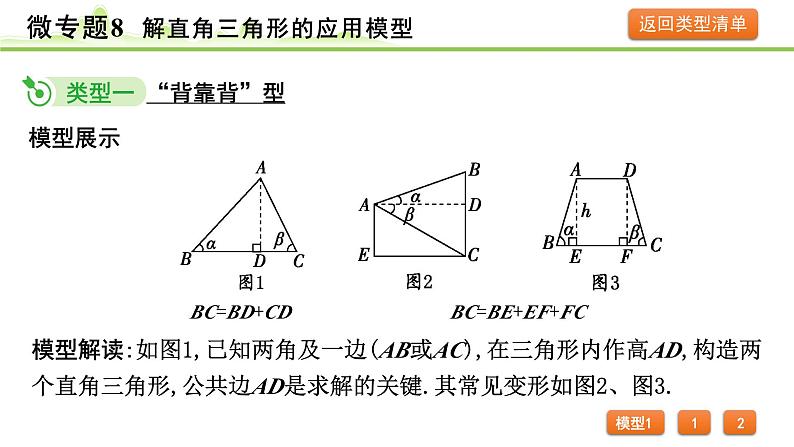
模型解读:如图1,已知两角及一边(AB或AC),在三角形内作高AD,构造两个直角三角形,公共边AD是求解的关键.其常见变形如图2、图3.
BC=BD+CD　　　 BC=BE+EF+FC
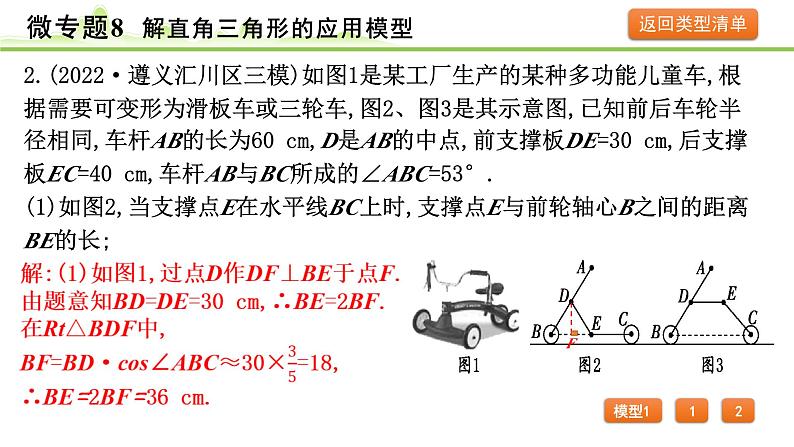
2.(2022·遵义汇川区三模)如图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2、图3是其示意图,已知前后车轮半径相同,车杆AB的长为60 cm,D是AB的中点,前支撑板DE=30 cm,后支撑板EC=40 cm,车杆AB与BC所成的∠ABC=53°.(1)如图2,当支撑点E在水平线BC上时,支撑点E与前轮轴心B之间的距离BE的长;
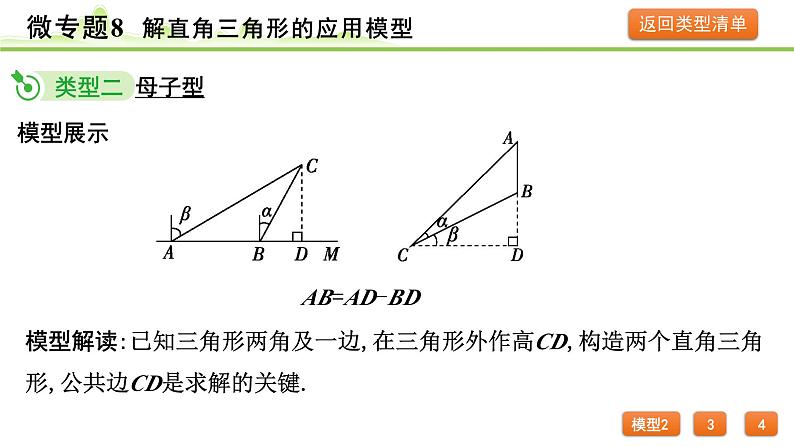
模型解读:已知三角形两角及一边,在三角形外作高CD,构造两个直角三角形,公共边CD是求解的关键.
4.(2022·遵义20题12分)如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2,AB是灯杆,CD是灯管支架,灯管支架CD与灯杆间的夹角∠BDC=60°.综合实践小组的同学想知道灯管支架CD的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得AE=3 m,EF=8 m(点A,E,F在同一条直线上).根据以上数据,解答下列问题:(1)求灯管支架底部距地面高度AD的长;(结果保留根号)
模型解读:已知两直角三角形及各自一锐角,设未知数,分别解每个直角三角形,再利用线段和差构造方程求解.
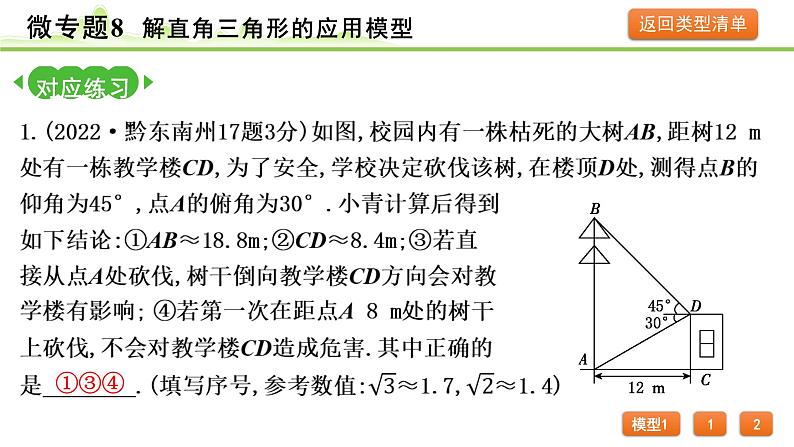
5.(2022·铜仁一模)如图,某商家想在商场大楼上悬挂一块广告牌,广告牌高AB=2 m.根据商场规定广告牌最高点不得高于地面20 m.经测量,测角仪支架高GH=CE=DF=1 m,在F处测得广告牌底部点B的仰角为30°,在E处测得广告牌顶部点A的仰角为45°,EF=12 m.请计算说明,商家这样放广告牌是否符合规定?(图中点A,B,C,D,E,F,G,H在同一平面内)
模型解读:过点B作BE⊥CD,构造直角三角形和矩形,设未知数,并解直角三角形,再通过线段和差构造方程求解.
A.12.5 mB.12.3 mC.12.2 mD.11.8 m
7.(2022·六盘水21题10分)“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,AC=AD=2 m,BF=3 m.(1)天晴时打开“天幕”,若∠α=65°,求遮阳宽度CD(结果精确到0.1 m);