


2024年中考数学复习课件---微专题4 全等模型
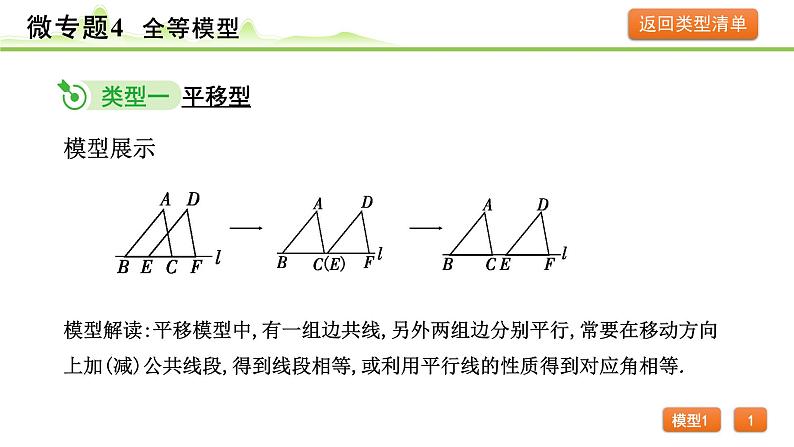
展开模型解读:平移模型中,有一组边共线,另外两组边分别平行,常要在移动方向上加(减)公共线段,得到线段相等,或利用平行线的性质得到对应角相等.
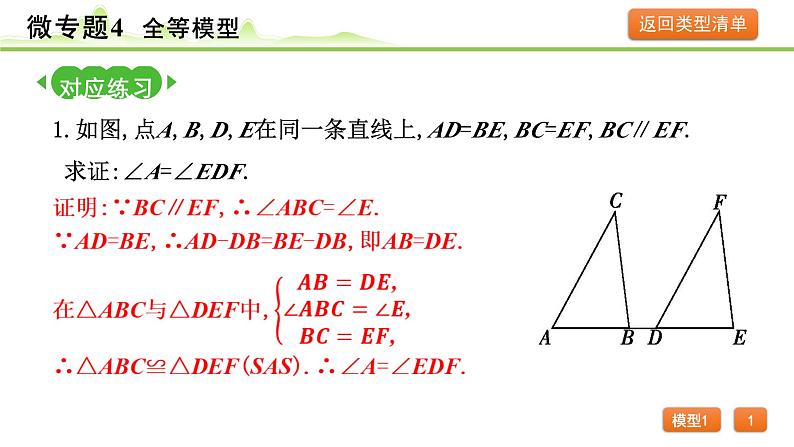
1.如图,点A,B,D,E在同一条直线上,AD=BE,BC=EF,BC∥EF. 求证:∠A=∠EDF.
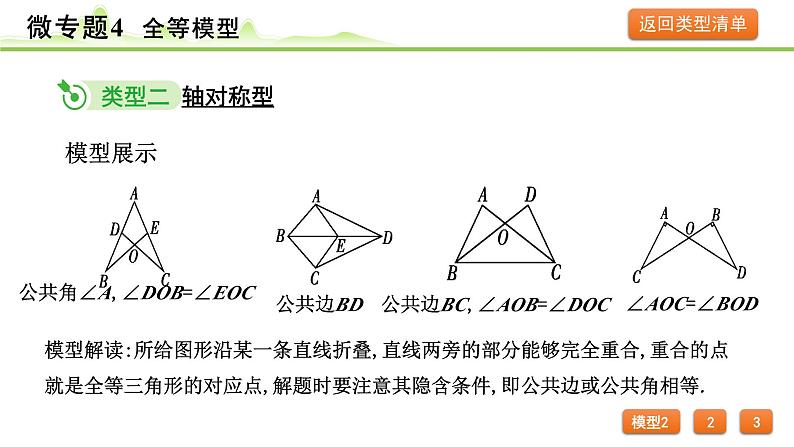
公共角∠A,∠DOB=∠EOC
公共边BC,∠AOB=∠DOC
模型解读:所给图形沿某一条直线折叠,直线两旁的部分能够完全重合,重合的点就是全等三角形的对应点,解题时要注意其隐含条件,即公共边或公共角相等.
2.如图,D,E分别是AB,AC的中点,BE,CD相交于点O,∠B=∠C,BD=CE. 求证:(1)OD=OE;
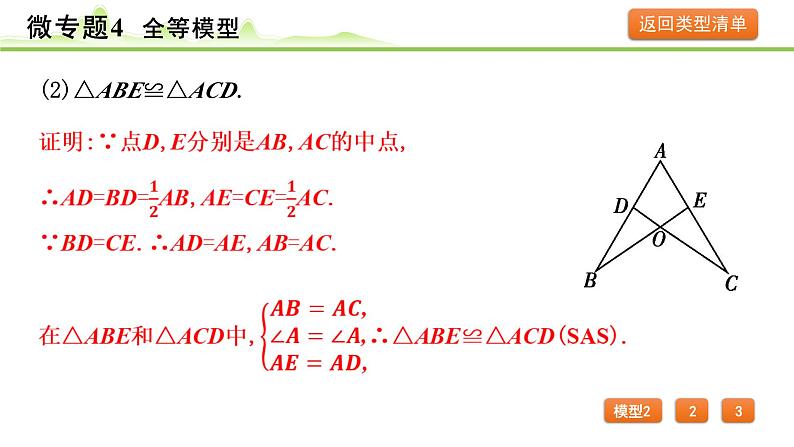
(2)△ABE≌△ACD.
3.(2022·铜仁玉屏县一模)如图,在△ABC中,AB=AC,D是BC的中点,连 接AD,在AD的延长线上取一点E,连接BE,CE. 求证:△ABE≌△ACE.
证明:∵AB=AC,点D为BC的中点,∴∠BAE=∠CAE.又∵AE=AE,∴△ABE≌△ACE(SAS).
等角∠ACB=∠DCE
利用角度 的和或差
模型解读:此模型可看成是将三角形绕着公共顶点旋转一定角度所构成的.
4.如图,△ACB和△DCE均为等边三角形,点D和点E分别位于边BC的两侧, 连接AD,BE. (1)求证:AD=BE;
(2)当点A,D,E在同一直线上时,求∠DEB的度数.
解:∵△CDE是等边三角形,∴∠CDE=∠CED=60°.当点A,D,E在同一直线上时,∠ADC+∠CDE=180°,∴∠ADC=120°. ∵△ACD≌△BCE,∴∠BEC=∠ADC=120°,∴∠DEB=∠BEC-∠CED=120°-60°=60°.
模型解读:在“一线三等角”模型中,两个三角形的对应角相等,只需找出一组对应边相等,就可以得出这两个三角形全等.
5.如图,∠BAC=90°,AB=AC,BE⊥AD于点E,CF⊥AD于点F,求证: AF=BE.
中考数学复习重难突破微专题(五)半角模型课件: 这是一份中考数学复习重难突破微专题(五)半角模型课件,共15页。
中考数学复习微专题一常考的四大全等模型模型四旋转模型(手拉手模型)课件: 这是一份中考数学复习微专题一常考的四大全等模型模型四旋转模型(手拉手模型)课件,共8页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
中考数学复习微专题一常考的四大全等模型模型三三垂直模型(一线三直角)课件: 这是一份中考数学复习微专题一常考的四大全等模型模型三三垂直模型(一线三直角)课件,共8页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。












