内蒙古包头市青山区2024届九年级上学期期末考试数学试卷(含答案)

这是一份内蒙古包头市青山区2024届九年级上学期期末考试数学试卷(含答案)，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．一元二次方程的两实数根相等，则a的值为( ).
A.B.或C.D.或
2．在中，，若斜边AB是直角边BC的3倍，则的值是( )
A.B.3C.D.
3．如图，以点O为位似中心，将放大后得到，，，则与的面积比为( )
A.B.C.D.
4．有长度分别为2cm，3cm，4cm，7cm的四条线段，任取其中三条能组成三角形的概率是( ).
A.B.C.D.
5．将抛物线向下平移1个单位长度，再向左平移2个单位长度后，得到的抛物线表达式是( )
A.B.C.D.
6．一个等腰三角形的两条边长分别是方程的两根，则该等腰三角形的周长是( )
A.4.8B.10C.12D.8或10
7．如图，为的直径，点C是弧的中点.过点C作于点G，交于点D，若，，则的半径长是( )
A.5B.6.5C.7.5D.8
8．2011广州大运会的某纪念品原价100元，连续两次降价后售价为81元，a的值是( )
A.B.C.D.
9．如图，是等腰直角三角形，，，点D为边上一点，过点D作，，垂足分别为E，F，点D从点A出发沿运动至点B.设，，四边形的面积为S，在运动过程中，下列说法正确的是( )
A.y与x满足一次函数关系，S与x满足二次函数关系，且S存在最大值
B.y与x满足一次函数关系，S与x满足二次函数关系，且S存在最小值
C.y与x满足反比例函数关系，S与x满足二次函数关系，且S存在最大值
D.y与x满足反比例函数关系，S与x满足二次函数关系，且S存在最小值
10．如图，在矩形中，，点E，F分别在，边上，，，AF与相交于点O，连接，若，则与之间的数量关系正确的是( )
A.B.C.D.
二、填空题
11．若，则______.
12．在一个不透明的袋中装有黑色和红色两种颜色的球共15个，每个球除颜色外都相同，每次摇匀后随即摸出一个球，记下颜色后再放回袋中，通过大量重复摸球实验后，发现摸到黑球的频率稳定于，则可估计这个袋中红球的个数约为______.
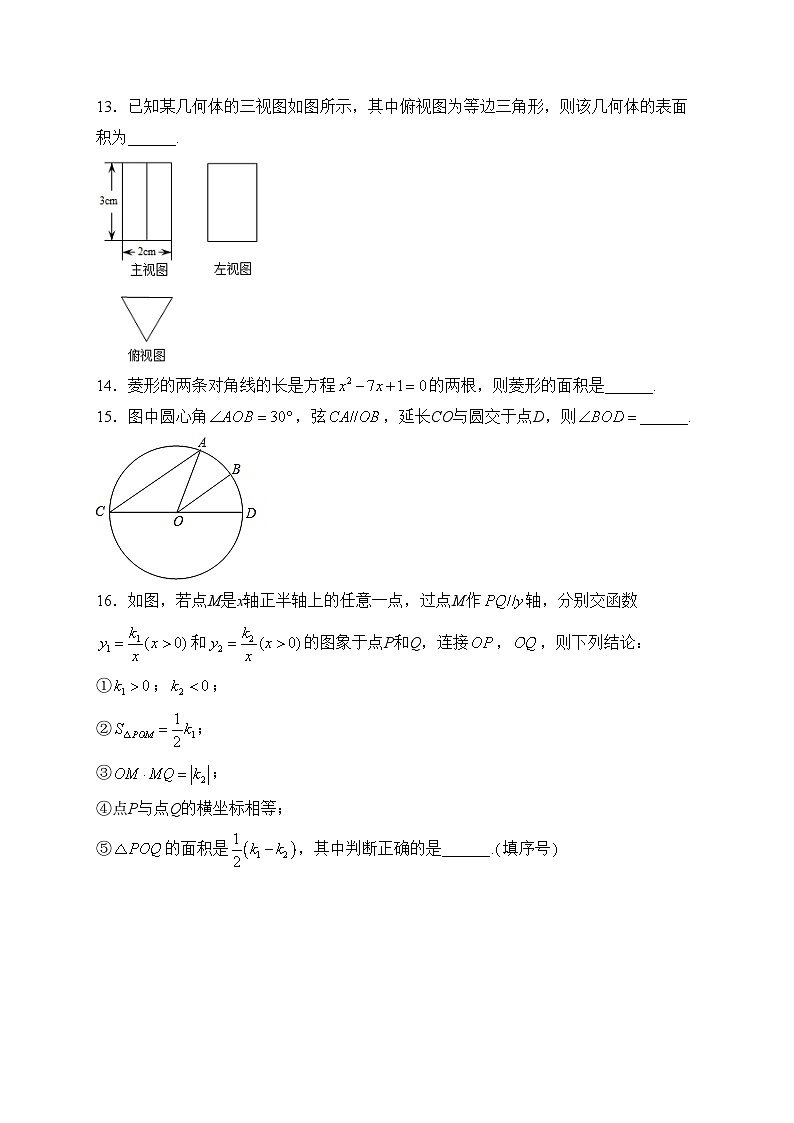
13．已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积为______.
14．菱形的两条对角线的长是方程的两根，则菱形的面积是______.
15．图中圆心角，弦，延长CO与圆交于点D，则______.
16．如图，若点M是x轴正半轴上的任意一点，过点M作轴，分别交函数和的图象于点P和Q，连接，，则下列结论：
①；；
②；
③；
④点P与点Q的横坐标相等；
⑤的面积是，其中判断正确的是______填序号
三、解答题
17．计算：
18．用配方法解方程：.
19．甲、乙两个不透明的盒子里分别装有3张卡片，其中甲盒里3张卡片分别标有数字1、2、3；乙盒里3张卡片分别标有数字4、5、6.这些卡片除数字外其余都相同，将卡片充分摇匀.
（1）从甲盒里随机抽取一张卡片，求抽到的卡片上标有数字为偶数的概率；
（2）从甲盒、乙盆里各随机描取一张卡片，请用列表或树状图的方法，求抽到的两张卡片上标有数字之和不大于7的概率.
20．小明开着汽车在平坦的公路上行驶，前放出现两座建筑物A、B（如图），在（1）处小颖能看到B建筑物的一部分，（如图），此时，小明的视角为30°，已知A建筑物高25米.
（1）请问汽车行驶到什么位置时，小明刚好看不到建筑物B？请在图中标出这点.
（2）若小明刚好看不到B建筑物时，他的视线与公路的夹角为45°，请问他向前行驶了多少米？（精确到0.1）
21．某公司今年国庆期间在网络平台上进行直播销售猕猴桃，已知猕猴桃的成本价格为8元/kg，经销售发现：每日销售量与销售单价x（元/kg）满足一次函数关系，下表记录的是有关数据，销售单价不低于成本价且不高于24元/kg.设公司销售猕猴桃的日获利为w（元）.
（1）请求出日销售量y与销售单价x之间的函数关系式；
（2）当销售单价定为多少时，销售这种猕猴桃日获利w最大？最大利润为多少元？
22．如图，一次函数的图象与反比例函数的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知点A坐标为，点B的坐标为
（1）求反比例函数的解析式和一次函数的解析式；
（2）观察图象直接写出时x的取值范围是______ .
（3）直接写出：P为x轴上一动点，当三角形为等腰三角形时点P的坐标______ .
23．（1）问题发现：
如图1，在正方形中，点E，F，G，H分别在边，，，上，且，则______；
（2）类比探究：
如图2，在（1）的条件下，把“正方形”改为“矩形，且，”其它条件不变，则______，证明你的结论；
（3）拓展应用：
如图3，在中，，，，点D为的中点，连接，点E为上一点，，则______.
24．如图，三角形是以为底边的等腰三角形，点A、C分别是一次函数的图象与y轴、x轴的交点，点B在二次函数的图象上，且该二次函数图象上存在一点D使四边形能构成平行四边形.
（1）求B、D坐标，并写出该二次函数表达式；
（2）动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：
①当P运动到何处时，有？
②当P运动到何处时，四边形的面积最小？此时四边形的面积是多少？
参考答案
1．答案：B
解析：因为方程有两相等的实数根，，解得.
故选：B.
2．答案：D
解析：设，则，
由勾股定理得，，
，
故选：D.
3．答案：D
解析：以点O为位似中心，将放大后得到，
，
.
故选：D.
4．答案：D
解析：长度为2cm、3cm、4cm、7cm的四条线段，从中任取三条线段共有2.3.4，2.3.7，3.4.7，2.4.7四种情况，而能组成三角形的有2、3、4；共有1种情况，
能组成三角形的概率是.
故选D.
5．答案：C
解析：因为.
所以将抛物线先向下平移1个单位长度，再向左平移2个单位长度后，得到的抛物线的表达式为，即.
故选：C.
6．答案：B
解析：解方程得
，，
①等腰三角形的三边是2，2，4
，
不符合三角形三边关系定理，不符合题意，舍去；
②等腰三角形的三边是2，4，4，此时符合三角形三边关系定理，三角形的周长是；
即等腰三角形的周长是10.
故选：B.
7．答案：A
解析：连接，如图，设的半径为r，
，
，，
点C是弧BE的中点，
，
，
，
，
在中，
，，
，解得，
即的半径为5.
故选：A.
8．答案：B
解析：根据题意列方程得
，
解得，（不符合题意，舍去）
这两次降价，即.
故选：B.
9．答案：A
解析：是等腰直角三角形，，
，
，，
和是等腰直角三角形，四边形是矩形，
，，
，
即，
y与x满足一次函数关系，
，最大值为1，
S与x满足二次函数关系，且S存在最大值.
故选：A.
10．答案：A
解析：过点O作于点M，
，
四边形ABCD是矩形，
，

，
，
四边形ABFE是矩形，
又，
四边形ABFE是正方形，
，，，
，
，
，，
由勾股定理得，
，
故选：A.
11．答案：
解析：，
.
故答案为：.
12．答案：
解析：黑球个数为：，红球个数：.
故答案为6.
13．答案：
解析：该几何体是一个三棱柱，底面等边三角形边长为，高为，三棱柱的高为，
所以其表面积为
故答案为.
14．答案：
解析：设方程的两个根为a，b，
则由根与系数的关系得：，
菱形的两条对角线的长是方程的两根，
菱形的对角线的积为1，
菱形的面积是，
故答案为.
15．答案：30°
解析：，，
.
，
.
和是同弧所对的圆周角和圆心角，
.
.
故答案为：30°.
16．答案：①②③④⑤
解析：函数在第一象限，的图象位于第四象限，
；，故①正确；
由反比例函数系数k的几何意义，，，
，即；故②③正确；
轴，
点P与点Q的横坐标相等，故④正确；
，，
⑤的面积，故⑤正确，
故答案为：①②③④⑤.
17．答案：
解析：
.
18．答案：，
解析：，
原方程化为，
配方得，
即，
开方得，
，
，.
19．答案：（1）抽到的卡片上标有数字为偶数的概率为
（2）抽到的两张卡片上标有数字之和不大于7的概率为
解析：（1）甲盒里随机抽取一张卡，抽到的卡片上标有数字为偶数的概率是；
（2）根据题意可列表格如下：
总共有9种结果，每种结果出现的可能性相同，其中两张卡片数字之和不大于7的有六种：，，，，，，
.
20．答案：（1）汽车行驶到E点位置时，小明刚好看不到建筑物B
（2）他向前行驶了18.3米
解析：（1）如图所示：
汽车行驶到E点位置时，小明刚好看不到建筑物B；
（2）小明的视角为30°，A建筑物高25米，
，
，
，
，
，
.
则他向前行驶了18.3米.
21．答案：（1）
（2）当销售单价定为19元时，销售这种猕猴桃最大利润为12100元
解析：（1）设y与x之间的函数关系式为，
把和代入得：
，
解得，
y与x之间的函数关系式为；
（2）由题意得：
，
，
当时，w有最大值，最大值为12100，
当销售单价定为19元时，销售这种猕猴桃日获利w最大，最大利润为12100元.
22．答案：（1）；
（2）或
（3）或或或
解析：（1）点A坐标为，
把点A的坐标代入得：，
反比例函数的解析式是；
把点B的坐标为代入得：
，
解得：，
；
把A、B两点的坐标代入中得：
，
解得：，
一次函数的解析式为：；
（2）如图，由图象得：时x的取值范围是：或；
（3）当是等腰三角形时，存在以下三种情况：
①当时，如图2，
，
，
或；
②当时，如图3，
；
③当时，如图4，过A作轴于E，
设，则，，
，
，
，
；
综上，P的坐标为或或或.
故答案为：或或或.
23．答案：（1）1；
（2），见解析
（3）
解析：（1）作交BC于M，作交AB于N，
则，，，
，
，
又，，
，
；
；
，
故答案为：1；
（2）；
证明：过点E作于点M，过点H作于点N，设与的交点为O，
，
，
又因为，
；
又；
；
又，；
（3）.
如图，
将补成矩形，延长交于点G，
由已知条件可得，，
由（2）得：，
，
，
又，
，即，
.
24．答案：（1）；；
（2）当点P运动到距离A点个单位处时，四边形面积最小，最小值为
解析：（1）由，
令，得，所以点；
令，得，所以点，
是以为底边的等腰三角形，
B点坐标为，
又四边形是平行四边形，
D点坐标为，
将点、点代入二次函数得：
，
解得：，
故该二次函数解析式为：.
（2），，
.
①设点P运动了t秒时，，如图，此时，，，
，
，，
，
，即，
解得：.
即当点P运动到距离A点个单位长度处，有.
②，且，
当的面积最大时，四边形的面积最小，
当动点P运动t秒时，，，，
设底边上的高为h，作于点H，
由可得：，
解得：，
，
当时，达到最大值，
此时，
故当点运动到距离A点个单位处时，四边形面积最小，最小值为.
x（元/kg）
9
10
11
2100
2000
1900
4
5
6
1
2
3