




重庆市梁平区梁平区福德学校2023-2024学年七年级下学期第一次月考数学试题(原卷版+解析版)
展开一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填在下表相应的空格中.
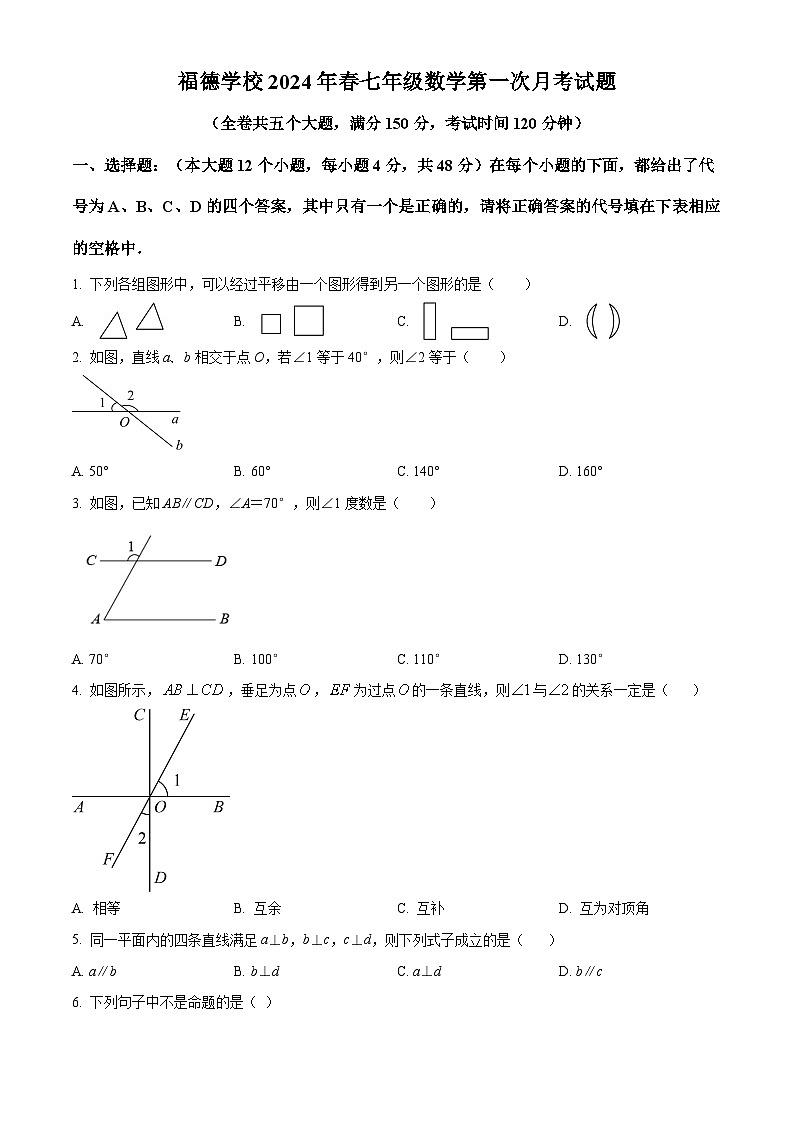
1. 下列各组图形中,可以经过平移由一个图形得到另一个图形的是( )
A. B. C. D.
2. 如图,直线a、b相交于点O,若∠1等于40°,则∠2等于( )
A. 50°B. 60°C. 140°D. 160°
3. 如图,已知AB∥CD,∠A=70°,则∠1度数是( )
A. 70°B. 100°C. 110°D. 130°
4. 如图所示,,垂足为点,为过点的一条直线,则与的关系一定是( )
A. 相等B. 互余C. 互补D. 互为对顶角
5. 同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A. a∥bB. b⊥dC. a⊥dD. b∥c
6. 下列句子中不是命题的是( )
A 两直线平行,同位角相等B. 直线AB垂直于CD吗?
C. 若|a|=|b|,则a2=b2D. 同角的补角相等
7. 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A. 先把△ABC向左平移5个单位,再向下平移2个单位
B. 先把△ABC向右平移5个单位,再向下平移2个单位
C. 先把△ABC向左平移5个单位,再向上平移2个单位
D 先把△ABC向右平移5个单位,再向上平移2个单位
8. 如图,点在的延长线上,下列条件中能判断的是( ).
A. B.
C. D.
9. 实数a,b在数轴上的位置,如图所示,那么化简的结果是
A. B. bC. D.
10. 若,则 ( )
A. B. C. D. 或
11. 在下列数中,无理数的个数( )
,,,,3.1415,,,,
A. 3个B. 4个C. 5个D. 6个
12. 在下列说法中:①10的平方根是;②是4的一个平方根;③的平方根是;④的算术平方根是,其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将正确答案直接填在题后的横线上.
13. 绝对值等于的数是:______,的相反数是:______.
14. 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=25°,则∠2的度数等于_____________.
15 已知=____________
16. 比较下列各组数的大小:
(1)______
(2)______.
17. 若整数部分为a,的整数部分为b,则______.
18. 已知图为长是5、宽是3的矩形,空白部分为两条宽1的道路,阴影部分为草坪,则阴影部分的面积为______.
三、解答题:(本大题2个小题,19题8分,20题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤.
19. 计算:
(1)
(2)
20. 计算:
(1)
(2)
四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.
21. 已知一个正数的两个平方根分别为2a+5和3a-15.
(1)求这个正数;
(2)请估算30a的算术平方根在哪两个连续整数之间
22. 完成下面推理过程:如图,已知,,推得.
理由如下:
∵(已知),
且( ),
∴(等量代换).
∴( ).
∴ ( ).
又∵(已知),
∴ (等量代换).
∴( ).
23. 如图,,直线分别交、于点、,平分,若,求的度数.
24. 已知:如图,,.求证:.
五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)必须给出必要的演算过程或推理步骤.
25. 如图已知,把一张长方形纸片沿折叠后与的交点为G,D、C分别在M、N的位置上.若,求和的度数.
26. 类比平方根(二次方根)、立方根(三次方根)的定义可给出四次方根、五次方根的定义:
①如果,那么x叫做a四次方根;
②如果,那么x叫做a的五次方根;
请根据以上两个定义并结合有关数学知识回答问题:
(1)81的四次方根为______;的五次方根为______.
(2)若有意义,则a的取值范围为______;若有意义,则a的取值范围为______.
(3)解方程:
①
②
13,重庆市梁平区2023-2024学年七年级上学期期末数学试题: 这是一份13,重庆市梁平区2023-2024学年七年级上学期期末数学试题,共16页。试卷主要包含了每月用水量等内容,欢迎下载使用。
重庆市梁平区梁平区袁驿中学2023-2024学年九年级上学期期中数学试题(原卷+解析): 这是一份重庆市梁平区梁平区袁驿中学2023-2024学年九年级上学期期中数学试题(原卷+解析),文件包含精品解析重庆市梁平区梁平区袁驿中学2023-2024学年九年级上学期期中数学试题原卷版docx、精品解析重庆市梁平区梁平区袁驿中学2023-2024学年九年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
重庆市梁平区2022-2023学年八年级下学期期末数学试题(解析版): 这是一份重庆市梁平区2022-2023学年八年级下学期期末数学试题(解析版),共24页。












