2024年中考数学复习课件---第8讲 一元二次方程及其应用

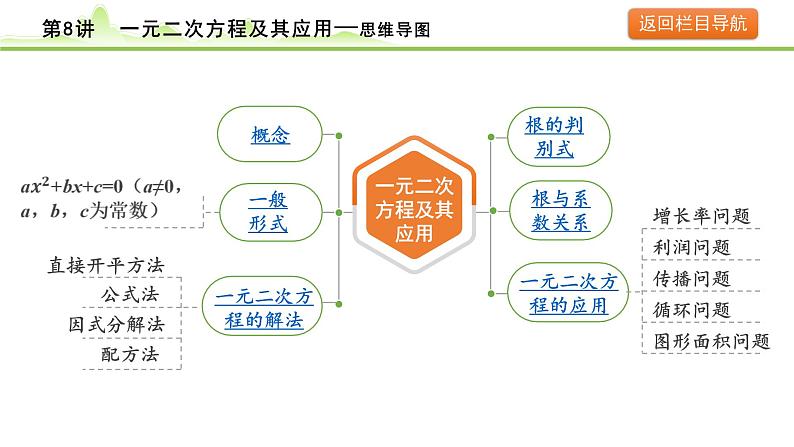
这是一份2024年中考数学复习课件---第8讲 一元二次方程及其应用，共43页。PPT课件主要包含了栏目导航，一元二次方程及其应用，一般形式，一元二次方程的解法，直接开平方法，公式法，因式分解法，配方法，增长率问题，利润问题等内容，欢迎下载使用。
1. 理解配方法,能用配方法、公式法、因式分解法解数字系数的一元 二次方程.2. 会用一元二次方程根的判别式判别方程是否有实根及两个实根是否 相等.3. 了解一元二次方程的根与系数的关系.
4. 能根据现实情境理解方程的意义,能针对具体问题列出方程;理解方 程解的意义.5. 能根据具体问题的实际意义,检验方程解的合理性.
教材链接人教:九上P1~P26　北师:九上P30~P58　湘教:九上P25~P58
概念：只含有一个未知数并且未知数的最高次数是①_______的整式方程，叫 做一元二次方程.
【易错提示】对于二次项系数含有字母的方程，根据根的情况求字母的取值范 围时，一定要先确定该方程式一元二次方程还是一元一次方程， 再进行判断. 
设a为原来量，变化后的量为b,变化次数为2，当平均增长率为x时，有⑨__________；当平均下降率为x时，则有⑩_______
传播问题：设每轮传播中每个人传染x个人，则两轮传播后感染的总人数为 ⑪__________
单循环淘汰赛问题：设x个队进行m场比赛，则m=⑫__________（x≥2）
互赠照片问题：设全班x人，每人向其他人赠送一张自己的照片，全班共送了m张照片，则m=⑬________（x≥2）
（1）如图1，设空白部分的宽均为x，则S阴影=⑭__________
（2）如图2，图3，图4，设空白部分的宽均为x，则S阴影=, ⑮ __________
(a-2x)(b-2x)
一元二次方程的解法及根的判别式
例1 核心素养·运算能力 (2022·贵阳观山湖区一模)已知方程 x2-3x+k=0是关于x的一元二次方程. (1)当k=2时,求该一元二次方程的根;
解:(1)把k=2代入,得x2-3x+2=0, 分解因式,得(x-1)(x-2)=0, ∴x-1=0或x-2=0, 解得x1=1,x2=2.
(2)若该一元二次方程无实数根,请计算后写出一个满足条件的k值.
方法指导(1)根据方程系数,灵活选择解方程的方法:①没有一次项,直接开平方;②二次项系数为1,宜用配方法;③无常数项,因式分解最简便;④无明显特征,用公式法.(2)依据有无实数根,得出判别式与0的关系,从而推算字母参数的取值范围.
1.(2022·毕节模拟)已知等腰三角形的腰和底的长分别是一元二次方 程x2-6x+8=0的根,则该三角形的周长为 (　　) A.8　　B.10　　 C.8或10　　D.12
例2 某大型果品批发商场经销一种高档坚果,进价每千克33元,原售价 每千克64元,连续两次降价后每千克49元. (1)若每次下降的百分率相同,求每次下降的百分率;
解:(1)设每次下降的百分率为a,根据题意,得 64(1-a)2=49,解得a1=1.875(舍去),a2=0.125=12.5%. 答:每次下降的百分率为12.5%.　
(2)两次降价后,每天可售出160千克.经市场调查发现,在进货价不变的情况下,若每千克降价3元,日销售量将增加120千克.现该商场要保证销售该坚果每天盈利3 640元,又要尽可能让顾客得到实惠,求这种坚果的售价应定为每千克多少元.
方法指导1.用一元二次方程解决变化率问题时,要注意增长率大于0,降低率大于0且小于1.2.明确经济类问题的等量关系通常为“单件利润×数量=总利润”.3.分析数量关系时,可以列表分析问题中价格变化前后的单件利润、数量、总利润.
3. 改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD) 16 m,宽(AB)9 m的矩形场地ABCD上修建三条同样宽的小路,其中两 条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面 积为112 m2,则小路的宽应为　　　　m. 
4. 如图,在△ABC中,AB=6 cm,BC=7 cm,∠ABC=30°,点P从A点出发, 以1 cm/s的速度向B点移动,点Q从B点出发,以2 cm/s的速度向C点移 动,当其中一个动点到达终点时,另一动点也随之停止运动.
如果P,Q两点同时出发,经过几秒后,△PBQ的面积等于4 cm2?
（2017~2022）
（贵阳6年2考，毕节2020.18）
1. (2020·黔东南州8题4分)若菱形ABCD的一条对角线长为8,边CD的 长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为 (　　) A.16　　B.24　　C.16或24　　D.482. (2020·毕节18题5分)关于x的一元二次方程(k+2)x2+6x+k2+k-2=0有 一个根是0,则k的值是　　　　. 
4.(2022·贵阳17(2)题6分)在初中阶段我们已经学习了一元二次方程的 三种解法,他们分别是配方法、公式法和因式分解法,请从下列一元二 次方程中任选两个,并解这两个方程. ①x2+2x-1=0;②x2-3x=0;③x2-4x=4;④x2-4=0.
①x2+2x-1=0;②x2-3x=0;③x2-4x=4;④x2-4=0.
（遵义2017.9，毕节6年2考）
5. (2019·铜仁6题4分)一元二次方程4x2-2x-1=0的根的情况为(　　) A.有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根 D.没有实数根
6.(2020·黔西南州8题4分)已知关于x的一元二次方程(m-1)x2+2x+1=0 有实数根,则m的取值范围是(　　) A.m