



所属成套资源:【中考二轮】备战2023年中考数学《重难点解读•专项训练》(全国通用)
备战中考数学《重难点解读•专项训练》专题07 二次函数与直角三角形有关的问题(专项训练)
展开这是一份备战中考数学《重难点解读•专项训练》专题07 二次函数与直角三角形有关的问题(专项训练),文件包含专题07二次函数与直角三角形有关问题专项训练原卷版docx、专题07二次函数与直角三角形有关问题专项训练解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
专题07 二次函数与直角三角形有关问题(专项训练)
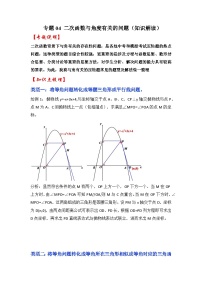
1.(2020•徐州)如图,在平面直角坐标系中,函数y=﹣ax2+2ax+3a(a>0)的图象交x轴于点A、B,交y轴于点C,它的对称轴交x轴于点E.过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE、GK.
(1)点E的坐标为: ;
(2)当△HEF是直角三角形时,求a的值;
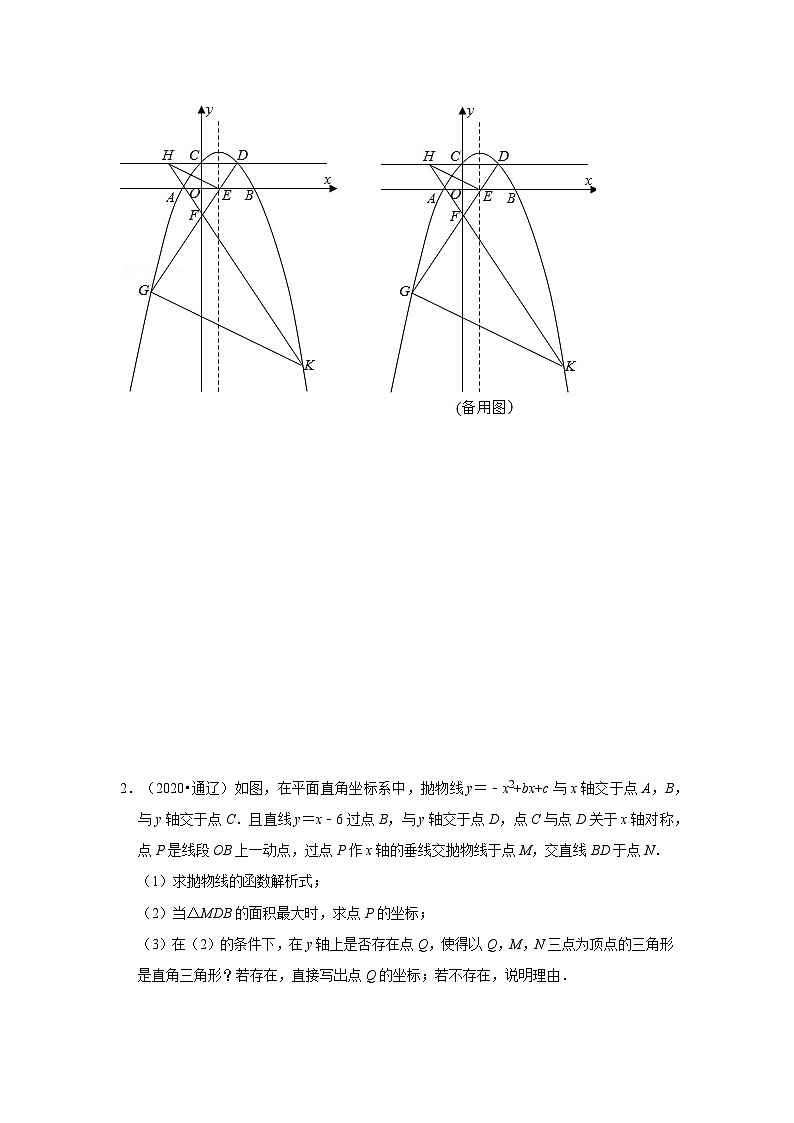
2.(2020•通辽)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C.且直线y=x﹣6过点B,与y轴交于点D,点C与点D关于x轴对称,点P是线段OB上一动点,过点P作x轴的垂线交抛物线于点M,交直线BD于点N.
(1)求抛物线的函数解析式;
(2)当△MDB的面积最大时,求点P的坐标;
(3)在(2)的条件下,在y轴上是否存在点Q,使得以Q,M,N三点为顶点的三角形是直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由.
3.(2020•广元)如图,直线y=﹣2x+10分别与x轴,y轴交于A,B两点,点C为OB的中点,抛物线y=x2+bx+c经过A,C两点.
(1)求抛物线的函数表达式;
(2)点P为抛物线上一点,若△APB是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
4.(2022•南岸区校级模拟)如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴分别交于A、B两点,与y轴交于点C,连接AC、BC,其中A(﹣2,0),C(0,6).
(1)求抛物线的解析式;
(2)点P是直线BC上方抛物线上一点,过点P作PE∥y轴交BC于点E,作PF∥x轴交BC于点F,求CF+BE的最小值,及此时点P的坐标;
(3)如图2,x轴上有一点Q(﹣1,0),将抛物线向x轴正方向平移,使得抛物线恰好经过点Q,得到新抛物线y1,点D是新抛物线y1与原抛物线的交点,点E是新抛物线y1上一动点,连接DQ,当△DQE是以DQ为直角边的直角三角形时,直接写出所有符合条件的点E的坐标.
5.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.
(1)求抛物线的解析式;
(2)当△ODF为直角三角形时,请直接写出点D的坐标.
6.(2022•雁峰区校级模拟)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴交于点C,直线y=x+1与x轴交于点E,与y轴交于点D.
(1)求抛物线的解析式;
(2)M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.
7.(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A(﹣1,0),对称轴为直线x=2.
(1)求该抛物线的表达式;
(2)直线l过点A与抛物线交于点P,当∠PAB=45°时,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
8.(2022•滕州市二模)抛物线y=﹣x2+2x+3与x轴交于A,B两点.与y轴交于点C,点D为抛物线的顶点.
(1)求A,B,C,D的坐标;
(2)点P为抛物线上的动点,当△PAC是直角三角形时,求点P的坐标;
9.(2022•市中区二模)如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C,动点P在抛物线的对称轴上.
(1)求抛物线的关系式;
(2)当以P,A,C为顶点的三角形周长最小时,求点P的坐标及△PAC的周长;
(3)若点Q是直线BC上方抛物线上一点,当△BCQ为直角三角形时,求出点Q的坐标.
相关试卷
这是一份备战中考数学《重难点解读•专项训练》专题08 二次函数与平行四边形有关问题(专项训练),文件包含专题08二次函数与平行四边形有关问题专项训练原卷版docx、专题08二次函数与平行四边形有关问题专项训练解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份备战中考数学《重难点解读•专项训练》专题05 二次函数与相似三角形有关的问题(专项训练),文件包含专题05二次函数与相似三角形有关问题专项训练原卷版docx、专题05二次函数与相似三角形有关问题专项训练解析版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
这是一份备战中考数学《重难点解读•专项训练》专题04 二次函数与角度有关的问题(专项训练),文件包含专题04二次函数与角度有关问题专项训练原卷版docx、专题04二次函数与角度有关问题专项训练解析版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。