2024春七下数学第7章一元一次不等式与不等式组集训课堂练素养1一元一次不等式组的解法技巧课件（沪科版）

这是一份2024春七下数学第7章一元一次不等式与不等式组集训课堂练素养1一元一次不等式组的解法技巧课件（沪科版），共26页。

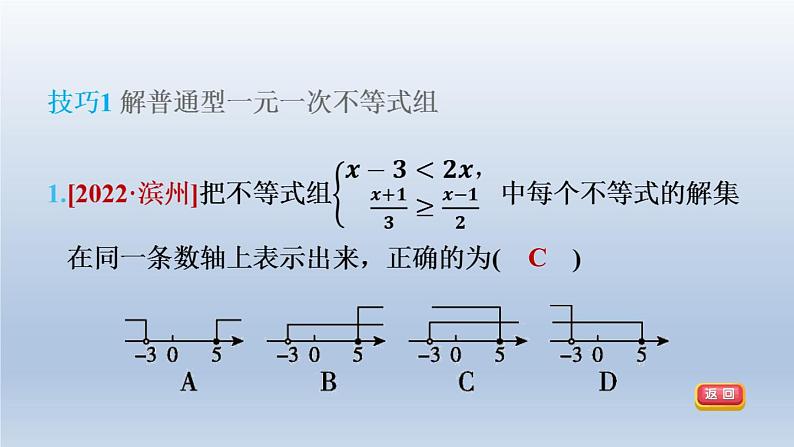
沪科版七年级下第7章　一元一次不等式与不等式组集训课堂第7章练素养　1.一元一次不等式组的解法技巧答 案 呈 现习题链接CBD1.求一元一次不等式组的解集就是求不等式组中几个不等式解集的公共部分，当几个不等式的解集没有公共部分时，我们通常说这个不等式组无解.2.确定一元一次不等式组解集的常用方法：(1)数轴法；(2)口诀法. C D【点拨】利用数轴找不等式组整数解的步骤：(1)解不等式组；(2)将不等式组的解集在数轴上表示出来；(3)观察解集在数轴上的范围；(4)确定其整数解. 【解】解不等式①，得x＞－1，解不等式②，得x＜3.在数轴上表示不等式①、②的解集如下：所以原不等式组的解集是－1＜x＜3，所以它的所有整数解有0，1，2.  解不等式①，得x＞－1；解不等式②，得x≤8，所以原不等式组的解集为－1＜x≤8.  B【点拨】   解不等式①，得x≥4－2a； 解得a＝2，b＝－1.  解这两个不等式组，得0≤x＜3或－3＜x＜0.故｜x｜＜3的解集为－3＜x＜3.根据以上材料，解答下列问题：(1)解不等式：｜2x－1｜＜3.  (2)解不等式：x＋｜2x－1｜＞3. (3)解不等式｜x｜＋｜2x－1｜＜3时需化成几个不等式组？解出该不等式.      所以分式不等式可转化为下面两个不等式组：    (2)化简：｜－4a＋5｜－｜a＋4｜.【解】由(1)知－4a＋5＞0且a＋4＞0，所以原式＝－4a＋5－a－4＝－5a＋1. 【解】满足题意的所有整数a的和是15.