人教版数学九年级上册 25.1随机事件与概率课时2课件

这是一份人教版数学九年级上册 25.1随机事件与概率课时2课件，共25页。

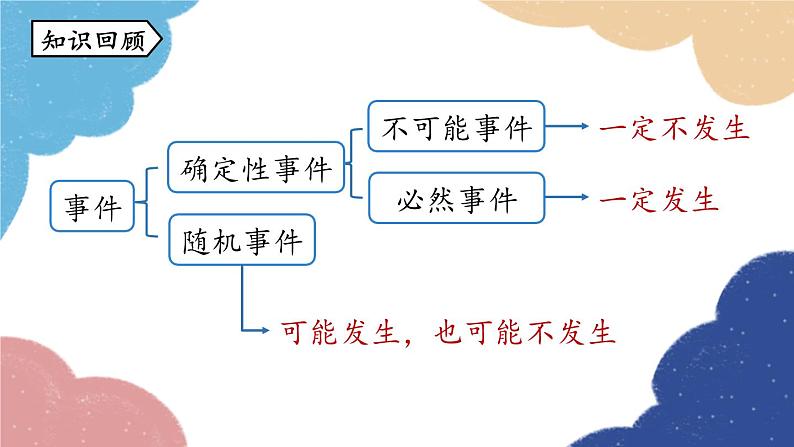
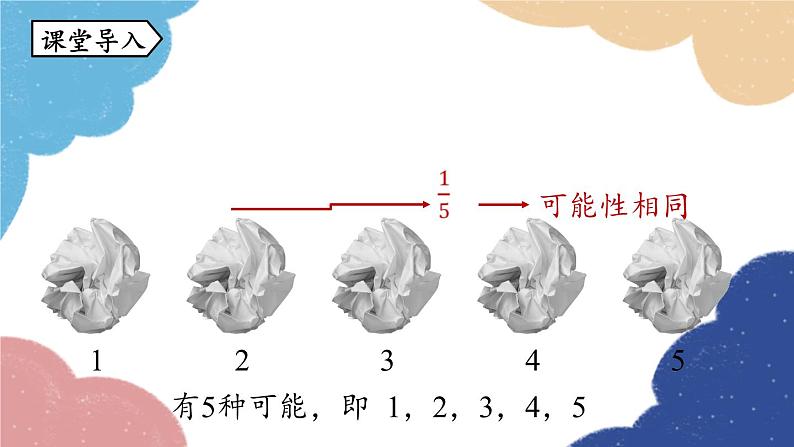
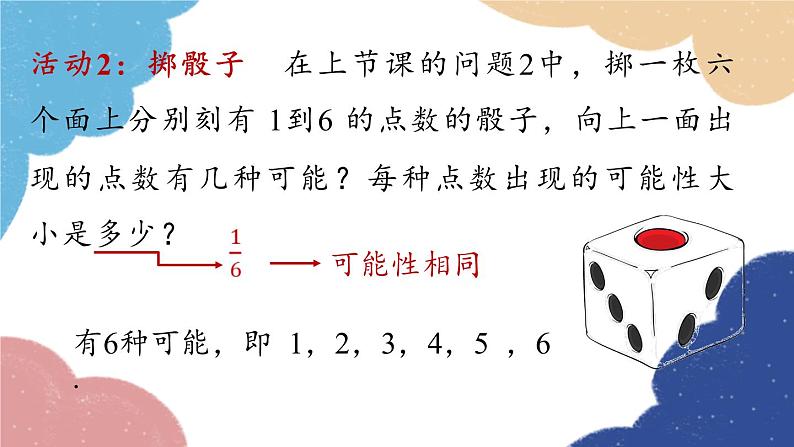
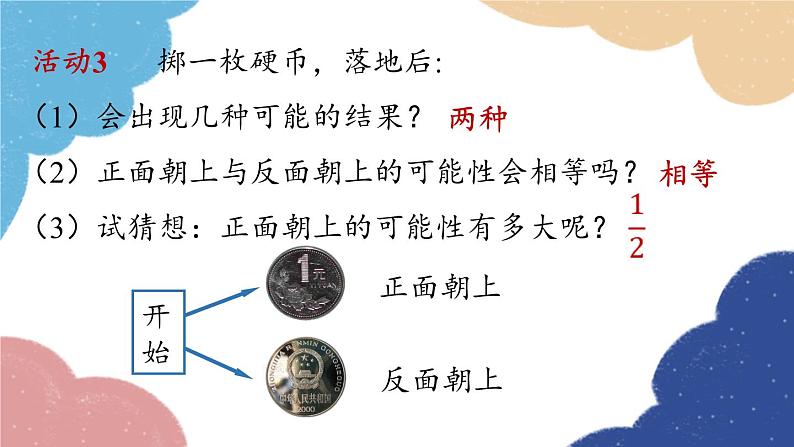
25.1.2 概率随机事件与概率九年级上册 RJ初中数学不可能事件必然事件确定性事件随机事件事件知识回顾可能发生，也可能不发生一定不发生一定发生1.理解一个事件概率的意义.2.会在具体情境中求出一个事件的概率.学习目标活动1：抽纸团 在上节课的问题1中，从分别写有数字 1，2，3，4，5 的五个纸团中随机抽取一个，这个纸团里的数字有几种可能？每个数字被抽到的可能性大小是多少？12345有5种可能，即 1，2，3，4，5 .课堂导入可能性相同 活动2：掷骰子 在上节课的问题2中，掷一枚六个面上分别刻有 1到6 的点数的骰子，向上一面出现的点数有几种可能？每种点数出现的可能性大小是多少？有6种可能，即 1，2，3，4，5 ，6 .可能性相同 一般地，对于一个随机事件A，我们把刻画其发生可能性大小的数值，称为随机事件A发生的概率，记为P(A).概率的定义知识点新知探究活动3 掷一枚硬币，落地后: （1）会出现几种可能的结果？（2）正面朝上与反面朝上的可能性会相等吗？（3）试猜想：正面朝上的可能性有多大呢？开始正面朝上反面朝上两种相等 回忆刚才以上试验，它们有什么共同特点吗？可以发现，以上试验有两个共同特点：（1）每一次试验中，可能出现的结果只有有限个；（2）每一次试验中，各种结果出现的可能性相等.在这些试验中出现的事件为等可能事件. 一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m种结果，那么事件A发生的概率为：概率的计算 概率的取值范围：(1) 当A为必然事件时，P(A) =1；(2) 当A为随机事件时，0