2021北京海淀高一下学期期中数学试卷及答案

这是一份2021北京海淀高一下学期期中数学试卷及答案，共9页。试卷主要包含了04，已知向量，则l，在△ABC中，A为钝角，则点，对函数的图像分别作以下变换， “”是“”的，已知函数等内容，欢迎下载使用。

2021.04
学校___________姓名______________班级___________学号_______________
一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1.若角a的终边经过点，则
A.B. C. D.
2.已知向量，则l
A.3B.C. 5D.
3.
A.B. C. D.
4.在△ABC中，A为钝角，则点
A.在第一象限B、在第二象限C.在第三象限D.在第四象限
5.下列函数中，周期为π且在区间上单调递增的是
A.B. C. D.
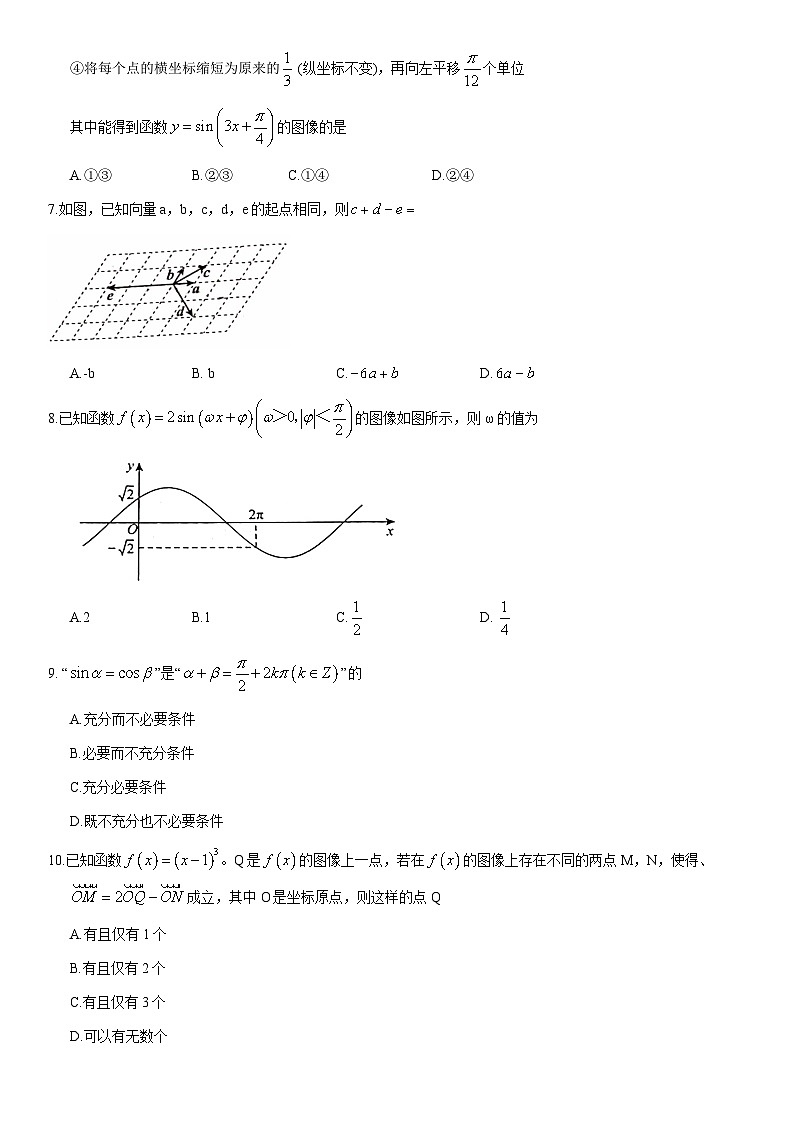
6.对函数的图像分别作以下变换：
①向左平移个单位，再将每个点的横坐标缩短为原来的 (纵坐标不变)；
②向左平移个单位，再将每个点的横坐标缩短为原来的 (纵坐标不变)
③将每个点的横坐标缩短为原来的 (纵坐标不变)，再向左平移个单位
④将每个点的横坐标缩短为原来的 (纵坐标不变)，再向左平移个单位
其中能得到函数的图像的是
A.①③B.②③C.①④D.②④
7.如图，已知向量a，b，c，d，e的起点相同，则
A.-bB. bC. D.
8.已知函数的图像如图所示，则ω的值为
A.2B.1C. D.
9. “”是“”的
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
10.已知函数。Q是的图像上一点，若在的图像上存在不同的两点M，N，使得、成立，其中O是坐标原点，则这样的点Q
A.有且仅有1个
B.有且仅有2个
C.有且仅有3个
D.可以有无数个
二、填空题：本大题共5小题，每小题4分，共20分，把答案填在题中横线上。
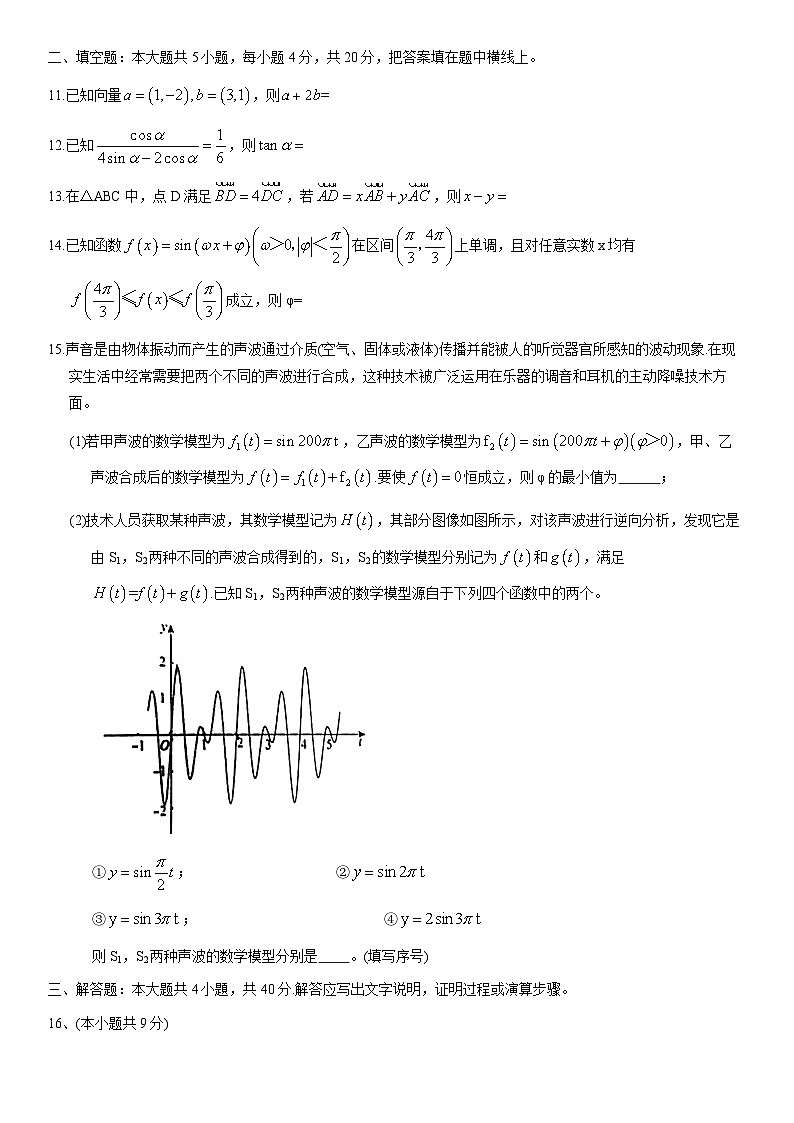
11.已知向量，则
12.已知，则
13.在△ABC中，点D满足，若，则
14.已知函数在区间上单调，且对任意实数x均有成立，则φ=
15.声音是由物体振动而产生的声波通过介质(空气、固体或液体)传播并能被人的听觉器官所感知的波动现象.在现实生活中经常需要把两个不同的声波进行合成，这种技术被广泛运用在乐器的调音和耳机的主动降噪技术方面。
(1)若甲声波的数学模型为，乙声波的数学模型为，甲、乙声波合成后的数学模型为.要使恒成立，则φ的最小值为 ；
(2)技术人员获取某种声波，其数学模型记为，其部分图像如图所示，对该声波进行逆向分析，发现它是由S1，S2两种不同的声波合成得到的，S1，S2的数学模型分别记为和，满足.已知S1，S2两种声波的数学模型源自于下列四个函数中的两个。
①；②
③；④
则S1，S2两种声波的数学模型分别是 。(填写序号)
三、解答题：本大题共4小題，共40分.解答应写出文字说明，证明过程或演算步骤。
16、(本小题共9分)
已知函数
(Ⅰ)求的定义域；
(Ⅱ)若，且，求的值。
17.(本小题共9分)
已知点，M是线段AB的中点。
(1)求点M和的坐标：
(Ⅱ)若D是x轴上一点，且满足，求点D的坐标。
18.(本小题共11分)
已知函数
（Ⅰ）某同学利用五点法画函数在区间上的图像.他列出表格，并填入了部分数据，请你帮他把表格填写完整，并在坐标系中画出图像；
（Ⅱ）已知函数。
(i)若函数的最小正周期为，求的单调递增区间；
(ii)若函数在上无零点，求ω的取值范围(直接写出结论)。
19.本小题共11分
若定义城R的函数满足：
①，②。则称函数满足性质。
(Ⅰ)判断函数与是否满足性质，若满足，求出T的值；
(Ⅱ)若函数满足性质判断是否存在实数a，使得对任意，都有，并说明理由；
(Ⅲ)若函数满足性质，且.对任意的，都有，求函数的值域。
2021北京海淀高一（下）期中数学
参考答案
一、选择题：
二、填空题：
11.(7,0)12. 2 13. 14. 15.；②③
注：第15题每空2分，其中第二空只有完整填写②③的才能得2分，其它答案均得0分.
三、解答题
16．（本小题9分）
解:（Ⅰ）依题意，.……………………………………………………………………….1分
所以有 .………………………………………………………………….3分
所以函数的定义域为. ………………………………………………….4分
（Ⅱ = 2 \* ROMAN ）. ……………………………………………………….5分
由，得.
又因为，
所以. ………………………………………………………7分
所以.………………………………………………………………………8分
所以.………………………………………………………………………9分
17.（本小题9分）
解：（Ⅰ）∵点，且M是线段AB的中点,
因为，
所以点M的坐标为. ………………………………………………………………………2分
.……………………………………………………….4分
（Ⅱ）设，则，. ……………………………………….6分
因为,
所以.………………………………………………………………….8分
解得.
所以点D的坐标为.………………………………………………………………….9分
18. （本小题11分）
解：（Ⅰ）
…………………………………………………………………………………………………3分

…………………………………………………………………………………………………6分
（Ⅱ）（ = 1 \* rman i）由题意，，
，，……………………………………………………………………………7分
即.
令,
解得.………………………………………………………………………8分
所以的单调递增区间为. ………………………………………9分
（ = 2 \* rman ii）的取值范围为. ………………..………………………………………………11分
19. （本小题11分）
解：（Ⅰ）函数满足性质.………………………………………………………1分
显然函数满足①，
对于②，由有，，所以，即. …………2分
函数显然不满足①，所以不满足性质. ………………………………………3分
（Ⅱ）存在.………………………………………………………………………………………4分
理由如下：
由，
可得.
即.
令，得.……………………………………………………………6分
（Ⅲ）依题意，对任意的有，所以. 因为函数满足性质,
由①可得, 在区间上有，又因为，所以. 可得
. 又因为对任意的有，所以.…………………7分
递推可得
函数,
因为所以
由②及可得，
所以当.
易知当时，，所以.
即时，.
所以当时，.……………………………8分
当时, （但时, ，需要排除）
显然, 此时随的增大而减小, 所以.
所以求值域时, 只需取, 得.
当时,
显然, 此时随的增大而减小, .
只需取, 得.
综上, 函数值域为………………………………11分
注：本试卷各题中若有其他合理的解法请酌情给分.
考生须知
1.本试卷共6页，共三道大题，19道小题，满分100分，考试时间90分钟。
2.在试卷上准确填写学校名称、班级、姓名。
3.试题答案一律填写在试卷上。
4.考试结束，请将本试卷交回。
X
0
π
2π
0
2
0
0
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
A
C
D
C
B
A
0
0
2
0
0