2023-2024学年山东省青岛市西海岸新区育才初级中学九年级（下）期初数学试卷（含解析）

这是一份2023-2024学年山东省青岛市西海岸新区育才初级中学九年级（下）期初数学试卷（含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

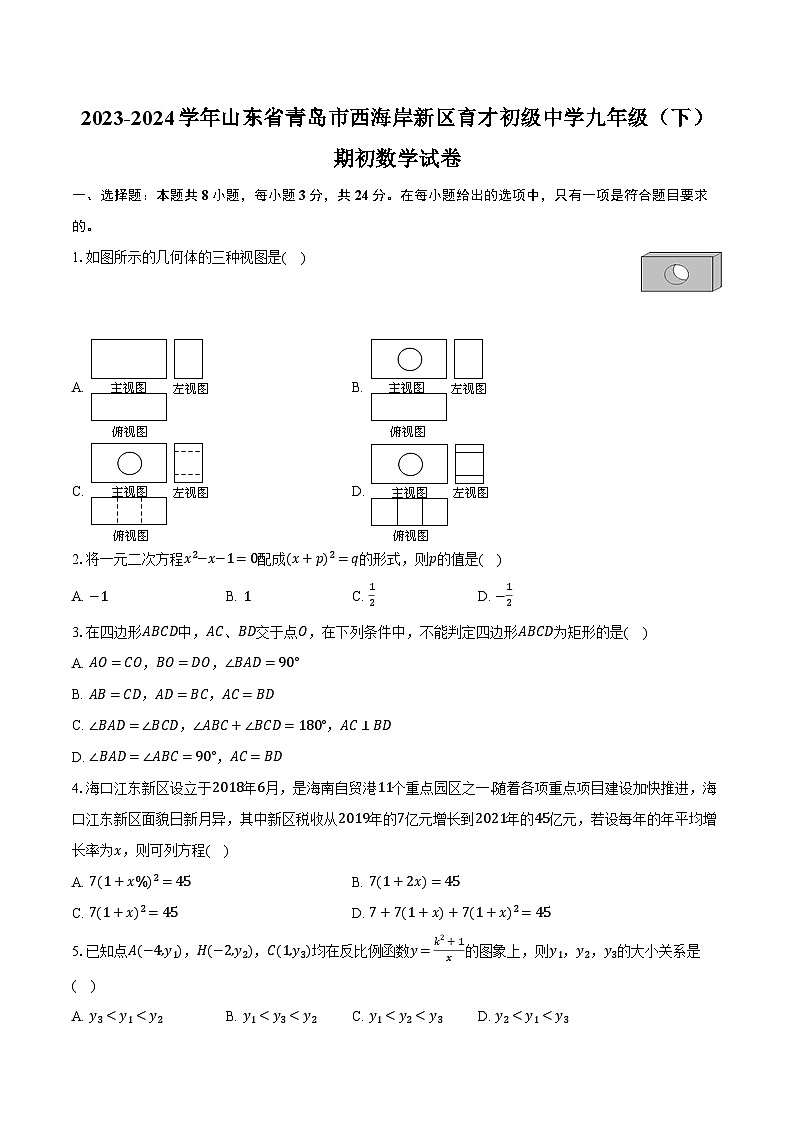
1.如图所示的几何体的三种视图是( )
A. B.
C. D.
2.将一元二次方程x2−x−1=0配成(x+p)2=q的形式，则p的值是( )
A. −1B. 1C. 12D. −12
3.在四边形ABCD中，AC、BD交于点O，在下列条件中，不能判定四边形ABCD为矩形的是( )
A. AO=CO，BO=DO，∠BAD=90°
B. AB=CD，AD=BC，AC=BD
C. ∠BAD=∠BCD，∠ABC+∠BCD=180°，AC⊥BD
D. ∠BAD=∠ABC=90°，AC=BD
4.海口江东新区设立于2018年6月，是海南自贸港11个重点园区之一.随着各项重点项目建设加快推进，海口江东新区面貌日新月异，其中新区税收从2019年的7亿元增长到2021年的45亿元，若设每年的年平均增长率为x，则可列方程( )
A. 7(1+x%)2=45B. 7(1+2x)=45
C. 7(1+x)2=45D. 7+7(1+x)+7(1+x)2=45
5.已知点A(−4,y1)，H(−2,y2)，C(1,y3)均在反比例函数y=k2+1x的图象上，则y1，y2，y3的大小关系是( )
A. y36.把抛物线y=−x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为( )
A. y=−(x−1)2+3B. y=−(x+1)2+3
C. y=−(x+1)2−3D. y=−(x−1)2−3
7.主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20米，一个主持人现站在舞台AB的黄金分割点点C处，则下列结论一定正确的是( )
①AB：AC=AC：BC；
②AC≈6.18米；
③AC=10( 5−1)米；
④BC=10(3− 5)米或10( 5−1)米．
A. ①②③④B. ①②③C. ①③D. ④
8.抛物线y=ax2+bx+c的对称轴是直线x=−1，且过点(1,0)，顶点位于第二象限，其部分图象如图所示，给出以下判断：①abc>0；②4a−2b+c>0；③8a+c>0；④b2−4ac>0；其中正确的个数有( )
A. 2个
B. 3个
C. 4个
D. 1个
二、填空题：本题共8小题，每小题3分，共24分。
9.如果ab=cd=79，那么2a−3c2b−3d=______．
10.一个袋子中只装有红、白两种颜色的球，这些球的形状、质地等完全相同，其中白色球有3个，红色球有n个.在看不到球的条件下，随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀.同学们进行了大量重复试验，发现摸出白球的频率稳定在0.2附近，则n的值约为______．
11.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度，如图所示，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，则旗杆AB的高度为______m.
12.如图所示，某市世纪广场有一块长方形绿地长18m，宽15m，在绿地中开辟三条道路后，剩余绿地的面积为224m2，则图中x的值为______．
13.如图，AB为⊙O的直径，点C、D、E在⊙O上，且AD=CD，∠E=70°，则∠ABC的度数为______．
14.如图，直线y=x+4与y轴交于点A，与反比例函数y=kx(k≠0)的图象交于点C，过点C作CB⊥x轴于点B，AO=4BO，则k的值为______．
15.如图，在菱形ABCD中，对角线AC，BD交于点O，点E为AB的中点，点F在OD上，DF=OF，连接EF交OA于点G，若OG=1，连接CE，S△BEC=12，则线段CE的长为______．
16.在平面直角坐标系中，对于点P(x,y)，我们把点P′(−y+1,x+1)叫作点P的伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，这样依次得到点A1，A2，A3，A4…，若点A1的坐标为(a,b)，对于任意的正整数n，点An均在x轴上方，则a，b应满足的条件为______．
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题4分)
请用圆规和直尺作图，不写作法，但要保留作图痕迹．
已知线段a，b，求作矩形ABCD，使对角线AC=a，边BC=b．
18.(本小题8分)
(1)解方程：2x2−4x+1=0
(2)计算：tan45°−cs60°sin60∘⋅tan30°．
19.(本小题6分)
中国古代的“四大名著”是指《红楼梦》《三国演义》《西游记》《水浒传》，“四大名著”是中国文学史中的经典作品，是世界宝贵的文化遗产.某校举行文化节讲名著活动，现将四大名著制作为卡片，《红楼梦》《三国演义》《西游记》《水浒传》分别对应的编号为A，B，C，D(除编号外，卡片其余完全相同)，将它们背面朝上，洗匀后放在桌面上．
(1)琳琳随机抽取1张卡片，抽到卡片编号为B的概率为______．
(2)若琳琳从这四张卡片中随机抽取一张，明明接着从余下的3张卡片中随机抽取1张，请用列表或画树状图的方法求琳琳、明明两人中恰好有一人抽中《红楼梦》(即A卡片)的概率．
20.(本小题7分)
图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°，长为3米的真空管AB与水平线AD的夹角∠BAD为37°，倾斜屋顶上的E处到水平线的距离DE为1.3米，C、D、E在同一直线上，且CD⊥AD.求安装热水器的铁架水平横管BC的长度(参考数据：sin37°≈35，cs37°≈45，tan37°≈34，sin22°≈38，cs22°≈93100，tan22°≈25，结果精确到0.1米)．
21.(本小题8分)
如图，已知A(−3,2)，B(n,−3)是一次函数y=kx+b的图象与反比例函数y=mx的图象的两个交点．
(1)求反比例函数的解析式；
(2)求△AOB的面积；
(3)在坐标轴上是否存在一点P，使△AOP是直角三角形？直接写出点P的坐标．
22.(本小题9分)
如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF/​/BC，AF与CE的延长线相交于点F，连接BF．
(1)求证：四边形AFBD是平行四边形；
(2)当△ABC满足什么条件时，四边形AFBD是菱形？请说明理由．
23.(本小题10分)
如图①是古代的一种远程投石机，其投出去的石块运动轨迹是抛物线的一部分．据《范蠡兵法》记载：“飞石重二十斤，为机发，行三百步”，其原理蕴含了物理中的“杠杆原理”．
在如图②所示的平面直角坐标系中，将投石机置于斜坡OA的底部(原点O处)，石块从投石机竖直方向上的点C处被投出，在斜坡上的点A处建有垂直于水平面的城墙AB.已知，石块运动轨迹所在抛物线的顶点坐标是(50,25)，OC=5，OD=75，AD=12，AB=9．
(1)求抛物线的表达式；
(2)通过计算说明石块能否飞越城墙AB；
(3)分别求出0≤x≤37.5和37.524.(本小题8分)
阅读材料
通过前面的学习我们已经知道了两点之间的距离，点到直线的距离和两条平行线间的距离，那么我们如何在平面直角坐标系中求这些距离呢？
如图，在平面直角坐标系xOy中，A、B两点的坐标分为A(x1,y1)，B(x2,y2)，由勾股定理得AB2=|x1−x2|2+|y1−y2|2，所以A、B两点间的距离为AB= |x1−x2|2+|y1−y2|2.这样就可以求出平面直角坐标系中任意两点间的距离．
我们用下面的公式可以求出平面直角坐标系中任意一点到某条直线的距离：
已知点P(x0,y0)和直线y=kx+b，则点P到直线y=kx+b的距离d可用公式d=|kx0−y0+b| 1+k2．
计算：例如：求点P(−2,1)到直线y=x+1的距离．
解：因为直线y=x+1可变形为x−y+1=0，其中k=1，b=1．
所以点P(−2,1)到直线y=x+1的距离了为d=|kx0−y0+b| 1+k2=|1×(−2)−1+1| 1+12=2 2= 2．
根据以上材料，解决下列问题：
(1)已知A(−2,1)，B(4,3)，写出线段AB的长度______；(只写答案)
(2)点P(1,1)到直线y=3x−2的距离，并说明点P与直线的位置关系；
(3)已知直线y=−2x+1与y=−2x+3平行，求这两条直线的距离．
25.(本小题12分)
如图，在▱ABCD中，AB=6cm，AD=AC=5cm，点P由C出发沿CA方向匀速运动，速度为1cm/s；同时，线段EF由AB出发沿AD方向匀速运动，速度为1cm/s，交AC于Q，连接PE、PF，若运动时间为t(s)(0(1)当t为何值时，PE/​/CD？
(2)求△PEQ的面积s与t的函数关系式；并确定当t为何值时，△PEQ的面积为△AQE面积的12？
(3)试探究五边形ABFPE的面积是否为定值？如果是定值，请求出它的面积；如果不是定值，请说明理由．
答案和解析
1.【答案】C
【解析】解：该图形的主视图为长方形，并且里边有一个小圆形，左视图为矩形，里边有两条横向虚线，俯视图为矩形，里面有两条纵向虚线．
故选C．
分别找到找到从正面、上面、左面看所得到的图形即可．
本题考查了三视图的知识，主视图是从物体的正面看得到的视图，左视图是从物体的左面看得到的视图，俯视图是从物体的上面看得到的视图．
2.【答案】D
【解析】解：x2−x−1=0，
移项，得x2−x=1，
配方，得x2−x+(12)2=1+(12)2，
(x−12)2=54，
即p=−12．
故选：D．
先移项，再配方得出x2−x+(12)2=1+(12)2，再求出答案即可．
本题考查了解一元二次方程，能正确配方得出x2−x+(12)2=1+(12)2是解此题的关键．
3.【答案】C
【解析】解：A、∵AO=CO，BO=DO，
∴四边形ABCD是平行四边形，
又∵∠BAD=90°，
∴平行四边形ABCD是矩形，故选项A不符合题意；
B、∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
又∵AC=BD，
∴平行四边形ABCD是矩形，故选项B不符合题意；
C、∵∠ABC+∠BCD=180°，
∴AB/​/CD，
∵∠BAD=∠BCD，
∴∠ABC+∠BAD=180°，
∴AD//BC，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形，故选项C符合题意；
D、∵∠BAD=∠ABC=90°，
∴AD//BC，
在Rt△ABD和Rt△BAC中，
AB=BABD=AC，
∴Rt△ABD≌Rt△BAC(HL)，
∴AD=BC，
∴四边形ABCD是平行四边形，
又∵AC=BD，
∴平行四边形ABCD是矩形，故选项D不符合题意；
故选：C．
由平行四边形的判定与性质、矩形的判定以及菱形的判定分别对各个选项进行判断即可．
本题考查了平行四边形的判定与性质、矩形的判定、菱形的判定以及全等三角形的判定与性质等知识，熟练掌握矩形的判定和菱形的判定是解题的关键．
4.【答案】C
【解析】解：由题意可得，
7(1+x)2=45，
故选：C．
根据题意和题目中的数据，可以得到方程7(1+x)2=45，然后即可判断哪个选项符合题意．
本题考查由实际问题抽象出一元二次方程，解答本题的关键是明确题意，列出相应的方程，这是一道典型的增长率问题．
5.【答案】D
【解析】解：在反比例函数y=k2+1x中，
∵k2+1>0，
∴反比例函数图象分布在第一、三象限，在每个象限内，y随x的增大而减小，
∵点C(1,y3)在第一象限，
∴y3>0，
∵A(−4,y1)，H(−2,y2)在第三象限，且−4<−2，
∴0>y1>y2，
∴y2故选：D．
根据反比例函数的性质进行解答即可．
本题考查了反比例函数图象上点的坐标特征，熟练掌握反比例函数的性质是解答本题的关键．
6.【答案】B
【解析】解：抛物线y=−x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为：y=−(x+1)2+3．
故选：B．
根据二次函数图象平移的方法即可得出结论．
本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的法则是解答此题的关键．
7.【答案】D
【解析】解：AB的黄金分割点为点C处，若AC>BC，则AB：AC=AC：BC，所以①不一定正确；
AC≈0.618AB≈12.36或AC≈20−12.36=7.64，所以②错误；
若AC为较长线段时，AC= 5−12AB=10( 5−1)，BC=10(3− 5)；若BC为较长线段时，BC= 5−12AB=10( 5−1)，AC=10(3− 5)，所以③不一定正确，④正确．
故选：D．
根据黄金分割的定义和AC为较长线段或较短线段进行判断．
本题考查了黄金分割：把线段AB分成两条线段AC和BC(AC>BC)，且使AC是AB和BC的比例中项(即AB：AC=AC：BC)，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AC= 5−12AB≈0.618AB，并且线段AB的黄金分割点有两个．
8.【答案】B
【解析】解：二次函数开口向下，则a<0，
二次函数对称轴为x=−1，
∴−b2a=−1，即b=2a<0．
由图象得交y轴的正半轴，
∴c>0．
∴abc>0．
故①正确．
由对称性可得二次函数与x轴的另一交点为(−3,0)，
∴由函数图象可得x=−2时，y>0．
∴4a−2b+c>0．
故②正确．
由函数图象可得x=2时，y<0，
∴4a+2b+c<0，b=2a代入得：8a+c<0，
故③错误．
抛物线与x轴有两个交点，
∴b2−4ac>0．
故④正确．
综上，正确的有：①②④．
故选：B．
依据题意，根据二次函数的性质可得a<0，b=2a>0，c>0，可判断结论①；由x=−2处的函数值可判断结论②；由x=2处函数值可判断结论③；由抛物线与x轴的交点可判断④．
本题考查了二次函数图象与系数的关系，掌握二次函数的图象与各项系数符号的关系是解题关键．
9.【答案】79
【解析】解：∵ab=cd=79，
∴2a2b=−3c−3d=79，
∴2a−3c2b−3d=79．
故答案为：79．
根据合比性质求解即可．
本题考查了比例的性质，主要利用了合比性质．
10.【答案】12
【解析】解：依题意得，33+n=0.2，
解得，n=12，
经检验，n=12是原分式方程的解，
故答案为：12．
依题意列出分式方程，计算求出满足要求的解即可．
本题考查了用频率估计概率，分式方程的应用，简单的概率计算．熟练掌握用频率估计概率，分式方程的应用，简单的概率计算是解题的关键．
11.【答案】13.5
【解析】解：设CD与EH交于G，
∵CD⊥FB，AB⊥FB，
∴CD/​/AB，
∴△CGE∽△AHE，
∴CGAH=EGEH，
即：CD−EFAH=FDFD+BD，
∴3−1.6AH=22+15，
∴AH=11.9，
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m)．
故答案为：13.5．
利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB=EF=1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出CGAH=EGEH，把相关条件代入即可求得AH=11.9，于是得到结论．
本题考查了相似三角形的应用，主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．
12.【答案】1m
【解析】解：根据题意得：(18−2x)(15−x)=224，
整理得：x2−24x+23=0，
解得：x1=1，x2=23(不符合题意，舍去)，
即图中x的值为1m，
故答案为：1m．
由题意：剩余绿地的面积为224m2，列出一元二次方程，解方程即可．
本题考查了一元二次方程的应用题，找准等量关系，正确列出一元二次方程是解题的关键．
13.【答案】40°
【解析】解：如图，连接AE、BD，
∵AB为⊙O的直径，
∴∠AEB=90°，
∵∠DEB=70°，
∴∠AED=∠AEB−∠DEB=20°，
∵AD=CD，
∴∠CBD=∠DBA=∠AED=20°，
∴∠ABC=∠ABD+∠CBD=20°+20°=40°，
故答案为：40°．
连接AE、BD，由圆周角定理得出∠AEB=90°，进而结合题意得出∠AED=20°，由圆心角、弧、弦的关系定理∠CBD=∠DBA=∠AED=20°，即可求出∠ABC的度数．
本题考查了圆周角定理，圆心角、弧、弦的关系，熟练掌握圆周角定理，圆心角、弧、弦的关系定理是解决问题的关键．
14.【答案】5
【解析】解：在直线y=x+4中，令x=0，则y=4，
∴A(0,4)即OA=4，
∵AO=4BO，
∴BO=1，
在直线y=x+4中，令x=1，则y=5
∴C(1,5)，
∵点C(1,5)在反比例函数y=kx的图象上，
∴k=5．
故答案为：5．
先求出A点坐标，再根据AO=4BO，得到点B的横坐标，将横坐标代入直线解析式可得点C坐标，k值可得．
本题考查了反比例函数与一次函数图象的交点问题，交点坐标满足两个函数关系式．
15.【答案】3 5
【解析】解：作EM⊥OA于M，
∵四边形ABCD是菱形，
∴BD⊥OA，OD=OB，OA=OC，
∴EM/​/OB，
∴AM：MO=AE：EB，
∵AE=BE，
∴AM=OM，
∴EM是△ABO的中位线，
∴EM=12OB，
∵DF=OF，
∴OF=12OD，
∴EM=OF，
∵∠MEG=∠OFG，∠MGE=∠OGF，
∴△EMG≌△FOG(AAS)，
∴MG=OG=1，
∴OM=2OG=2，
∴OA=2OM=4，
∴AC=2OA=8，
∵AE=BE，
∴△BAC的面积=2×△BEC的面积=2×12=24，
∴12AC⋅OB=24，
∴OB=6，
∴EM=12OB=3，
∵CM=OM+OC=2+4=6，
∴CE= CM2+EM2=3 5．
故答案为：3 5．
作EM⊥OA于M，由菱形的性质，平行线分线段成比例定理证明EM是ABO的中位线，得到EM=12OB，因此OF=EM，推出△EMG≌△FOG，得到MG=OG=1，从而求出OA的长，得到AC的长，求出CM的长，由三角形面积公式求出OB长，得到EM的长，由勾股定理即可求出CE的长．
本题考查菱形的性质，全等三角形的判定和性质，三角形中位线定理，关键是作EM⊥OA于M，证明△EMG≌△FOG，求出OA的长．
16.【答案】−1【解析】解：∵A1的坐标为(4,5)，
∴A2(−4,5)，A3(−4,−3)，A4(4,−3)，A5(4,5)，
…，
依此类推，每4个点为一个循环组依次循环，
∵点A1的坐标为(a,b)，
∴A2(−b+1,a+1)，A3(−a,−b+2)，A4(b−1,−a+1)，A5(a,b)，
…，
依此类推，每4个点为一个循环组依次循环，
∵对于任意的正整数n，点An均在x轴上方，
∴a+1>0−a+1>0，
−b+2>0b>0，
解得−1故答案为：−1根据“伴随点”的定义依次求出各点，不难发现，每4个点为一个循环组依次循环，用n除以4，根据商和余数的情况可确定点An的坐标；写出点A1(a,b)的“伴随点”，然后根据x轴上方的点的纵坐标大于0列出不等式组求解即可．
本题是对点的变化规律的考查，读懂题目信息，理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键，也是本题的难点．
17.【答案】解：①作射线BF，
②以点B为圆心，任意长为半径画弧交直线BF于M，N，
③分别以M，N为圆心，任意长为半径画弧，两弧交于一点E，
④作直线BE，
⑤在射线BF上截取BC=b，
⑥以C为圆心，a为半径画弧交于直线BE于一点A，
⑦分别以A，C为圆心，以BC，AB为半径画弧，两弧交于一点D，
⑧连接AD，CD，
矩形ABCD即为所求．
【解析】根据垂直平分线的作法及矩形的判定作图即可．
本题考查了作图复杂作图，矩形的判定，正确地找出图形是解题的关键．
18.【答案】解：(1)2x2−4x+1=0，
2x2−4x=−1，
x2−2x=−12，
x2−2x+1=−12+1，
(x−1)2=12，
x−1=± 12，
x1=2+ 22，x2=2− 22；
(2)原式=1−12 32× 33
=13．
【解析】(1)移项，系数化成1，配方，开方，即可得出两个一元一次方程，求出方程的解即可；
(2)把各个特殊角的三角函数值代入，再求出即可．
本题考查了解一元二次方程和特殊角的三角函数值的应用，主要考查学生对特殊角的三角函数值得记忆能力和知道如何选择适当的方法解一元二次方程，难度适中．
19.【答案】14
【解析】解：(1)琳琳随机抽取1张卡片，抽到卡片编号为B的概率=14；
故答案为：14；
(2)画树状图为：
共有12种等可能的结果，其中琳琳、明明两人中恰好有一人抽中《红楼梦》(即A卡片)的结果数为6种，
所以琳琳、明明两人中恰好有一人抽中《红楼梦》(即A卡片)的概率=612=12．
(1)直接利用概率公式计算；
本题考查了列表法与树状图法：利用列表法或树状图展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求出事件A或B的概率．
20.【答案】解：过B作BF⊥AD于F．
在Rt△ABF中，cs∠BAF=AFAB，
则AF=AB⋅cs∠BAF=3×cs37°≈2.4(米)，
∵BF⊥AD，CD⊥AD，BC//FD，
∴四边形BFDC是矩形．
∴BF=CD，BC=FD，
在Rt△EAD中，tan∠EAD=DEAD，
则AD=DEtan∠EAD≈1.325=3.25(米)，
∴BC=DF=AD−AF=3.25−2.4≈0.9(米)，
答：安装热水器的铁架水平横管BC的长度约为0.9米．
【解析】过B作BF⊥AD于F.根据余弦的定义求出AF，再根据正切的定义求出AD，计算即可．
本题考查的是解直角三角形的应用—坡度坡角问题，掌握坡角的概念、熟记锐角三角函数的定义是解题的关键．
21.【答案】解：(1)∵点A的坐标为(−3,2)在反比例函数y=mx的图象上，
∴m=xy=−3×2=−6，
∴反比例函数的解析式为y=−6x，
(2)∵点B的坐标为(n,−3)也在y=−6x上，
∴n=2，
∵A的坐标为(−3,2)，B的坐标为(2,−3)都在一次函数y=kx+b的图象上，代入得：
−3k+b=22k+b=−3，
解得k=−1b=−1，
∴一次函数的解析式为y=−x−1；
∵直线y=−x−1与x轴交于点C，如图1，

∴C(−1,0)，
∴OC=1，
∵A的坐标为(−3,2)，B的坐标为(2,−3)，
∴S△AOB=S△AOC+S△BOC=12OC⋅|yA|+12OC⋅|yB|=12OC(|yA|+|yB|)=12×1×(2+3)=52；
(3)当点P在x轴上，
设点P(m,0)，则OP=−m，
若∠OPA=90°时，如图2所示，

∵A的坐标为(−3,2)，
∴点P的坐标为(−3,0)；
当∠OAP=90°时，如图3，

∴OA2=32+22=13，AP2=(−3−m)2+(0−2)2，
∵△AOP是直角三角形，
∴OA2+AP2=OP2，即13+(m−3)2+(0−2)2=m2，
解得m=−133，
∴点P的坐标为(−133,0)；
当点P在y轴上时，
设点P(0,n)，则OP=n，
若∠OPA=90°时，如图4所示，

∵A的坐标为(−3,2)，
∴点P的坐标为(0,2)；
当∠OAP=90°时，如图5，

∴OA2=32+22=13，AP2=(n−2)2+(0+3)2，
∵△AOP是直角三角形，
∴OA2+AP2=OP2，即13+(n−2)2+(0+3)2=n2，
解得n=132，
∴点P的坐标为(0,132)；
综上可得点P的坐标为(−3,0)、(−133,0)、(0,2)或(0,132)．
【解析】(1)先把点A的坐标代入反比例函数y=mx求得m的值即可；
(2)把点B的坐标为(n,−3)代入反比例函数的解析式求得n，最后把A，B两点代入y=kx+b即可求得一次函数解析式，再利用一次函数的解析式求得点C的坐标，利用S△AOB=S△AOC+S△BOC即可求解；
(3)存在，在x轴和y轴上分两种情况：①若∠OAP=90°时，如图所示，利用两点间的距离公式和勾股定理即可求解；②若∠APO=90°时，如图所示，过点A作AP⊥x轴，垂足为点P，即可求解．
此题是反比例函数综合题，主要考查了待定系数法，三角形的面积公式，直角三角形的性质，用分类讨论和方程思想解决问题是解本题的关键．
22.【答案】(1)证明：∵E为AD的中点，D为BC中点，
∴AE=DE，BD=CD，
∵AF/​/BC，
∴∠AFE=∠DCE，∠FAE=∠CDE，
在△AFE和△DCE中，
∠AFE=∠DCE∠FAE=∠CDEAE=DE，
∴△AFE≌△DCE(AAS)，
∴AF=CD，
∴AF=BD，
∵AF/​/BD
∴四边形AFBD为平行四边形；
(2)解：当△ABC满足条件∠BAC=90°时，四边形AFBD是菱形，理由为：
∵E为AD的中点，D为BC中点，
∴AE=DE，BD=CD，
∵AF/​/BC，
∴∠AFE=∠DCE，∠FAE=∠CDE，
在△AFE和△DCE中，
∠AFE=∠DCE∠FAE=∠CDEAE=DE，
∴△AFE≌△DCE(AAS)，
∴AF=CD，
∴AF=BD，
∵AF/​/BD
∴四边形AFBD为平行四边形；
∵∠BAC=90°，D是BC的中点，
∴AD=12BC=BD，
∵四边形AFBD为平行四边形，AD=BD；
∴四边形AFBD为菱形．
【解析】(1)由AF/​/BC，得到两对内错角相等，再由E为中点，得到AE=DE，利用AAS得到△AFE与△CDE全等，利用全等三角形对应边相等得到AF=CD，再由BD=CD，等量代换得到AF=BD，利用一组对边平行且相等的四边形为平行四边形即可得证；
(2)由∠BAC=90°，AD为中线，利用斜边上的中线等于斜边的一半，得到AD=BD由邻边相等的平行四边为菱形，即可得证．
此题考查了平行四边形的判定，菱形的判定，全等三角形的判定与性质，以及等腰三角形与直角三角形的性质，熟练掌握判定与性质是解本题的关键．
23.【答案】解：(1)设石块的运动轨迹所在抛物线的解析式为y=a(x−50)2+25，
把(0,5)代入，得2500a+25=5，
解得a=−1125．
∴y=−1125(x−50)2+25=−1125x2+45x+5；
(2)石块不能飞越防御墙AB，理由如下：
把x=75代入y=−1125(x−50)2+25；
得y=20，
∵20<12+9，
∴石块不能飞越防御墙AB；
(3)设直线OA的解析式为y=kx，
把(75,12)代入得，k=425，
∴直线OA的解析式为y=425x，
过抛物线上的点M作MN⊥x轴交OA于N，
设M(m,−1125m2+45m+5)，则N(m,425m)，
∴MN=−1125m2+1625m+5，对称轴为x=−1625−2125=40，
∵a<0，在对称轴的左侧MN随x的增大而增大，
∴0≤x≤37.5时，a=37.5时，MN最大为714，
37.5答：0≤x≤37.5时，石块与斜坡OA在竖直方向上的最大距离为714；
37.5【解析】本题考查了二次函数在实际问题中的应用，理清题中的数量关系并熟练掌握二次函数的性质是解题的关键．
(1)设石块运行的函数关系式为y=a(x−50)2+25，用待定系数法求得a的值即可求得答案；
(2)把x=75代入y=−1125x2+45x+5，求得y的值，与21作比较即可；
(3)用待定系数法求得OA的解析式为y=425x，设出点M和N的坐标，再用含a的代数式表示出MN，最后根据二次函数的性质求解即可．
24.【答案】2 10
【解析】解：(1)∵A(−2,1)，B(4,3)，
∴AB= (−2−4)2+(1−3)2=2 10；
故答案为：2 10；
(2)∵直线y=3x−2变形得：3x−y−2=0，
∴点P(1,1)到直线y=3x−2的距离d=|3−1−2| 1+32=0，
则点P在直线上；
(3)找出直线y=−2x+1上一点(0,1)，
∵y=−2x+3，即2x+y−3=0，k=−2，b=3，
∴(0,1)到直线y=−x+3的距离d=|(−2)×0−1+3| 1+(−2)2=2 55，
则两平行线间的距离为2 55．
(1)由A与B的坐标，利用题中的方法求出AB的长即可；
(2)利用点到直线的距离公式求出P在直线的距离，即可作出判断；
(4)从直线y=−2x+1上找一个点(1,0)，求出该点到y=−2x+3的距离，即为两条平行线的距离．
本题考查了一次函数的点与直线之间的距离公式的运用，由函数的解析式求点的坐标的运用，平行线的性质的运用，解答时掌握点到直线的距离公式是关键．
25.【答案】解：(1)∵AE=BF=CP=t，
∴AP=5−t，
在▱ABCD中，AD=BC=AC=5，AB=EF=CD=6，
∵PE//CD，
∴△APE∽△ACD，
∴t5=5−t5，
解得：t=2.5，
∴当t=2.5时，PE/​/CD；
(2)如图1中，过点P作PH⊥EF于H，过点C作CG⊥AB于G．

∵CA=AC=BC，CG⊥AB，
∴AG=GB=3，CG= AC2−AG2= 52−32=4，
∵QE//AB//CD，
∴△AQE∽△ACD，
∴QECD=AEAD，即QE6=t5，QE=6t5，
∵AEAD=AQAC，AD=AC，
∴AE=AQ=t cm，
∵cs∠APH=cs∠ACG=45，
故PH=45PQ=45(5−2t)cm；
设△PEQ的面积为s，则s=12×65t⋅45(5−2t)=−2425t2+125t，
∵CP=t cm，AQ=t cm，
∴PQ=(5−2t)cm，
∵△PEQ的面积为△AQE面积的12，
∴PQ=2AQ，
∴5−2t=2t，
∴t=54，
故当t为54s时，△PEQ的面积为△AQE面积的12；
(3)在▱ABCD中，AD=BC=AC=5cm，AB=EF=CD=6cm，
∴∠CAB=∠CBA，
∵AB/​/EF，
∴∠CQF=∠CAB，∠CFQ=∠CBA，
∴∠CFQ=∠CQF，
∴CF=CQ，
∴AQ=BF=AE，
∴AP=CQ=CF，
∵AD/​/BC，
∴∠PAE=∠FCP，
∴△PAE≌△FCP(SAS)，
∴S△AEP=S△PCF，即S五边形BFPEA=S△ABC，
∴S五边形BFPEA=S△ABC=12×6×4=12(cm2).
答：五边形ABFPE的面积为12cm2．
【解析】(1)证明△APE∽△ACD，利用相似三角形的性质构建方程求解即可．
(2)过点P作PH⊥EF于H，过点C作CG⊥AB于G，根据相似三角形的判定和性质即可得到结论；
(3)由全等三角形知：△AEP、△EPC的面积相等，因此五边形的面积可转化为△ABC的面积，所以五边形的面积是个定值．
本题是四边形综合题目，考查了平行四边形的性质、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的判定与性质、平行线的性质、锐角三角函数定义、勾股定理以及三角形面积等知识；本题综合性强，熟练掌握平行四边形的性质和勾股定理，证明△PAE≌△FCP和△AQE∽△ACD是解题的关键，属于中考常考题型．