4 第八章 8.5空间直线、平面的平行关系 典型例题实战（练透核心考点）-2023-2024学年高一数学下学期期中期末高效复习（人教A版必修第二册）

这是一份4 第八章 8.5空间直线、平面的平行关系 典型例题实战（练透核心考点）-2023-2024学年高一数学下学期期中期末高效复习（人教A版必修第二册），文件包含4第八章85空间直线平面的平行关系典型例题实战练透核心考点原卷版docx、4第八章85空间直线平面的平行关系典型例题实战练透核心考点解析版docx等2份试卷配套教学资源，其中试卷共53页， 欢迎下载使用。

练透核心考点一：直线与平面平行
1．（2023·新疆乌鲁木齐·统考一模）如图，在四棱锥中，平面ABCD，，，且，，E是PD的中点，点F在PC上，且．
(1)证明：平面PAB；
【答案】(1)证明见解析(2)
【详解】（1）证明：在线段上取点，使得，
所以，在中，，且，
因为在四边形中，，，
所以，，
所以，四边形是平行四边形，
所以，
因为平面，平面，
所以平面.
2．（2022秋·江西赣州·高二统考期末）如图，在直三棱柱中，，，，M为的中点.
(1)证明：平面；
【答案】(1)证明见解析
【详解】（1）
连接交于点，连接，
则有为的中点，M为的中点，
所以，
且平面，平面，
所以平面.
3．（2022·上海闵行·上海市七宝中学校考模拟预测）如图，在四棱锥中，底面是矩形，垂直于平面，，，，点、分别在线段、上，其中是中点，，连接．
(1)当时，证明：直线平行于平面；
【答案】(1)证明见解析
【详解】（1）
取中点，联结、，
因为是的中位线，
故，且，
又，且，
故四边形为平行四边形，
所以，又不在平面内，在平面内，
所以平行于平面；
4．（2023·四川凉山·统考一模）如图，底面为等边三角形的直三棱柱中，，，为的中点．
(1)当时，求证：平面；
【答案】(1)证明见解析
(2)
【详解】（1）证明：，取中点，连接，，如图所示，
∵为的中点，∴且，
又当时，则为的中点，
又∵，且，
∴，且，
∴，且，
∴四边形为平行四边形，
∴，
又∵平面，平面，
∴平面．
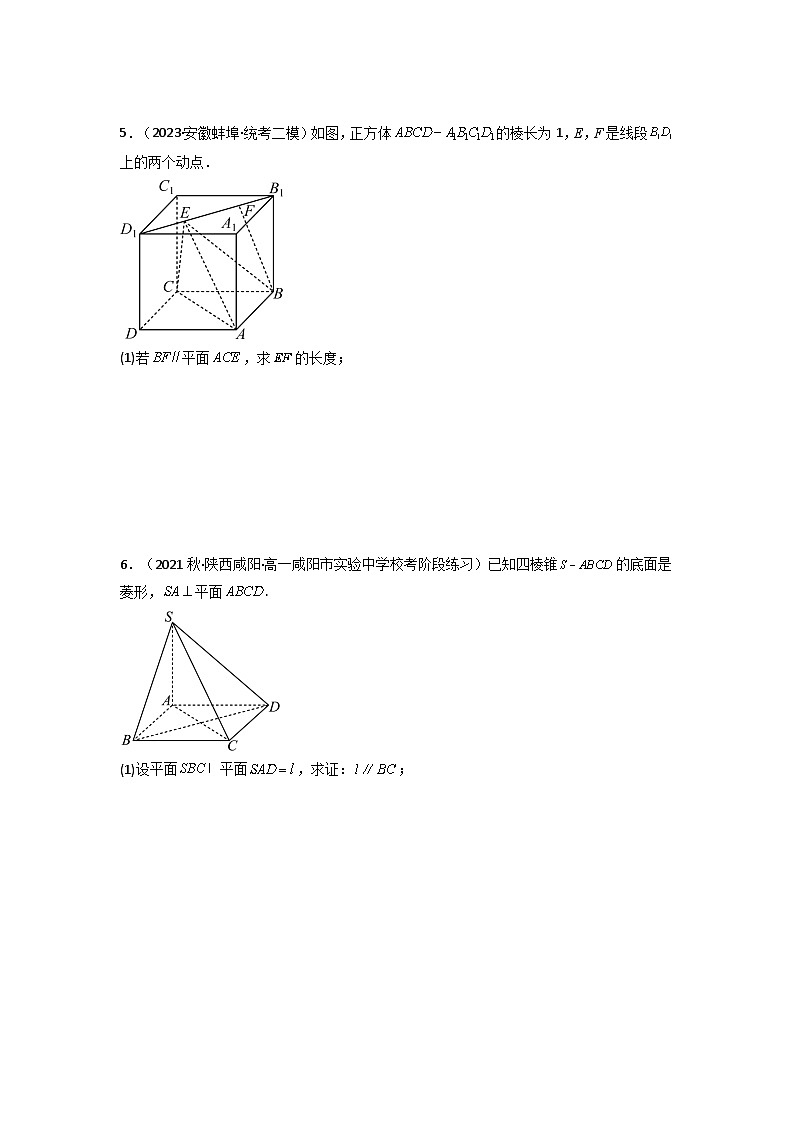
5．（2023·安徽蚌埠·统考二模）如图，正方体的棱长为1，E，F是线段上的两个动点．
(1)若平面，求的长度；
【答案】(1)
【详解】（1）正方体，连接交于点O，连接，如图所示，
∴平面，平面平面，平面，
∴，又，∴为平行四边形，
则.
6．（2021秋·陕西咸阳·高一咸阳市实验中学校考阶段练习）已知四棱锥的底面是菱形，平面.
(1)设平面平面，求证：；
【答案】(1)证明见解析
【详解】（1）平面平面，
平面，
又平面，平面平面，
.
7．（2023秋·内蒙古包头·高三统考期末）如图，直四棱柱的底面是平行四边形，，，，，，分别是，，的中点.
(1)证明：平面；
【答案】(1)证明见解析
【详解】（1）
连接，，
因为，分别是，的中点，所以，且，
又因为，且，所以四边形是平行四边形，
所以，且，
故，且，所以四边形是平行四边形，
所以，又平面，平面，
所以平面.
8．（2023秋·四川广元·高二统考期末）如图，四棱锥P－ABCD，平面PAB⊥平面ABCD，PA⊥AB，，∠DAB=90°，PA=AD，DC=2AB，E为PC中点.
(1)求证：直线//平面PAD；
【答案】(1)证明见解析
【详解】（1）证明：如图所示：
取PD中点，连接EF，AF，由为PC中点，
∴，又，
∴，故四边形ABEF为平行四边形.
∴，又平面，平面PAD，
∴//平面PAD.
9．（2023秋·浙江金华·高二统考期末）在四棱锥中，，PD与平面所成角的大小为，点Q为线段上一点．
(1)若平面，求的值；
【答案】(1)
【详解】（1）过点Q作交于E，连接．
，
四边形是平面四边形
又平面平面，平面PAD，平面，
，四边形是平行四边形，
，而,于是．
10．（2023·陕西宝鸡·校联考模拟预测）如图，在三棱柱中，平面平面ABC，四边形是边长为2的菱形，为等边三角形，，E为BC的中点，D为的中点，P为线段AC上的动点．
(1)若平面，请确定点在线段上的位置；
(2)若点为的中点，求三棱锥的体积．
【答案】(1)点P是线段AC上靠近点C的四等分点
(2)
【详解】（1）解：如图，连接与相交于，连接，连接交于点，
∵平面，平面平面，平面，
∴，
∵，，
∴，，又，所以，
∵，，
∴，
∴点是线段上靠近点的四等分点；
练透核心考点二：平面与平面平行
1．（2022秋·新疆巴音郭楞·高二校考期中）已知正方体ABCD-A1B1C1D1的棱长为a，点E、F分别是D1C和A1C1上的点，，则EF与平面AA1D1D的位置关系是（ ）
A．相交B．平行C．垂直D．不确定
【答案】B
【详解】，由于，
所以是的三等分点，
设是棱上靠近的三等分点，
则，
由于平面，平面，所以平面，
同理可证得平面，
由于平面，
所以平面平面，
由于平面，
所以平面.
故选：B
2．（2023·高一课时练习）下面四个正方体中，点A、B为正方体的两个顶点，点M、N、P分别为其所在棱的中点，能得出平面的图形序号是______．（写出所有符合条件的序号）
【答案】①②
【详解】
对于①，如图1.
因为点M、N、P分别为其所在棱的中点，所以，.
又，所以.
因为平面，平面，所以平面.
同理可得平面.
因为平面，平面，，
所以平面平面.
又平面，所以平面，故①正确；
对于②，如图2，连结.
因为点M、P分别为其所在棱的中点，所以.
又，且，所以，四边形是平行四边形，所以，
所以.
因为平面，平面，所以平面，故②正确；
对于③，如图3，连结、、.
因为点M、N、P分别为其所在棱的中点，所以，.
因为平面，平面，所以平面.
同理可得平面.
因为平面，平面，，
所以平面平面.
显然平面，平面，所以平面，且与平面不平行，所以与平面不平行，故③错误；
对于④：如图4，连接，因为为所在棱的中点，则，
故平面即为平面，由正方体可得，
而平面平面，
若平面，
由平面可得，
故，显然不正确，故④错误.
故答案为：①②.
3．（2023秋·河北唐山·高二统考期末）如图，在直三棱柱中，M，N分别为AC，的中点.
(1)证明：平面；
【答案】(1)证明见解析
【详解】（1）证明：取的中点H，连接MH，HN.
因为M为AC的中点，所以.
因为平面，平面，所以平面.
因为H，N分别为，的中点，所以，
因为平面，平面，所以平面.
因为面MHN，所以平面平面.
因为平面MHN，所以平面.
4．（2023·高一课时练习）平行四边形和平行四边形不在同一平面内，、分别为对角线，上的点，且．求证：平面．
【答案】证明见详解
【详解】在上取点，使得，则，
∵平面，平面，
∴平面，
连接，
∵，即，则，
∴，
又∵，则，且平面，平面，
∴平面，
，平面，
故平面平面，
由平面，可得平面.
5．（2022秋·江西上饶·高二江西省余干中学阶段练习）如图，直三棱柱ABC-A1B1C1中，M为BC的中点，，，．
(1)证明：A1B∥平面AMC1；
【答案】(1)证明见解析
【详解】（1）取的中点G，连接，和GM，由直三棱柱ABC-A1B1C1，和都是中点，
可得四边形和是平行四边形，，，又
，，平面平面，而平面，
A1B∥平面AMC1
6．（2022春·河南·高一校联考期中）如图，在正方体中，分别为所在棱的中点，分别为正方形和正方形的中心，连接，.
(1)证明：平面平面；
【答案】(1)证明见解析
【详解】（1）连接 ，则有 ，同理 ，
平面GEF，平面GEF，所以平面GEF，
平面GEF，平面GEF，所以平面GEF，
且 平面 ， 平面， ，
平面 平面；
7．（2022春·湖南衡阳·高二衡阳市一中校考阶段练习）如图，在三棱柱中，侧棱底面，，，，是中点，是中点，是与的交点，点在线段上.
(1)求证：平面；
【答案】(1)证明见解析
【详解】（1）连.连，连，
∵，，∴.
又面，面.∴面.
∵四边形是平行四边形，∴，
面，面，∴面，
∵，面，
∴面，面，∴面.
8．（2023秋·江西萍乡·高三统考期末）如图在五面体中，为等边三角形，平面平面，且，，为边的中点.
(1)证明：平面；
【答案】(1)证明见解析
【详解】（1）证明：取线段的中点，连接、，
、分别为、的中点，则，
平面，平面，平面，
在侧面中，，则，即，
又因为，所以，四边形为平行四边形，，
平面，平面，平面，
，、平面，所以，平面平面，
平面，平面.
9．（2022秋·陕西渭南·高一统考期末）在如图所示的多面体中，四边形是平行四边形，四边形是矩形，平面.
(1)求证：平面；
【答案】(1)证明见解析
(2)
【详解】（1）∵四边形是平行四边形，∴，
∵四边形是矩形，∴，
平面，平面，∴平面，同理平面，
∵平面，平面，，
∴平面平面，
∵平面，∴平面
10．（2022·四川雅安·统考一模）如图，在三棱柱中，侧面为正方形，平面ABC，，，E，F分别为棱AB和的中点.
(1)在棱上是否存在一点D，使得平面EFC？若存在，确定点D的位置，并给出证明；若不存在，试说明理由；
【答案】(1)答案见解析；
【详解】（1）存在点D，使得平面EFC.
取的中点D，的中点M，连接,则.
因为E，F分别为棱AB和的中点，
所以,所以.
连接,则.
因为平面，平面，
所以平面平面.
因为平面,所以平面.
所以存在D(D为中点)，使得平面EFC.
练透核心考点三：平行的综合问题
1．（2022秋·江西新余·高二新余市第一中学校考开学考试）如图，在棱长为的正方体中，、分别是棱、的中点，是侧面上一点，若平面，则线段长度的取值范围是（ ）
A．B．C．D．
【答案】B
【详解】如图所示，分别取棱、的中点、，连接、、、、，
因为、分别为、的中点，则，同理可得，，
平面，平面，平面，
因为且，、分别为、的中点，则且，
所以，四边形为平行四边形，所以，且，
且，且，
所以，四边形为平行四边形，，
平面，平面，平面，
，、平面，所以，平面平面，
当时，平面，则平面，
所以，点的轨迹为线段．
在中，．
在中，．
同理，在中，可得，所以，为等腰三角形．
设的中点为，连接．
当点位于的中点处时，，此时最短；当点位于、处时，最长．
易求得，
因此，线段长度的取值范围是．
故选：B.
2．（多选）（2023·全国·模拟预测）已知长方体中，点P，Q，M，N分别是棱AB，BC，，的中点，则下列结论不正确的是（ ）
A．平面B．平面
C．平面D．平面
【答案】ABC
【详解】A选项：如图1，若平面，则，
又因为平面，平面，
则，连接，又，
所以平面，平面，则，
只有当时，才成立，故A不正确；
B选项：如图2，连接AC，因为点P，Q分别是棱AB，BC的中点，
所以，平面，平面，
所以平面，
若平面，则平面平面，
又平面平面，平面平面，
所以，显然不正确，故B不正确；
C选项：如图3，若平面，平面，
则，又易知平面，平面，
则，又，
所以平面，平面则，
显然不正确，故C不正确；
D选项：如图4，连接AC，CN，因为点P，Q分别是棱AB，BC的中点，
所以，平面，平面，
所以平面，
因为Q，N分别是BC，的中点，所以，
所以四边形是平行四边形，则，
平面，平面，
所以平面，且，
因此平面平面，平面，
所以平面，故D正确．
故选:ABC.
3．（2021·江西·高三校联考阶段练习）如图，四棱柱中，四边形为平行四边形，点分别在线段上，且，点在上且平面平面，则________
【答案】##
【详解】平面平面，且平面平面，平面平面，所以，所以，
易得平面平面，又平面，所以平面，
因为平面平面，平面，所以平面，
又因为平面平面，
下面证明:如果一条直线与两个相交平面平行,则此直线平行两个平面的交线
如图所示，若平面，，则
过直线作平面，使得，，
因为，，则，同理，
所以，又，所以，
又，，所以，即得.
由上面证明可知，，故可确定一个平面，
又平面平面，平面平面，平面平面，所以，又，所以，所以.
故答案为：.
4．（2023春·广东·高二统考阶段练习）如图，在四面体OABC中，，，，用向量表示，则________．若，且 平面ABC，则实数________．
【答案】 ##0.75
【详解】
由条件可知：

；
延长 与AM交于D，连接BD，则当 时， 平面ABC，
平面ABC， 平面ABC；
令 ，则有 ，
，
根据向量基底表示法的唯一性，有： ，解得 ，
，
.
故答案为：，
5．（2023秋·江西吉安·高二统考期末）如图，在等腰直角中，，DB和EC都垂直于平面ABC，且，F为线段AE上一点，设.
(1)当时，求证：平面ABC；
【答案】(1)证明见解析
【详解】（1）取靠近点的三等分点为，连接,
则有,
又因为DB和EC都垂直于平面ABC，，
所以，所以,所以四边形为平行四边形，
所以,平面ABC，平面ABC,
所以平面ABC.
6．（2023春·湖北荆州·高二统考阶段练习）如图，在正方体中，E，F分别为，的中点．
(1)求证：平面；
【答案】(1)证明见解析
【详解】（1）作的中点G，连接EG，AG，如下图所示，
∵分别为的中点，则，，
且，，则，，
∴四边形ADEG是平行四边形，则，
∵分别为的中点，则，，
∴四边形是平行四边形，则，
故，且平面，平面，
∴平面．
7．（2023·四川凉山·统考一模）如图，在直三棱柱中，，，，，为的中点．
(1)当时，求证：平面；
【答案】(1)证明见解析
【详解】（1）取中点，连接，，为的中点，如图所示：
因为分别为和的中点，
所以且，
又当时，为的中点，
所以，且，
所以，且，
所以四边形为平行四边形，所以，
因为平面，平面，所以平面．
8．（2023·湖北武汉·统考模拟预测）如图，四棱台的下底面和上底面分别是边和的正方形，侧棱上点满足.
(1)证明：直线平面；
【答案】(1)证明见解析
【详解】（1）证明：延长和交于点，连接交于点，连接，
由，故，所以，所以，
所以，所以为中点，
又且，且，
所以且，
故四边形为平行四边形，
所以，又平面，平面，
所以平面.
9．（2023·云南·高三云南师大附中校考阶段练习）如图所示，在四棱柱中，以A为端点的三条棱的长都为1，且两两夹角为，点M，N分别在线段和上，且满足，其中．
(1)判断直线与平面的位置关系，并证明你的结论；
【答案】(1)答案见解析
【详解】（1）延长交直线于点P，连接，如图．
由，可知．
，故，故，．
当时，平面平面，
平面．
当时，即为，故平面．
综上所述：当时，平面；当时，平面．
10．（2023秋·山东日照·高三校联考期末）如图，四棱锥的底面为正方形，平面，，是侧面上一点．
(1)过点作一个截面，使得与都与平行．作出与四棱锥表面的交线，并证明；
【答案】(1)答案和证明见解析
【详解】（1）过点作的平行线，分别交于点，
过作的平行线，交于点，过作的平行线交于点，
则截面为所求截面，证明如下：
因为截面,截面,所以截面,
因为截面,截面,所以截面.
11．（2023春·江苏南京·高三南京市第一中学校考开学考试）如图，在等腰直角三角形ABC中，，D是AC的中点，E是AB上一点，且．将沿着DE折起，形成四棱锥，其中A点对应的点为P．
(1)在线段PB上是否存在一点F，使得平面PDE？若存在，指出的值，并证明；若不存在，说明理由；
【答案】(1)存在，
【详解】（1）当时，平面PDE，证明如下：
过点C作，垂足为H，
在PE上取一点M，使得，连接HM，FM，
因为，，所以且，
因为D是AC的中点，且，所以且，
所以且，所以四边形CFMH是平行四边形，即，
又因为平面PDE，平面PDE，所以平面PDE；
12．（2022秋·上海黄浦·高二校考期末）如图，正四棱锥的底面边长为a，侧棱长为2a，点P、Q分别在BD和SC上，并且，平面，求线段PQ的长．
【答案】
【详解】如图，过作，交于，连结，
因为，，
所以，又平面，平面，
所以平面，又平面，
又，平面，
所以平面平面，又平面平面，平面平面，
，
由，可得，
，
，，
，
，
所以，
所以线段的长为．
13．（2022·全国·高三专题练习）如图、三棱柱的侧棱垂直于底面，是边长为2的正三角形，，点在线段上且，点是线段上的动点．当为多少时，直线平面？
【答案】.
【详解】当点是线段上靠近点的三等分点，即时，平面.
过点作交于点，过点作交于点，连接，
平面，平面，
平面，
，面，平面，
平面，
又，平面，平面，
∴平面平面，
平面，
平面．
∴，
当时，平面．