

人教版九年级数学上册同步精品讲义 第20课 垂径定理(原卷版+解析)
展开知识精讲
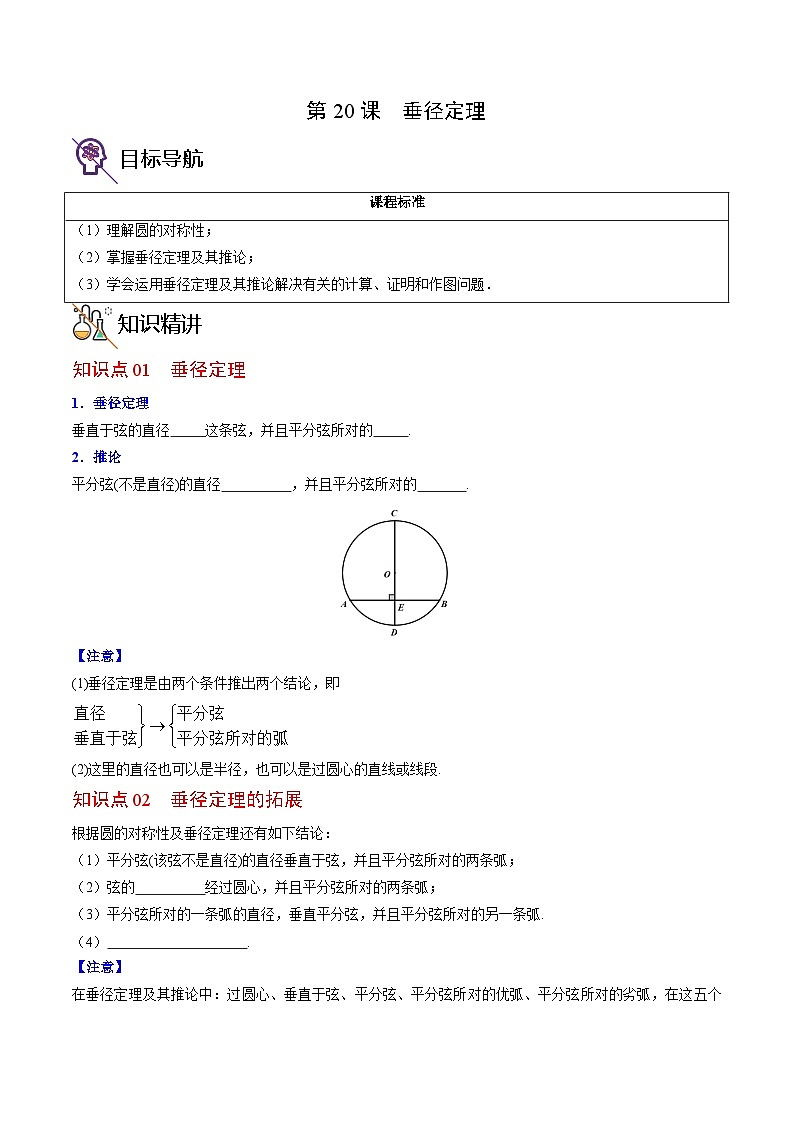
知识点01 垂径定理
1.垂径定理
垂直于弦的直径 这条弦,并且平分弦所对的 .
2.推论
平分弦(不是直径)的直径 ,并且平分弦所对的 .
【注意】
(1)垂径定理是由两个条件推出两个结论,即
(2)这里的直径也可以是半径,也可以是过圆心的直线或线段.
知识点02 垂径定理的拓展
根据圆的对称性及垂径定理还有如下结论:
平分弦(该弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
弦的 经过圆心,并且平分弦所对的两条弧;
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
.
【注意】
在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)
能力拓展
考法01 应用垂径定理进行计算与证明
【典例1】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为,水面宽为,则水的最大深度为( )
A.B.C.D.
【即学即练】筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米B.2米C.3米D.(4+)米
【典例2】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
【即学即练】如图,AB为⊙O的弦,OC⊥AB于点M,交⊙O于点C.若⊙O的半径为10,OM:MC=3:2,求AB的长.
考法02 垂径定理的综合应用
【典例3】如图,小丽荡秋千,秋千链子的长为,秋千向两边摆动的角度相同,摆动的水平距离为3米,秋千摆至最高位置时与最低位置时的高度之差(即)为0.5米.则秋千链子的长为( )
A.2米B.2.5米C.1.5米D.米
【即学即练】工程上常用钢珠来测量零件上小孔的宽口,如果钢珠的直径为10mm,钢珠上项端离零件上表面的距离为8mm,如图,则这个零件小孔的宽口AB等于( )mm.
A.4B.6C.7D.8
【典例4】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求所在圆的半径r的长;
(2)当洪水上升到跨度只有30米时,要采取紧急措施.若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?并说明理由.
【即学即练】如图,射线PG平分∠EPF,O为射线PG上的一点,以O为圆心,13为半径作⊙O,分别与∠EPF两边相交于点A,B和点C,D,连结OA,此时有OA∥PE.
(1)求证:AP = AO;
(2)若弦AB = 24,求OP的长.
分层提分
题组A 基础过关练
1.如图,⊙O的半径为4,弦心距OC=2,则弦AB的长为( )
A.3B.C.6D.
2.如图,为的直径,为的弦,为优弧的中点,,垂足为,,,则的半径为( )
A.B.C.D.
3.小明想知道一块扇形铁片中的的拱高(弧的中点到弦的距离)是多少?但他没有任何测量工具,聪明的小明观察发现身旁的墙壁是由的正方形瓷砖密铺而成(接缝忽略不计).他将扇形按如图方式摆放,点恰好与正方形瓷砖的顶点重合,根据以上操作,的拱高约是( )
A.B.C.D.
4.如图,CD是⊙O的直径,弦AB⊥CD于点E,则下列结论不一定成立的是( )
A.AE=BEB.OE=DEC.D.
5.下列语句中不正确的有( )
①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.
A.5个B.4个C.3个D.2个
6.如图是一个圆柱形输水管横截面的示意图,阴影部分为有水部分,如果水面AB的宽为8cm,水面最深的地方高度为2cm,则该输水管的半径为( )
A.3cmB.5cmC.6cmD.8cm
7.如图,在⊙O中,弦AB⊥OC于E点,C在圆上,AB=8,CE=2,则⊙O的半径AO=___________.
8.如图,⊙O的直径AB的长是20,弦CD⊥AB,垂足为点E, CD=16,则CE=____,BE=_____.
9.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
10.如图所示,已知为⊙的直径,是弦,且于点,连接AC、OC、BC.
(1)求证:;
(2)若,,求⊙的直径.
题组B 能力提升练
1.一个圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD的长为( )
A.2mB.4mC.6mD.8m
2.如图,的半径为,,经过点的的最短弦的长为( )
A.4B.6C.8D.10
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A.B.C.D.8
4.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是()
A.∠COE=∠DOEB.CE=DE
C.OE=BED.
5.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸B.24寸C.26寸D.28寸
6.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口的长度为( )
A.8mmB.6mmC.10mmD.0.9mm
7.如图,M是⊙O内一点,已知过点M的⊙O最长的弦为20cm,最短的弦长为16cm,则OM=_______cm.
8.如图,点O是半圆的圆心,D是以AB为直径的半圆上的一点,以OD为对角线作正方形OCDE,经过C,E的直线分别与半圆弧交于F,G.已知CE=6,则FG的长为______.
9.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
10.如图,AB是圆O的直径,点C、D为圆O上的点,满足:,AD交OC于点E.已知OE=3,EC=2
(1)求弦AD的长;
(2)请过点C作AB的平行线交弦AD于点F,求线段EF的长.
题组C 培优拔尖练
1.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块B.第二块C.第三块D.第四块
2.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2B.C.D.
3.如图,矩形ABCD是由边长为1的五个小正方形拼成,O是第2个小正方形的中心,将矩形ABCD绕O点逆时针旋转90°得矩形,现用一个最小的圆覆盖这个图形,则这个圆的半径是( )
A.B.C.D.
4.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A.B.4C.D.5
5.如图,AC是的直径,弦于E,连接BC,过点O作于F,若,,则OE的长为( )
A.3B.4C.D.5
6.如图,等腰梯形ABCD内接于半圆D,且AB=1,BC=2,则OA=( )
A.B.C.D.
7.如图,在⊙O内有折线ABCO,点A、B在圆上,点C在⊙O内,其中AB=9,OC=3,∠B=∠C=60°,则BC的长为_____.
8.如图, 在⊙O中,AB是⊙O的直径,,AB=8,M是AB上的一动点,CM+DM的最小值是_____________.
9.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D.
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
10.已知AB是半圆O的直径,OD⊥弦AC于D,过点O作交半圆O于点E,过点E作EF⊥AB于F.若AC=2,
(1)求OF的长;
(2)连接BE,若BE=,求半径OA的长.
课程标准
(1)理解圆的对称性;
(2)掌握垂径定理及其推论;
(3)学会运用垂径定理及其推论解决有关的计算、证明和作图问题.
第20课 垂径定理
目标导航
知识精讲
知识点01 垂径定理
1.垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
2.推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
【注意】
(1)垂径定理是由两个条件推出两个结论,即
(2)这里的直径也可以是半径,也可以是过圆心的直线或线段.
知识点02 垂径定理的拓展
根据圆的对称性及垂径定理还有如下结论:
平分弦(该弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
圆的两条平行弦所夹的弧相等.
【注意】
在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)
能力拓展
考法01 应用垂径定理进行计算与证明
【典例1】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为,水面宽为,则水的最大深度为( )
A.B.C.D.
【答案】C
【详解】解:如图所示:
输水管的半径为,水面宽为,水的最大深度为,
,
,,
,
∴
水的最大深度为:.
故选:C.
【即学即练】筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米B.2米C.3米D.(4+)米
【答案】A
【详解】解:根据题意和圆的性质知点C为的中点,
连接OC交AB于D,则OC⊥AB,AD=BD=AB=3,
在Rt△OAD中,OA=4,AD=3,
∴OD===,
∴CD=OC﹣OD=4﹣,
即点到弦所在直线的距离是(4﹣)米,
故选:A.
【典例2】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
【答案】(1)见解析
(2)
【详解】(1)证明:过O作OH⊥CD于H,如图1所示:
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH﹣CH=BH﹣DH,
∴AC=BD;
(2)解:过O作OH⊥CD于H,连接OD,如图2所示:
则CH=DH=CD,
∵OC=OD,∠OCD=60°,
∴△OCD是等边三角形,
∴CD=OC=4,
∴CH=2,
∴OH===2,
∴AH===2,
∴AC=AH﹣CH=2﹣2.
【即学即练】如图,AB为⊙O的弦,OC⊥AB于点M,交⊙O于点C.若⊙O的半径为10,OM:MC=3:2,求AB的长.
【答案】
【详解】解:如图,连接OA.
∵OM:MC=3:2,OC=10,
∴OM==6.
∵OC⊥AB,
∴∠OMA=90°,AB=2AM.
在Rt△AOM中,AO=10,OM=6,
∴AM=8.
∴AB=2AM =16.
考法02 垂径定理的综合应用
【典例3】如图,小丽荡秋千,秋千链子的长为,秋千向两边摆动的角度相同,摆动的水平距离为3米,秋千摆至最高位置时与最低位置时的高度之差(即)为0.5米.则秋千链子的长为( )
A.2米B.2.5米C.1.5米D.米
【答案】B
【详解】解:∵点D为的中点,
∴由垂径定理知OD⊥AB,AD=BD=AB=×3=1.5(米),
∴OA2=AD2+OD2,
则OA2=AD2+(OA-CD)2=1.52+(OA-0.5)2,
解得:OA=2.5(米).
故选:B.
【即学即练】工程上常用钢珠来测量零件上小孔的宽口,如果钢珠的直径为10mm,钢珠上项端离零件上表面的距离为8mm,如图,则这个零件小孔的宽口AB等于( )mm.
A.4B.6C.7D.8
【答案】D
【详解】连接OA,过点O作OD⊥AB于点D,
则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm.
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm.
在Rt△AOD中,∵mm,
∴AB=2AD=2×4=8mm
故选D
【典例4】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求所在圆的半径r的长;
(2)当洪水上升到跨度只有30米时,要采取紧急措施.若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?并说明理由.
【答案】(1)34
(2)不需要采取紧急措施,见解析
【详解】(1)解:连结OA,
由题意得:AD=AB=30,OD=(r−18),
在Rt△ADO中,由勾股定理得:
,
解得,r=34.
(2)解:连结,
∵OE=OP−PE=30,
∴在Rt△A′EO中,
由勾股定理得:,
∴,
解得:=16.
∴=32.
∵=32>30,
∴不需要采取紧急措施.
【即学即练】如图,射线PG平分∠EPF,O为射线PG上的一点,以O为圆心,13为半径作⊙O,分别与∠EPF两边相交于点A,B和点C,D,连结OA,此时有OA∥PE.
(1)求证:AP = AO;
(2)若弦AB = 24,求OP的长.
【答案】(1)见解析(2)
【详解】(1)证明:∵PG平分∠EPF
∴∠EPO=∠APO
∵OA∥PE
∴∠EPO=∠AOP
∴∠APO=∠AOP
∴AP=AO
(2)过点O作OH⊥AB于点H,如图,
根据垂径定理得到AH=BH==12
∴PH=PA+AH=AO+AH=13+12=25
在中,
由勾股定理得:
则OP的长为
故答案为:
分层提分
题组A 基础过关练
1.如图,⊙O的半径为4,弦心距OC=2,则弦AB的长为( )
A.3B.C.6D.
【答案】D
【详解】如图所示,连接
由题意知,弦心距OC=2,
则根据垂径定理,有
在中,
则
根据垂径定理可知,
故选D.
2.如图,为的直径,为的弦,为优弧的中点,,垂足为,,,则的半径为( )
A.B.C.D.
【答案】B
【详解】解:如图,连接,延长交于点T,设的半径为,
,
,
,
在和中,
,
,
,
在中,,
,
,
故选:B.
3.小明想知道一块扇形铁片中的的拱高(弧的中点到弦的距离)是多少?但他没有任何测量工具,聪明的小明观察发现身旁的墙壁是由的正方形瓷砖密铺而成(接缝忽略不计).他将扇形按如图方式摆放,点恰好与正方形瓷砖的顶点重合,根据以上操作,的拱高约是( )
A.B.C.D.
【答案】D
【详解】解:如图所示,通过数瓷砖的个数,可以得到OC=30cm,AB=40cm,
∵D为中点,
∴由垂径定理得OC垂直且平分AB,
∴BC=20cm,
∴cm,
∵OD=OB=cm,
∴CD=OD-OC=cm,
即拱高为cm,
故选D.
4.如图,CD是⊙O的直径,弦AB⊥CD于点E,则下列结论不一定成立的是( )
A.AE=BEB.OE=DEC.D.
【答案】B
【详解】解:是的直径,弦于点,
,, .
故选:B.
5.下列语句中不正确的有( )
①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.
A.5个B.4个C.3个D.2个
【答案】B
【详解】因为能够完全重合的弧是等弧,故①不正确;
垂直于弦的直径平分弦说法正确;
圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,故③说法不正确;
平分弦(不是直径)的直线也必平分弦所对的两条弧,故④说法不正确;
半圆的弧长是圆的弧长的一半,不是圆中最长的弧,故⑤说法不正确;
不在同一条直线上的三个点可以确定一个圆,故⑥说法正确,
∴不正确的语句有4个,
故选:B
6.如图是一个圆柱形输水管横截面的示意图,阴影部分为有水部分,如果水面AB的宽为8cm,水面最深的地方高度为2cm,则该输水管的半径为( )
A.3cmB.5cmC.6cmD.8cm
【答案】B
【详解】解:如图所示:过点O作OD⊥AB于点D,连接OA,
∵OD⊥AB,
∴AD=AB=4cm,
设OA=r,则OD=r﹣2,
在Rt△AOD中,OA2=OD2+AD2,即r2=(r﹣2)2+42,
解得r=5cm.
∴该输水管的半径为5cm;
故选:B.
7.如图,在⊙O中,弦AB⊥OC于E点,C在圆上,AB=8,CE=2,则⊙O的半径AO=___________.
【答案】5
【详解】解:设⊙O的半径为r,则OC=OA=r,OE=OC-CE=r-2,
∵OC⊥AB,AB=8,
∴AE=BE=AB=4,
在Rt△OAE中,由勾股定理得:42+(r-2)2=r2,
解得:r=5,
即⊙O的半径长为5,
故答案为:5.
8.如图,⊙O的直径AB的长是20,弦CD⊥AB,垂足为点E, CD=16,则CE=____,BE=_____.
【答案】 8 4
【详解】解:∵为直径,弦CD⊥AB,
∴,
连接,如下图:
由题意可得:
由勾股定理可得:
∴
故答案为:8,4
9.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
【答案】见解析
【详解】解:证明:作OH⊥AB于H,如图,
则AH=BH,
∵OC=OD,OH⊥AB,
∴CH=DH,
∴CH﹣AH=DH﹣BH,
即AC=BD.
10.如图所示,已知为⊙的直径,是弦,且于点,连接AC、OC、BC.
(1)求证:;
(2)若,,求⊙的直径.
【答案】(1)证明见解析;(2)10
【详解】(1)证明:∵
∴
又∵为直径,
∴,
又∵
∴,
∴
∴
(2)∵,为直径
∴,
∴
又∵,
∴,
∴,
∴,
∴在中,
即,解得,
∴.
题组B 能力提升练
1.一个圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD的长为( )
A.2mB.4mC.6mD.8m
【答案】B
【详解】∵CD垂直平分AB,
∴AD==8m
∴OD==6m
∴CD=OC﹣OD=10﹣6=4m
故选:B.
2.如图,的半径为,,经过点的的最短弦的长为( )
A.4B.6C.8D.10
【答案】C
【详解】解:如图,过点作弦,交于点、,连接;过点作弦,交于点、,过点作,连接,
∴,,
∴在中,,
∵在和中,,
,,
∴,
∴,
∴为过点的最短弦,
∵的半径为,,
∴在中,
,
∴,
∴经过点的的最短弦的长为.
故选:C.
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A.B.C.D.8
【答案】B
【详解】解:过点O作OE⊥AB于点E,
∵大圆和小圆的圆心都为点O,OE⊥AB,
∴AE=BE,CE=DE,
∵,
∴AE=BE=12,
∵OA=13,
∴,
设,
则CE=12-x,
在Rt△COE中,,
解得:,
即OC的长为,
故选:B.
4.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是()
A.∠COE=∠DOEB.CE=DE
C.OE=BED.
【答案】C
【详解】∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴,DE=CE,,
∴B,D选项正确;
∵,
∴,
∴∠COE=∠DOE,
∴A选项正确;
只有当∠COE=60°时,才有OE=BE.
∴C选项不成立;
故选:C.
5.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸B.24寸C.26寸D.28寸
【答案】C
【详解】解:设圆材的圆心为O,延长CD,交于点E,连接OA,如图所示:
由题意知:CE过点O,且,
则.
设圆形木材半径为r,
则,.
∵,
∴,
解得 ,
即的半径为13寸,
∴的直径为26寸.
故选:C.
6.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口的长度为( )
A.8mmB.6mmC.10mmD.0.9mm
【答案】A
【详解】解:如图,点O为圆心,过点O作OC⊥AB,
根据垂进定理可得:AC=BC,
∵直径是10mm,
∴OA=5mm,OC=8-5=3mm,
在Rt△AOC中,∠OCA=90°,
∴,
∴AB=2AC=8mm,
故选:A.
7.如图,M是⊙O内一点,已知过点M的⊙O最长的弦为20cm,最短的弦长为16cm,则OM=_______cm.
【答案】6
【详解】解:过点M的⊙O最长的弦就是直径,
∴BO=10cm,
最短的弦就是垂直于直径的弦,即BM=8cm.
所以利用勾股定理可得OM==6cm.
故答案为:6.
8.如图,点O是半圆的圆心,D是以AB为直径的半圆上的一点,以OD为对角线作正方形OCDE,经过C,E的直线分别与半圆弧交于F,G.已知CE=6,则FG的长为______.
【答案】
【详解】解:如图所示,连接OD交FG于H,连接OF,
∵四边形OCDE是正方形,
∴OD⊥CE,OD=CE=6,OD=2OH,
∴FG=2FH,OH=3,OF=OD=6,
∴,
∴,
故答案为:.
9.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
【答案】
【详解】解:连接OC,
∵EM过圆心,EM⊥CD,
∴CM=CD,
∵CD=4cm,
∴CM=2cm,
设圆的半径是xcm,
在Rt△COM中,OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
∴圆的半径长是cm.
10.如图,AB是圆O的直径,点C、D为圆O上的点,满足:,AD交OC于点E.已知OE=3,EC=2
(1)求弦AD的长;
(2)请过点C作AB的平行线交弦AD于点F,求线段EF的长.
【答案】(1)8;(2)
【详解】解:(1),得CO⊥AD,AE=DE.
在△AOE中,∠AEO=90°,OE=3,OA=OC=OE+CE=5,
得AE=,
所以AD=AE+DE=8;
(2)由CFAB,得,
则.
题组C 培优拔尖练
1.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块B.第二块C.第三块D.第四块
【答案】A
【详解】解:第一块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
2.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2B.C.D.
【答案】A
【详解】连接,过点,分别作于,于,则四边形是矩形,
,,
,
,
,
(HL),
,
则,
,
,
,
.
故选:A.
3.如图,矩形ABCD是由边长为1的五个小正方形拼成,O是第2个小正方形的中心,将矩形ABCD绕O点逆时针旋转90°得矩形,现用一个最小的圆覆盖这个图形,则这个圆的半径是( )
A.B.C.D.
【答案】C
【详解】作线段BC、的垂直平分线MH、NH,两线的交点为H点,连接BH,如图,
∵MH、NH为线段BC、的垂直平分线,
∴BM=BC=,==,
∴HM=-1=,
∴,
故选:C.
4.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A.B.4C.D.5
【答案】D
【详解】解:连接,过点作于点,如图所示,
则,,
∵PA=4,PB=6,
∴,
∴,
∴,
在中,,
在中,,
故选:D
5.如图,AC是的直径,弦于E,连接BC,过点O作于F,若,,则OE的长为( )
A.3B.4C.D.5
【答案】A
【详解】解:连接OB、AB,
中
故选:A.
6.如图,等腰梯形ABCD内接于半圆D,且AB=1,BC=2,则OA=( )
A.B.C.D.
【答案】A
【详解】解:如图,作BE⊥AD于E, OF⊥CB于F,连接OB,
在等腰梯形ABCD中,
∵OF⊥CB,
∴BF=BC=1,
∴OE=1,
设AE=x,
∵OA、OB是⊙O的半径,
∴OB=OA=x+1,
由勾股定理可知,AB2﹣AE2=OB2﹣OE2,即12﹣x2=(x+1)2﹣12,
整理得2x2+2x﹣1=0,
解得或(不合题意,舍去)
∴OA=AE+OE=+1=.
故选:A.
7.如图,在⊙O内有折线ABCO,点A、B在圆上,点C在⊙O内,其中AB=9,OC=3,∠B=∠C=60°,则BC的长为_____.
【答案】6
【详解】延长CO交AB于点D,过点O作OE⊥AB垂足为E,
因为∠B=∠C=60°,
所以∠BDC=60°,
所以△BDC是等边三角形,
所以BC=BD=CD,∠DOE=30°.
因为OE⊥AB,AB=9,
所以BE=AE=4.5.
设OD=x,OC=3
所以DE= ,BD=4.5+,CD=OC+DO=x+3,
所以4.5+=x+3,
解得x=3,
所以BC=CD=OC+OD=3+3=6,
故答案为:6.
8.如图, 在⊙O中,AB是⊙O的直径,,AB=8,M是AB上的一动点,CM+DM的最小值是_____________.
【答案】8
【详解】解:如图,作点C关于AB的对称点,连接D与AB相交于点M,则CM=M,
此时,点M为CM+DM的最小值时的位置,
由垂径定理,,
∴,
∵,AB为直径,
∴D为直径,
即CM+DM=D=AB,
∵AB=8,
∴CM+DM的最小值是8.
故答案为:8.
9.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D.
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
【答案】(1)见解析
(2)AC=
【详解】(1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE﹣DE=AE﹣CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE===2,
AE===4,
∴AC=AE﹣CE=4﹣2.
10.已知AB是半圆O的直径,OD⊥弦AC于D,过点O作交半圆O于点E,过点E作EF⊥AB于F.若AC=2,
(1)求OF的长;
(2)连接BE,若BE=,求半径OA的长.
【答案】(1)OF=1
(2)半径为3
【详解】(1)解:∵OD⊥AC,AC=2,
∴AD=CD=1,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EOF=90°,
∴∠DAO=∠EOF,
∵在△ADO和△OFE中,,
∴△ADO≌△OFE(AAS),
∴OF=AD=1.
(2)解:设OA=OB=OE= x,则:BF=OB-OF=x-1,
∵EF⊥AB,
∴∠BFE=∠OFE=90°,
∴,
∴,
解得:,(舍去)
∴半径OA=3.
课程标准
(1)理解圆的对称性;
(2)掌握垂径定理及其推论;
(3)学会运用垂径定理及其推论解决有关的计算、证明和作图问题.
人教版九年级数学上册同步精品讲义 第05课 根与系数的关系(原卷版+解析): 这是一份人教版九年级数学上册同步精品讲义 第05课 根与系数的关系(原卷版+解析),共23页。
人教版九年级数学上册同步精品讲义 第03课 公式法(原卷版+解析): 这是一份人教版九年级数学上册同步精品讲义 第03课 公式法(原卷版+解析),共28页。试卷主要包含了一元二次方程根的判别式是,表示,一元二次方程实数根的情况,一元二次方程实数根的情况判断△等内容,欢迎下载使用。
人教版九年级数学上册同步精品讲义 第02课 配方法(原卷版+解析): 这是一份人教版九年级数学上册同步精品讲义 第02课 配方法(原卷版+解析),共20页。试卷主要包含了直接开平方法的解读,方程x2=p的根的情况,配方,开方,求解等内容,欢迎下载使用。












