2024年中考数学压轴题专项练习—函数中的新定义问题

这是一份2024年中考数学压轴题专项练习—函数中的新定义问题，文件包含73函数中的新定义问题答案docx、73函数中的新定义问题docx等2份试卷配套教学资源，其中试卷共77页， 欢迎下载使用。

（2）已知点，，若等边，，顺时针排列）上的点均不是线段的“四象点”，求的取值范围；
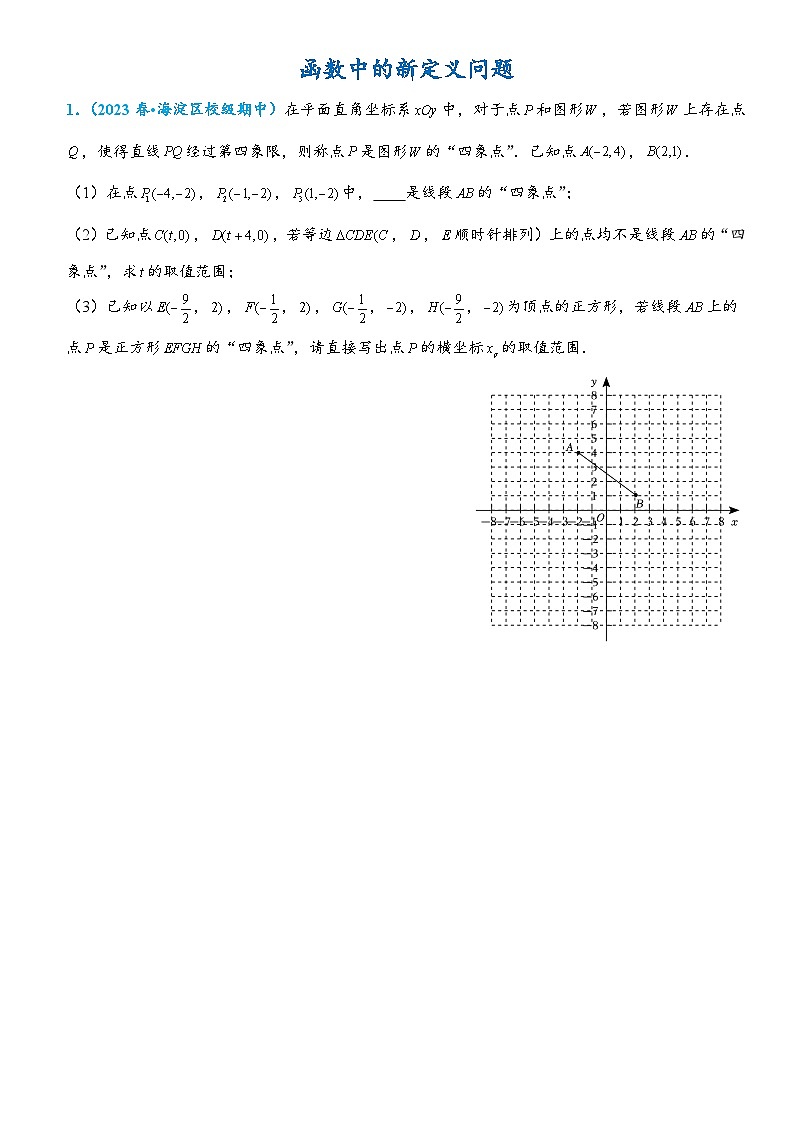
（3）已知以，，，，，，，为顶点的正方形，若线段上的点是正方形的“四象点”，请直接写出点的横坐标的取值范围．
【解答】解：（1）如图：
设直线的解析式为，
将，代入得，
解得：，
直线的解析式为，
故直线经过原点，
由函数图象可知，线段上不存在一点使得其与所在的直线经过第四象限；
，，
直线的解析式为，
直线经过第四象限，
是线段的四象点；
在第四象限，
是线段的四象点；
故答案为：，；
（2）如图：
，，是等边三角形，，顺时针排列），
点一定在轴下方，
又等边，，顺时针排列）上的点均不是线段的四象点，
点在第三象限，
如图所示，过点作于
，，
，则
，
是等边三角形，
，
，
点的纵坐标为，
由（1）得直线的解析式为，
当时，，
当直线恰好经过点时，点的坐标为，，
此时，
结合函数图象可知，当点继续向左移动的时候，等边，，顺时针排列）上的点均不是线段的四象点，向右移动的时候，等边，，顺时针排列）上存在一点是线段的四象点，
当等边，，顺时针排列）上的点均不是线段的四象点时，；
（3）如图：
，，
直线的解析式为，
，，
直线的解析式为，
令，
解得：，
，，
结合函数图象可知，当点右移动的时候，直线经过第四象限，即点是正方形的“四象点”，
若线段上的点是正方形的“四象点”，则点的横坐标的取值范围为．
2．（2023•婺城区模拟）定义：在平面直角坐标系中，直线与某函数图象交点记为点，作该函数图象中，点及点右侧部分关于直线的轴对称图形，与原函数图象上的点及点右侧部分共同构成一个新函数的图象，称这个新函数为原函数关于直线的“迭代函数“．例如：图1是函数的图象，则它关于直线的“迭代函数“的图象如图2所示，可以得出它的“迭代函数“的解析式为．
（1）写出函数关于直线的“迭代函数“的解析式为 ．
（2）若函数关于直线的“迭代函数“图象经过，则 ．
（3）已知正方形的顶点分别为：
，，，，其中．
①若函数关于直线的“迭代函数“的图象与正方形有3个公共点，则 ；
②若，函数关于直线的“迭代函数“的图象与正方形有4个公共点，则的取值范围为 ．
【解答】解：（1）如图1，设点为直线与函数的交点，点，
，点关于直线的对称点为，
设所在直线的解析式为：，
，
解得，
；
故答案为：；
（2）根据题意可得，关于直线的对称点在原抛物线上，
，
解得；
故答案为：；
（3）①如图，当正方形的边过点时，，此时正方形与此迭代函数有三个交点；
如图，当时，正方形与此迭代函数有四个交点，当继续增大，交点超过4个，不符合题意；
故答案为：3；
②如图，当时，此迭代函数与正方形有5个交点，
如图时，当时，此迭代函数与正方形有4个交点，符合条件；
如图时，当时，此迭代函数与正方形有4个交点，符合题意；
当时，此迭代函数与正方形有3个交点，其中一个交点坐标为；
如图，当时，此迭代函数过点，迭代函数与正方形有5个交点，
当时，迭代函数与正方形有5个交点，符合题意；
故答案为：或或．
3．（2023•开福区校级一模）对某一个函数给出如下定义，当自变量满足，为实数，时，函数有最大值，且最大值为，则称该函数为理想函数．
（1）当，时，在①；②中， ② 是理想函数；
（2）当时，反比例函数是理想函数，求实数的值；
（3）已知二次函数是理想函数，且最大值为．将该函数图象向左平移个单位长度所得图象记为，若图象的顶点为，与轴交于，在的左侧），与轴交于点，点，分别为的外心和内心，求以为边长的正方形面积．
【解答】解：（1）①，，随的增大而增大，当时，最小值为，
最大值为，则，故①不是理想函数；
②，，随的增大而减小，当时，最小值为，最大值为，则，故②是理想函数；
故答案为：②；
（2），
，
．
当时，，当时，随着的增大而减小，
则当时，最大值为6，
，即．
当时，，当时，随着的增大而增大，
则当时，最大值为，
，即，此方程无实根．
当时，，函数没有最大值，不合题意，舍去．
综上所述，的值为；
（3）最大值为，
，即，
，
，
，即，
此时，
对称轴为直线，
当，即时，则当时，取最大值，
，
，不合题意，舍去，
当，即时，
①若，即时，则当时，取最大值．
，解得不合题意，舍去），
②，即时，则当时，取最大值，
，，不合题意，舍去；
综上，的值为，
，则图象的解析式为：，
图象的顶点为，与轴交于，在的左侧），与轴交于点，
，，，
，，，
，
是直角三角形，且，
如图，点是的外心，
点是的中点，
，
点是的内心，即点是内切圆圆心，
，
，
，
，
．
即以为边长的正方形面积为．
4．（2023•门头沟区一模）在平面直角坐标系中，已知图形上的两点，（点，不重合）和另一点，给出如下定义：连接，，如果，则称点为点，的“条件拐点”．
（1）如图1，已知线段上的两点，．
①点，，中，点，的“条件拐点”是 点和点 ；
②如果过点且平行于轴的直线上存在点，的“条件拐点”，求的取值范围；
（2）如图2，已知点，，过点作直线轴，点，在直线上，且．如果直线上存在点，的“条件拐点”，直接写出的取值范围．
【解答】解：（1）①，，
，
当点时，
则，，
，即，
，
，
点是点，的“条件拐点”；
当点时，
则，，
，即，
，即与不垂直，
点不是点，的“条件拐点”；
当点时，
则，，
，即，
，
，
点是点，的“条件拐点”；
故答案为：点和点；
②根据①可得：，
，
，
如图所示：点在以的中点为圆心，以为半径的圆上，
过点且平行于轴的直线上存在点，的“条件拐点”，
如图所示，点到此直线的距离，
点是的中点，且，，
点的坐标为，
，
解得：；
（2）在直线中，当时，，当时，，
，，
，
，，在以点为圆心，为半径的圆上，
分三种情况：
①当时，如图2，过点作于，则，，
是等腰直角三角形，
，
直线上存在点，的“条件拐点”，
，
，
；
②当时，如图3，过点作于，则，，
直线上存在点，的“条件拐点”，
，
，
；
③当时，如图4，过点作于，则，，
直线上存在点，的“条件拐点”，
，
，
；
④当时，如图5，过点作于，则，，
直线上存在点，的“条件拐点”，
，
，
；
综上，的取值为或．
5．（2023•苏州二模）定义：若存在实数对坐标同时满足一次函数和反比例函数，则二次函数为一次函数和反比例函数的“生成”函数．
（1）试判断（需要写出判断过程）：一次函数和反比例函数是否存在“生成”函数，若存在，写出它们的“生成”函数和实数对坐标．
（2）已知：整数，，满足条件，并且一次函数与反比例函数存在“生成”函数，求的值．
（3）若同时存在两组实数对坐标，和，使一次函数和反比例函数为“生成”函数，其中，实数，，设，求的取值范围．（注：一元二次方程的求根公式为
【解答】解：（1）联立，
解得或．
则一次函数和反比例函数存在“生成”函数，
它们的“生成”函数为，实数对坐标为，；
（2）根据题意得：
，
解得：．
，
，
解得，
，
，
．
是整数，
；
（3），，
，，，，
，，
方程有两个不相等的实根．
由题意可知：、是方程的两个不等实根，
，，
，
，
．
6．（2023•西城区校级模拟）在平面直角坐标系中，我们给出如下定义：将图形绕直线上某一点顺时针旋转，再关于直线对称，得到图形，我们称图形为图形关于点的二次关联图形．已知点．
（1）若点的坐标是，直接写出点关于点的二次关联图形的坐标 ；
（2）若点关于点的二次关联图形与点重合，求点的坐标（直接写出结果即可）；
（3）已知的半径为1，点关于点的二次关联图形在上且不与点重合．若线段，其关于点的二次关联图形上的任意一点都在及其内部，求此时点坐标及点的纵坐标的取值范围．
【解答】解：（1）如图1，根据二次关联图形的定义分别找到和，过点作轴于点，
，
由旋转可知，，，
，
，
，
，，
，
；
故答案为：；
（2）分析可知，点在轴的下方，设点的纵坐标为，
如图2，过点作轴于点，过点作轴交于点，
由（1）知，
，，
，
由题意可知，点与点关于直线对称，
，，
解得，
；
（3）由（2）知，
，
点在上，
，
解得（舍或；
，如图3，
线段，
点在以点为圆心，1为半径的圆上，
若其关于点的二次关联图形上的任意一点都在及其内部，如图3，可知点是一个临界点，
连接，
，
△是等边三角形，
过点作轴于点，则，，
，，
，，
，，
由对称性可知，另外一点的坐标为，，
的取值范围为：．
7．（2022春•慈溪市校级期中）【学习新知】如果关于的一元二次方程有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”．
研究发现了此类方程的一般性结论：设其中一根为，则另一个根为，因此，所以有．
我们记“”，即时，方程为倍根方程．
【问题解决】
（1）方程①；②；③；④，这几个方程中，是倍根方程的是 ②④ （填序号即可）；
（2）若是倍根方程，求的值；
（3）关于的一元二次方程是倍根方程，且点在一次函数的图象上，求此倍根方程的表达式并求出方程的解．
【解答】解：（1）在方程①中，；
在方程②中，；
在③中，；
在④，，
②④是倍根方程，
故答案为：②④；
（2）整理得：，
是倍根方程，
，
；
（3）是倍根方程，
，
整理得：．
在一次函数的图象上，
，
，，
此方程的表达式为．
8．（2022春•顺义区校级月考）在平面直角坐标系中，对于点和线段，我们定义点关于线段的线段比．
（1）已知点，，．
①点关于线段的线段比 ；
②点关于线段的线段比 ；
③点关于线段的线段比，求的值．
（2）已知点，点，直线与坐标轴分别交于，两点，若线段上存在点使得这一点关于线段的线段比，直接写出的取值范围．
【解答】解：（1）①，，，
，，，
，
；
故答案为：；
②，，，
，，，
，
；
故答案为：；
③，，，
，，
当时，，即，
由关于线段的线段比可得：
，解得或（舍去），
，
当时，，即，
由关于线段的线段比可得：
，
解得（舍去）或，
，
综上所述，点关于线段的线段比，或；
（2）直线与坐标轴分别交于，两点，
，，
点，点，
，在右边2个单位，
当线段上的点到距离较小时，分两种情况：
①当、在点左侧时，如图：
线段上存在点使得这一点关于线段的线段比，
，即，
解得：；
②当在右侧，在左侧时，过作于，如图：
线段上存在点使得这一点关于线段的线段比，
，即，
，
而，，
，
是等腰直角三角形，
，
，即，
解得，
线段上存在点使得这一点关于线段的线段比，线段上的点到距离较小时，，
当线段上的点到距离较小时，也分两种情况：
①当在右侧，在左侧时，如图：
线段上存在点使得这一点关于线段的线段比，
，即，
解得，
②当、在点右侧时，过作于，如图：
线段上存在点使得这一点关于线段的线段比，
，即，
，
而，，
，
是等腰直角三角形，
，
，即，
解得：，
线段上存在点使得这一点关于线段的线段比，线段上的点到距离较小时，；
综上所述，线段上存在点使得这一点关于线段的线段比，则或．
9．（2022春•海淀区校级期中）在平面直角坐标系中，对于任意两点，与，的“非常距离”，给出如下定义：
若，则点与点的“非常距离”为；
若，则点与点的“非常距离”为．
例如：点，点，因为，所以点与点的“非常距离”为，也就是图1中线段与线段长度的较大值（点为垂直于轴的直线与垂直于轴的直线的交点）．
（1）已知点，，为轴上的一个动点，
①若点与点的“非常距离”为2，写出一个满足条件的点的坐标；
②直接写出点与点的“非常距离”的最小值；
（2）已知点是直线上的一个动点，
①如图2，点的坐标是，求点与点的“非常距离”的最小值及相应的点的坐标；
②如图3，正方形的边长为1，边在轴上运动，点的横坐标大于等于，点是正方形边上的一个动点，直接写出点与点的“非常距离”的最小值及相应的点和点的坐标．
【解答】解：（1）①为轴上的一个动点，
设点的坐标为．
，
，
解得或；
点的坐标是或；
故答案为：或；
②点与点的“非常距离”的最小值为．
故答案为：．
（2）①如图2，取点与点的“非常距离”的最小值时，
根据运算定义“若，则点与点的“非常距离”为”知：．即，
由题意可知，点是直线上的一个动点，点的坐标是，
设点的坐标为，
，
此时，，
点与点的“非常距离”的最小值为：，
此时，；
②如图3，根据“非常距离”的定义可知，当点与重合，且点与点重合时，，的“非常距离”最小，且，
此时，，
，解得，
．
此时，点的坐标为，，“非常静距离”的最小值为．
综上，与点的“非常距离”的最小值为；相应的点的坐标为，点的坐标，．
10．（2022秋•东城区校级期中）对于点，与图形，如果图形上存在一点，，使得当时，，则称点为图形的一个“近卫点”．
（1）已知，，在点，，，中，是线段的“近卫点”的有 ， ；
（2）以原点为圆心，1为半径作，直线与轴、轴分别交于、两点，若线段上任意一点都是的“近卫点”，求的取值范围；
（3）已知点，以点为中心的正方形满足以下条件：四条边都平行于坐标轴，且边长为1．若正方形上存在抛物线的“近卫点”，直接写出的取值范围．
【解答】解：（1），，
线段轴，
设线段上存在点，，使时，，
，，
，是线段的“近卫点”，
故答案为：，；
（2）线段上任意一点都是的“近卫点”，
线段在是圆的弦，
圆的半径是1，
；
（3）点是正方形的中心，正方形的边长为1，
，，，，，，，，
设正方形上点是抛物线的“近卫点”，抛物线上存在点使得当时，，
当点在轴右侧时，，
如图1，当点与点重合时，，，
，
解得或（舍去），
如图2，当点与点重合时，，，
，
解得或（舍去），
时，正方形上存在抛物线的“近卫点”；
当点在轴的左侧时，，
如图3，当点与点重合时，，，
，
解得（舍去）或，
如图4，当点与点重合时，，，
，
解得（舍去）或，
时，正方形上存在抛物线的“近卫点”；
综上所述：或时，正方形上存在抛物线的“近卫点”．
11．（2022秋•大兴区期中）在平面直角坐标系中，已知四边形是平行四边形，点，，点的纵坐标为，点是边上一点，连接，将线段绕点逆时针旋转得到线段．
给出如下定义：
如果抛物线同时经过点，，则称抛物线为关于点，的“伴随抛物线”．
（1）如图1，当点与点重合时，点的坐标为 ，此时关于点，的“伴随抛物线”的解析式为 ；
（2）如图2，当点在边上运动时，连接．
①当取最小值时，求关于点，的“伴随抛物线”的解析式；
②若关于点，的“伴随抛物线” 存在，直接写出的取值范围．
【解答】解：（1）如图，连接，过点作作轴的垂线于点，过点作轴于点，
，
，
，
由旋转可知，，，
是等边三角形，
，
，，
．
将，代入抛物线，
，
解得．
抛物线的解析式为：；
故答案为：；；
（2）①由旋转可知，点在线段上运动，过点作于点，点即为所求，过点作轴的垂线，过点作轴的垂线，交于点，交轴于点，
由题意可知，，
由旋转可知，△，
，，
，
，，
，，
，，
，．
将，，代入抛物线，
，
解得．
关于点，的“伴随抛物线”的解析式为：．
②如图，过点作轴的平行线，交于点，
，，
，，
将，，代入抛物线的解析式，
，
解得．
抛物线的解析式为：．
结合图象可知，的取值范围为：；．
12．（2022•滨海县模拟）如图1，直线与、轴分别相交于、两点，将绕点逆时针旋转得到，过点、、的抛物线叫做直线的关联抛物线，而直线叫做抛物线的关联直线．
（1）已知直线，求直线的关联抛物线的表达式；
（2）若抛物线，求它的关联直线的表达式；
（3）如图2，若直线，为中点，为中点，连接，为中点，连接．若，求直线的关联抛物线的表达式；
（4）在（3）的条件下，将直线绕着点旋转得到新的直线，若点，与点，分别是抛物线与直线上的点，当时，，请直接写出的取值范围．
【解答】解：（1），
当时，，
；
当时，即，解得，
，
由旋转的性质可知，，
．
设的解析式为，
则，
解得：，
；
（2），
令，即，
解得，，
，，
有旋转的性质可知，．
，
设的解析式为，
则，
解得，
；
（3）连接、，有旋转的性质可知，，
是等腰直角三角形，
又，
，
在中，，
在中，，
，
，当时，，
点，即．
由旋转的性质可知，，
点．
在中，，
，
设的解析式为，
则，
解得，
；
（4）由旋转的性质可知，．
，
经过点，
，即．
根据题意可知，当时，，
分析与的位置关系可知，只需当时，即可，
，即，
，
解得：．
的取值范围是：．
13．（2022春•海淀区期末）在平面直角坐标系中，已知的顶点，，对于点和，给出如下定义：如果上存在三个点，使得以点和这三个点为顶点的四边形是平行四边形，则称点是的“平行连接点”．例如，图1中，，两点的坐标分别为，，上存在，和三个点，使得四边形是平行四边形，故点是的“平行连接点”．
（1）如图2，当点的坐标为时，
①点，，，中，是的“平行连接点”的是 ， ．
②若是的“平行连接点”，请在图2中画出一个以点和上的三个点为顶点的平行四边形，这个平行四边形对角线交点的纵坐标为 ，的取值范围为 ．
（2）如图3，当点的坐标为时，直线上存在的“平行连接点”，则的取值范围为 ．
【解答】解：（1）①由图可知，，，
，，，能组成平行四边形，
是的“平行连接点”，
，，，能组成平行四边形，
是的“平行连接点”，
故答案为：．；
②如图2中，
当时，且，满足题意；
当时，上一定存在点，使得是平行四边形，满足条件；
当时，上存在一点，使得是平行四边形，满足条件，
的取值范围为：，
故答案为：1，；
（2）如图3中，当直线与图中阴影部分有交点时（不包括点，点，满足条件
当直线经过点时，，解得，
当直线经过点时，，解得，
观察图象可知，满足条件的的值或．
故答案为：或．
14．（2022春•大兴区期末）对于平面直角坐标系中的点和四边形，给出如下定义：若在四边形上存在一点，使得，两点间的距离小于或等于1，则称为四边形的“关联点”．
如图，已知点．
（1）在点，，中，四边形的关联点是 ， ；
（2）点为直线上一点．
①若直线过点，点是四边形的关联点，求点的横坐标的取值范围；
②若直线上，不存在点是四边形的关联点，直接写出的取值范围．
【解答】解：（1）在坐标系中找到，，三点，如图所示：
故答案为：，．
（2）①直线过点，
，
解得．
直线，
令，则．
直线与轴的交点为，．
，，
直线的解析式为：．
，
如图，分别过点，作的垂线，垂足分别为，，
，
四边形为平行四边形，
，
，
平行四边形为矩形，
，
，
，
是等边三角形，，
，
，
，
，，
由平移可知，．
综上，．
②直线，
令，
，
直线过定点，．
由①知，当时，存在点是四边形的关联点，
由对称性可知，当时，存在点是四边形的关联点，
当且时，不存在点是四边形的关联点．
15．（2022春•武侯区校级月考）如图1，在平面直角坐标系中，已知抛物线与轴交于点，两点，与轴交于点．
（1）求抛物线解析式；
（2）如图2，作出如下定义：对于矩形，其边长，为常数，且，其矩形长和宽所在直线平行于坐标轴，矩形可以在平面内自由的平移，且所在直线与抛物线无交点，则称该矩形在“游走”，每一个位置对应的矩形称为“悬浮矩形”；对与每一个“悬浮矩形”，若抛物线上有一点，使得的面积最小，则称点是该“悬浮矩形”的核心点．
①请说明“核心点” 不随“悬浮矩形”的“游走”而变化，并求出“核心点” 的坐标（用表示）；
②若，所在直线与抛物线交于点和在的右侧），是否存在这样的“悬浮矩形”，使得是直角三角形，若存在，并求出“悬浮矩形”中对角线所在直线的表达式；若不存在，说明理由．
【解答】解：抛物线与轴交于点，两点，与轴交于点．
把，，代入得：
，
解得．
抛物线的解析式为：．
（2）①过抛物线上点作直线的平行线，的面积乘以点到直线的距离，当点到直线距离最短时，的面积最小，由图象可知，当过点的直线与抛物线只有一个交点时，点到直线距离最短，这样的点只有一个，
“核心点” 不随“悬浮矩形”的“游走”而变化；
，，
所在直线的解析式可设为：，
过点与直线平行的直线解析式为：，
令，得，
过点的直线与抛物线只有一个交点，
△，可得，
，解得，
，
；
②当时，，
设直线的解析式为：，
令，得，
解得或，
所在的直线与抛物线交于点，，
△，即，
点在点的右侧，
，，，，
，
，
，
当时，，
解得或，
直线的解析式为：或；
当时，，
解得或，
直线的解析式为：或；
当时，，
无解；
综上，直线的解析式为：或或．
16．（2021•镜湖区校级自主招生）我们把一个函数图象上横坐标与纵坐标相等的点称为这个函数的不动点．
（1）求函数的不动点；
（2）若函数有两个关于原点对称的不动点，，求的值及函数的不动点；
（3）已知函数．
①当，时，求函数的不动点；
②若对任意实数，函数恒有两个相异的不动点，求的取值范围．
【解答】解：（1）令，解得，，
函数的不动点为；
（2）令，得：，
即，
设方程的两根为，，则两个不动点，，，，
由于它们关于原点可以得到对称为，所以，
，
解得：，
方程为，
解得：，
两个不动点，，，；
（3）①当，时，，
由题意得：，解得：或，
即函数的“不动点”为，；
②由题意得：，
化简得：，即该式恒有两个不同的实数根，
△恒成立，
，上式横成立，则△，
解得：．
17．（2021•海沧区模拟）已知抛物线与轴交于点，与轴交于点和（点在点左侧），若是等腰三角形，则称抛物线是“理想抛物线”．
（1）判断抛物线是否为“理想抛物线”，并说明理由；
（2）已知经过点的抛物线是“理想抛物线”．
①若点，，是抛物线上另两点，满足当时，与的交点始终在抛物线的对称轴上，且线段的垂直平分线恰好经过点，求此抛物线的解析式；
②是否存在整数使得，且？若存在，求出所有满足条件的整数的值；若不存在，请说明理由．
【解答】解：（1）抛物线是“理想抛物线”，理由如下：
抛物线的对称轴为直线：，
该抛物线是关于轴对称，则点、关于轴对称，
垂直平分，
为等腰三角形，
是为“理想抛物线”；
（2）①要满足是等腰三角形，则可能为底边，也可能为腰；
当为底边时，，点、关于轴对称，
此时，，
当时，，，
，，
的垂直平分线恰好经过点，
，
又是等腰三角形，
，
是等边三角形；
又，
，
；
抛物线的交点式为：，
把点坐标代入，．
（负值舍去），
此时抛物线的解析式为：；
当为腰时，，仍满足，，
，，
，，
必有点在点上方，则，
对称轴直线，
，
，
，，，
又，得，；
此时抛物线的解析式为：；
②存在整数使得，理由如下：
是的高，且，开口向上，抛物线与轴有两个交点，
，
，
，
，
解得，
则需要分两种情况，当时，，此时，
，解得，
，
，即，
此时，存在或或或满足题意；
当时，，此时，，
，解得，
，
，即，
此时，存在或满足题意；
综上可知，存在整数是使得，且，此时的值为或或或或1或2．
18．（2021•渝北区校级开学）如图①，定义：直线与、轴分别相交于、两点，将绕着点逆时针旋转得到，过点、、的抛物线叫做直线的“纠缠抛物线”，反之，直线叫做的“纠缠直线”，两线“互为纠缠线”．
（1）若，则纠缠抛物线的函数解析式是 ．
（2）判断并说明与是否“互为纠缠线”．
（3）如图②，若纠缠直线，纠缠抛物线的对称轴与相交于点，点在上，点在的对称轴上，当以点、、、为顶点的四边形是以为一边的平行四边形时，求点的坐标．
【解答】解：（1）若，
当时，；当时，，
点、、、的坐标分别为：、、、，
设纠缠抛物线的函数解析式为：，
将点的坐标代入上式得：，
解得：，
纠缠抛物线的函数解析式为：，
故答案为：；
（2）同（1）得：点、、、的坐标分别为：、、、，
设纠缠抛物线的函数解析式为：，
将点的坐标代入上式得：，
解得：，
纠缠抛物线的函数解析式为：，
与是“互为纠缠线”；
（3）同（1）得：点、、、的坐标分别为：、、、，
同理可得：纠缠抛物线的函数解析式为：，
则抛物线的对称轴为：，
设点，点，
将点、的坐标代入一次函数表达式并求得：
直线的表达式为：，
点的横坐标为，
点的纵坐标为，
点、横坐标差为1，纵坐标差为，
以点、、、为顶点的四边形是以为一边的平行四边形时，
由题意得：，即：，
解得：或，
当时，点，则点；
同理当时，点；
综上，点坐标为：或．
19．（2019春•西湖区校级月考）新定义的函数中，在关于的函数中，若时，函数有最大值和最小值，分别记和，且满足，则我们称函数为“最值型函数”．
（1）写出实数的其中一个值，使得函数为“最值型函数”，并说明理由；
（2）判断函数是否为“最值型函数”，并说明理由；
（3）是否存在实数使得函数是“最值型函数”，若存在则求出满足条件的的取值范围，若不存在说明理由．
【解答】解：（1）函数在时，随的增大而增大，
当，；，，
为“最值型函数”，
，
；
可以取3；
（2）如图，函数是“最值型函数”，理由如下：
，
对称轴为直线，，
当时，，当时，，
，，
函数是否为“最值型函数”；
（3）不存在，是“最值型函数”，
，
对称轴为直线，
①当时，当，，
当，，则，解得，
无解；
②当，当，，当，，
则，无解；
③当，当，，当，，
则，
解不等式组得：，
此种情况无解；
④当，当，，，，
则，
解得：，
此种情况无解；
综上所述不存在实数使得函数是“最值型函数”．
20．（2017秋•雨花区校级期末）定义：若存在实数对坐标同时满足一次函数和反比例函数，则二次函数为一次函数和反比例函数的“联姻”函数．
（1）试判断（需要写出判断过程）：一次函数和反比例函数是否存在“联姻”函数，若存在，写出它们的“联姻”函数和实数对坐标．
（2）已知：整数，，满足条件，并且一次函数与反比例函数存在“联姻”函数，求的值．
（3）若同时存在两组实数对坐标，和，使一次函数和反比例函数为“联姻”函数，其中，实数，，设，求的取值范围．
【解答】解：（1）联立，
解得或．
则一次函数和反比例函数存在“联姻”函数，
它们的“联姻”函数为，实数对坐标为，；
（2）根据题意得：，
解得．
，
解得，
，
，
．
是整数，
；
（3），，
，，，，
，，
方程有两个不相等的实根．
由题可得：、是方程即的两个不等实根．
，，
，
，
．
21．（2018秋•海淀区校级月考）在平面直角坐标系中，对于点和点，给出如下定义：
若，则称点为点的限变点．例如：点的限变点的坐标是，点的限变点的坐标是，点的限变点的坐标是．
（1）①点，的限变点的坐标是 ， ；
②在点、中有一个点是双曲线上某一个点的限变点，这个点是 ；（填“”或“”
（2）若点在函数的图象上，其限变点的纵坐标的取值范围是，求的取值范围；
（3）若点在关于的二次函数的图象上，其限变点的纵坐标的取值范围是或，其中．令，求关于的函数解析式及的取值范围．
【解答】解：（1）①点，的横坐标
其限变点纵坐标取其绝对值，即1
限变点的坐标为，
故答案为：，．
②时，，点的限变点为，不是点，
时，，点的限变点为，即点，
故答案为：．
（2）依题意，图象上的点的限变点必在函数的图象上（如图．
当时，取最小值，，
当时，或，或，
当时，．，．
，
由图象可知，的取值范围时：，
（3），
顶点坐标为．
图象上的点的限变点必在函数的图象上．
Ⅰ．若，如图2，的取值范围是或，与题意不符．
Ⅱ．若，如图3，当时，的最小值为，即；
当时，的值最大值，即．
．
关于的函数解析式为，，
当时，取最小值4，
的取值范围是．
Ⅲ．若，如图4，当时，的最小值为0，即；
当时，的值最大值，即．
．
关于的函数解析式为，，
当时，取最小值5，
综上所述：，
当时，的取值范围是．
当时，的取值范围是．
22．（2018春•雨花区校级月考）对于直线，有如下定义：我们把直线称为它的“姊线”，若与、轴分别相交于、两点，与、轴分别相交于、两点，我们把经过点、、的抛物线叫做的“母线”．
（1）若直线的“母线”为，求、的值；
（2）如图，若，为中点，为中点，连接，为中点，连接，若，求出的“姊线” 与“母线” 表示的函数解析式；
（3）将的“姊线”绕着点旋转得到新的直线，若点与点分别是“母线” 与直线上的点，当时，，求的取值范围．
【解答】解：（1）对于抛物线，令，得到，
，
令，得到，解得或2，
，，
经过、，
，
解得．
（2）如答图2所示，连接、．
点、为斜边中点，
，．
由题意，的“姊线” 为
可得：，，，，，，
，，
，
，
，，
，
，，
，，
，
，
，
，
为等腰直角三角形．
点为中点，
为等腰直角三角形，
，
，
，
，，
，．
的“姊线” 为，“母线” 表示的函数的解析式为．
（3）的“姊线”的解析式为，“母线” 的解析式为，
直线，
当时，，
不妨设，则，，
由题意，
解得或，
满足条件的是取值范围为：．
23．（2018秋•任城区校级期中）小明在课外学习时遇到这样一个问题：
定义：如果二次函数，，，是常数）与，，，是常数）满足，，，则称这两个函数互为“旋转函数”．
求函数的“旋转函数”．
小明是这样思考的：由函数可知，，，，根据：，，，求出、、，就能确定这函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）写出函数的“旋转函数”；
（2）若函数与互为“旋转函数”，求；
（3）已知函数的图象与轴交于点、两点，与轴交于点，点、、关于原点的对称点分别是、、，试证明经过点、、的二次函数与函数互为“旋转函数”．
【解答】解：（1）由函数可知，，．
由，，，得
，，．
函数的“旋转函数”为；
（2）由与互为“旋转函数“，得
，．
解得，．
当，时，；
（3）当时，，解得，，
，．
当时，，即．
由点，，关于原点的对称点分别是，，，得
，，．
设过点，，的二次函数，将，，代入，得
，
解得，
过点，，的二次函数．
函数可知，，．
由，，，得，，．
的“旋转函数”为．
经过点，，的二次函数与函数互为“旋转函数”．
24．（2017•北京模拟）在平面直角坐标系中，对于任意三点，，的“矩面积”，给出如下定义：
“水平底” ：任意两点横坐标差的最大值，“铅垂高” ：任意两点纵坐标差的最大值，则“矩面积” ．
例如：三点坐标分别为，，，则“水平底” ，“铅垂高” ，“矩面积” ．
（1）已知点，，．
①若，，三点的“矩面积”为12，求点的坐标；
②直接写出，，三点的“矩面积”的最小值．
（2）已知点，，，，其中，．
①若，，三点的“矩面积”为8，求的取值范围；
②直接写出，，三点的“矩面积”的最小值及对应的取值范围．
【解答】解：（1）由题意：．
①当时，，
则，可得，故点的坐标为；
当时，，
则，可得，故点的坐标为；
②根据题意得：的最小值为：1，
，，三点的“矩面积”的最小值为4；
（2）①，，三点的“矩面积”为8，
，，
．
．
，
；
②当时，，，此时，
当时，取最小值，；
当时，，，此时；
当时，，，此时，
当时，取最小值，；
，，三点的“矩面积”的最小值为16，此时的取值范围为．
25．（2017秋•河南月考）新定义：如图1，若抛物线的顶点在抛物线上，抛物线的顶点在抛物线上（点与点不重合），我们把这样的两条抛物线、互称为“友好”抛物线，可见一条抛物线的“友好”抛物线可以有多条．
解决问题：如图2，已知抛物线经过点，，且与轴交于点，点关于抛物线的对称轴对称的点为点．
（1）分别求出点的坐标和抛物线的解析式；
（2）求出以点为顶点的的“友好”抛物线的解析式，并指出与中同时随增大而增大的自变量的取值范围．
【解答】解：（1）抛物线经过点，，
其对称轴为：，
，
，，
抛物线与轴交于点，
，
抛物线的解析式为：；
（2）如图2，由题意可知：的“友好”抛物线的顶点，
设抛物线的解析式为：，
，
抛物线的顶点为，
抛物线的和互为友好抛物线，
过点，
，
，
抛物线的解析式为：，
由图象可知当时，与中同时随增大而增大．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/10/3 1:46:22；用户：微信用户；邮箱：rFmNt0ALlhXWmlRPd3BByUm_TL4@；学号：47883804