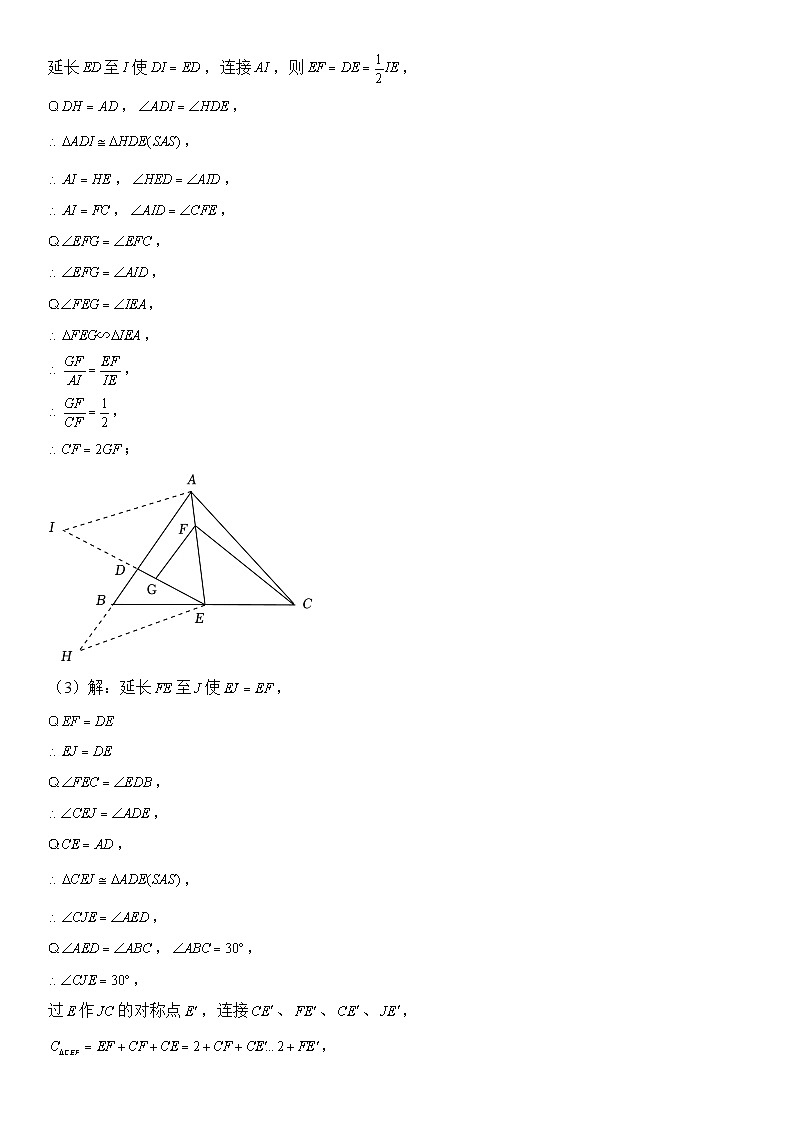
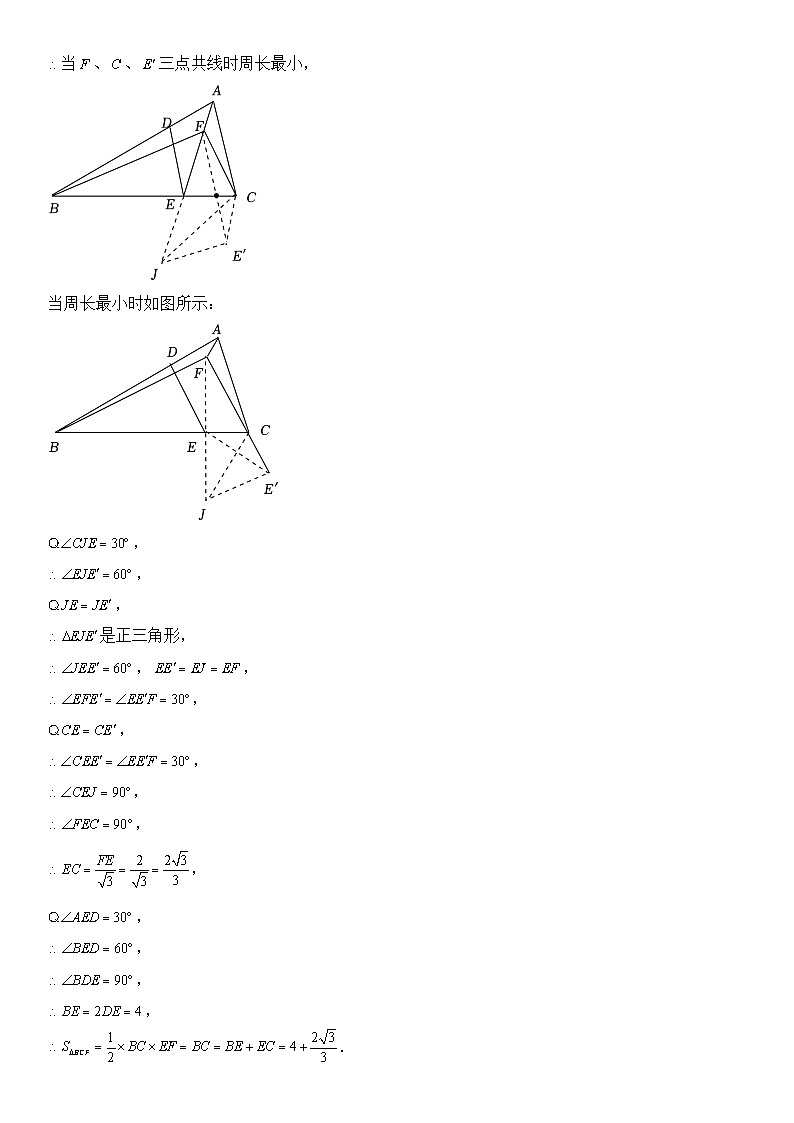
2024年中考数学压轴题专项练习—倍长中线

这是一份2024年中考数学压轴题专项练习—倍长中线，文件包含43倍长中线答案docx、43倍长中线docx等2份试卷配套教学资源，其中试卷共62页， 欢迎下载使用。

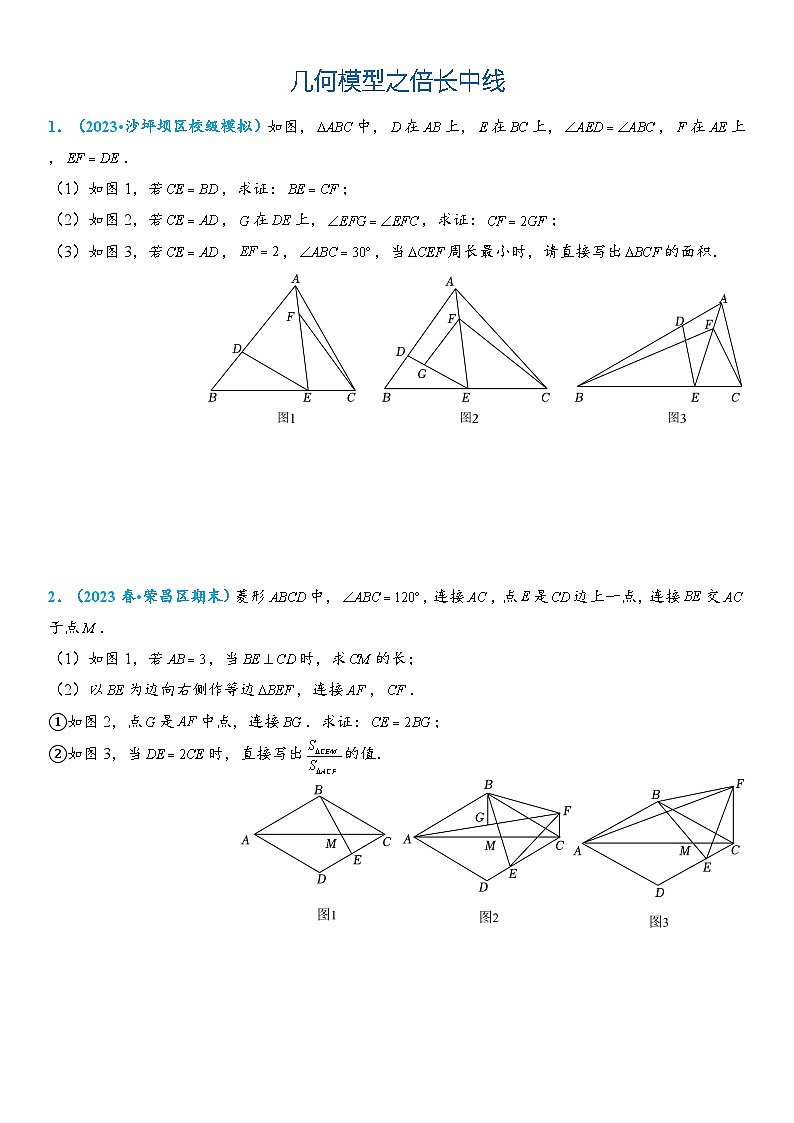
（1）如图1，若，求证：；
（2）如图2，若，在上，，求证：；
（3）如图3，若，，，当周长最小时，请直接写出的面积．
2．（2023春•荣昌区期末）菱形中，，连接，点是边上一点，连接交于点．
（1）如图1，若，当时，求的长；
（2）以为边向右侧作等边，连接，．
①如图2，点是中点，连接．求证：；
②如图3，当时，直接写出的值．
3．（2023•抚州三模）课本再现：
（1）我们研究平行四边形时，常常把它分成几个三角形，利用三角形全等的性质研究平行四边形的有关问题，同时也可以利用平行四边形研究三角形的有关问题，如探究三角形中位线的性质．
如图（1），在中，点，分别是，的中点，连接．则与的关系是 ．
定理证明
（2）请根据（1）中内容结合图（1），写出（1）中结论的证明过程．
定理应用
（3）如图（2），在四边形中，点，，分别为，，的中点，，的延长线交于点．若，则的度数是 ．
（4）如图（3），在矩形中，，，点在边上，且．将线段绕点旋转一定的角度，得到线段，点是线段的中点，求旋转过程中线段长的最大值和最小值．
4．（2023春•巴南区期中）在矩形中，是边上一点．
（1）若，平分，且，求的面积；
（2）若是中点且，于点，求证：；
（3）若，于点，连接并反向延长至点使得．点在直线上方，连接、，，，请探究并请直接写出与的数量关系．
5．（2023春•碑林区校级期中）为了进一步探究三角形中线的作用，数学兴趣小组合作交流时，小丽在组内做了如下尝试：如图1，在中，是边上的中线，延长到，使，连接．
【探究发现】（1）图1中与的数量关系是 ，位置关系是 ；
【初步应用】（2）如图2，在中，若，，求边上的中线的取值范围．（提示：不等式的两边都乘或除以同一个正数，不等号的方向不变．例如：若，则．
【探究提升】（3）如图3，是的中线，过点分别向外作、，使得，，延长交于点，判断线段与的数量关系和位置关系，请说明理由．
6．（2022秋•南沙区校级期末）如图，在中，点是的中点，分别以，为腰向外作等腰三角形和等腰三角形，其中，，，，，连接．
（1）请写出与的数量关系，并说明理由．
（2）延长交于点，求的度数．
7．（2023•蜀山区校级一模）如图，在中，，，于点，点是的中点，连接．
（1）若，，求的长；
（2）求证：；
（3）求证：．
8．（2021秋•东城区期末）如图，在等边三角形中，点为内一点，连接，，，将线段绕点顺时针旋转得到，连接，．
（1）用等式表示与的数量关系，并证明；
（2）当时，
①直接写出的度数为 ；
②若为的中点，连接，用等式表示与的数量关系，并证明．
9．（2022春•南岗区校级月考）在中，，点为的中点，点、分别在边、上，且满足．
（1）如图1，当时，若，，则 ；
（2）如图2，当时，求证：；
（3）如图3，当时将沿翻折，边与交于点，若，，求的长．
10．（2022•淮安二模）【问题情境】
学完《探索全等三角形的条件》后，老师提出如下问题：如图①，中，若，，求边上中线的取值范围．通过分析、思考，小丽同学形成两种解题思路．
思路1：将绕着点旋转，使得和重合，得到
思路2：延长到，使得，连接，根据可证得
根据上面任意一种解题思路，再结合三角形三边关系，我们都可以得到的取值范围为 ．
【类比探究】
如图②，，，，是的边上的中线，试探索与的数量关系，并说明理由．
【迁移应用】
【应用1】如图③，已知的半径为6，四边形是的圆内接四边形．，，求的长．
【应用2】如图④，，，，，，，、相交于点，连接，若的度数发生改变，请问是否存在最小值？如果存在，则直接写出其最小值（用含和的式子表示），如果不存在，请说明理由．
11．（2021•扬州模拟）我们定义：如图1，在中，把点绕点顺时针旋转得到，把绕点逆时针旋转得到，连接．我们称△是的“旋补交差三角形”，连接、，我们将、所在直线的相交而成的角称之为 “旋补交差角”， 点到中点间的距离成为“旋转中距”．如图1，即为 “旋补交差角”， 即为 “旋补中距”．
（1）若已知图1中的长度等于4，当，则 “旋补交差角” ，“旋补中距” 长度 ；
（2）若图1中的度数发生改变，则 “旋补交差角”度数是否发生改变？请证明你的结论，并直接判断 “旋补中距”是否也发生改变；
（3）已知图2中△是 “旋补交差三角形”， 的长度等于4，长度等于6，问是否存在最小值？如果存在，请求出具体的值，如果不存在，请说明理由．
12．（2021春•龙口市月考）如图，将置于直角坐标系中，，，点、分别在轴、轴上，且，．
（1）如图1，求点的坐标；
（2）如图2，、分别交轴、轴于、，请直接写出的值．
（3）如图3，为上一点，，且，为的中点，连接，，判断线段与的关系，并写出证明过程．
13．（2021秋•微山县期中）【发现问题】
小强在一次学习过程中遇到了下面的问题：
如图1，是的中线，若，，求的取值范围．
【探究方法】
小强所在学习小组探究发现：延长至点，使，连接．可证出，利用全等三角形的性质可将已知的边长与转化到同一个中，进而求出的取值范围．
方法小结：从上面思路可以看出，解决问题的关键是将中线延长一倍，构造出全等三角形，我们把这种方法叫做倍长中线法．
【应用方法】
（1）请你利用上面解答问题的方法思路，写出求的取值范围的过程；
【拓展应用】
（2）已知：如图2，是的中线，，点在的延长线上，．写出与之间的数量关系并证明．
14．（2021春•历下区期中）（1）方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在中，，，求边上的中线的取值范围．
小明在组内经过合作交流，得到了如下的解决方法（如图2），
①延长到，使得；
②连接，通过三角形全等把、、转化在中；
③利用三角形的三边关系可得的取值范围为，从而得到的取值范围是 ；
方法总结：上述方法我们称为“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系．
（2）请你写出图2中与的数量关系和位置关系，并加以证明．
（3）深入思考：如图3，是的中线，，，，请直接利用（2）的结论，试判断线段与的数量关系，并加以证明．
15．（2020•徐州模拟）（1）阅读理解：
如图①，在中，若，，求边上的中线的取值范围．
可以用如下方法：将绕着点逆时针旋转得到，在中，利用三角形三边的关系即可判断中线的取值范围是 ；
（2）问题解决：
如图②，在中，是边上的中点，于点，交于点，交于点，连接，求证：；
（3）问题拓展：
如图③，在四边形中，，，，以为顶点作一个的角，角的两边分别交、于、两点，连接，探索线段，，之间的数量关系，并说明理由．
16．（2020•建昌县模拟）如图，在和中，，，，绕点旋转．
（1）如图1，若连接，，则与的关系为 ；
（2）如图2，若连接，，取中点，连接，探究与的关系，并证明你的结论；
（3）在（2）的条件下，当旋转到如图3的位置时，点落在延长线上，若，，请直接写出线段的长．
17．（2020•德州）问题探究：
小红遇到这样一个问题：如图1，中，，，是中线，求的取值范围．她的做法是：延长到，使，连接，证明，经过推理和计算使问题得到解决．
请回答：（1）小红证明的判定定理是： ；
（2）的取值范围是 ；
方法运用：
（3）如图2，是的中线，在上取一点，连接并延长交于点，使，求证：．
（4）如图3，在矩形中，，在上取一点，以为斜边作，且，点是的中点，连接，，求证：．
18．（2019秋•鞍山期末）在利用构造全等三角形来解决的问题中，有一种典型的利用倍延中线的方法，例如：在中，，，点是边上的中点，怎样求的取值范围呢？我们可以延长到点，使，然后连接（如图①，这样，在和中，由于，，，接下来，在中通过的长可求出的取值范围．
请你回答：
（1）在图①中，中线的取值范围是 ．
（2）应用上述方法，解决下面问题
①如图②，在中，点是边上的中点，点是边上的一点，作交边于点，连接，若，，请直接写出的取值范围．
②如图③，在四边形中，，，点是中点，点在上，且满足，，连接、，请判断与的位置关系，并证明你的结论．
19．（2023春•皇姑区校级期中）已知等边和等腰，，．
（1）如图1，点在上，点在上，是的中点，连接，，则线段与之间的数量关系为 ；
（2）如图2，点在内部，点在外部，是的中点，连接、，则（1）中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由；
（3）如图3，若点在内部，点和点重合，点在下方，且，则的最大值为 ．
20．（2023•南关区校级二模）【提出问题】兴趣小组活动中老师提出了如下问题：如图①，在中，若，，求边上的中线的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长到，使得，，再连接（或将绕点逆时针旋转得到，把、、集中在中，利用三角形的三边关系可得，则．
【方法感悟】当条件中出现“中点”、“中线”等条件时，可以考虑作“辅助线”，把一条过中点的线段延长一倍，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中，这种作辅助线的方法称为“中线加倍”法．
【解决问题】如图②，在中，点是边的中点，点在边上，过点作，交边于点，连接．
（1）求证：．
（2）若，则线段、、之间的等量关系为 ．
（3）【应用拓展】如图③，在中，，点为边的中点，点和点分别在边、上，点为线段的中点．若，，则的长为 ．