浙江省金华市义乌市七校联考2023-2024学年八年级上学期12月月考数学试题

这是一份浙江省金华市义乌市七校联考2023-2024学年八年级上学期12月月考数学试题，共11页。试卷主要包含了已知等内容，欢迎下载使用。

考生须知：
1．试卷共有三大题，24小题，全卷满分为120分。
2．答案必须做在相应的答题卷位置上，做在试题卷上无效。
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！祝你成功！
一、选择题（共10小题，每题3分，共30分。）
1．（3分）下列历届亚运会会徽中是轴对称图形的是（ ）
A． B． C． D．
2．（3分）若，则下列式子中正确的是（ ）
A． B． C． D．
3．（3分）对于命题“如果，那么”，能说明它是假命题的反例是（ ）
A． B．
C． D．
4．（3分）如图，有一块三角形玻璃，小明不小心将它打破．带上这块玻璃，能配成同样大小的一块，其理由是（ ）
A． B． C． D．
5．（3分）一次函数的图象与x轴的交点坐标是（ ）．
A． B． C． D．
6．（3分）将一副直角三角板ABC和EDF如图放置（其中），使点E落在AC边上，且，则的度数为（ ）
A． B． C． D．
7．（3分）如图是画在方格纸上的某地部分旅游景点简图，建立直角坐标系后，狮子岩、永嘉书院与埭头古村的坐标分别是，下列地点中离原点最近的是（ ）
A．狮子岩 B．龙瀑仙洞 C．埭头古村 D．永嘉书院
8．（3分）某业主贷款9万元购进一台机器生产甲，乙两种产品、已知甲产品的销售净利润是每个5元，乙产品的销售净利润是每个6元，2个甲产品和1个乙产品组成一套销售，设销售x套能赚回这台机器的贷款，则x满足的关系是（ ）
A． B．
C． D．
9．（3分）已知：纸片，将纸片分别按以下两种方法翻折：
①如图1，沿着的平分线AD翻折，得到，设的周长为m．
②如图2，沿着AB的垂直平分线翻折，得到，设的周长为n．
线段AB的长度用含m，n的代数式可表示为（ ）
图1 图2
A． B． C．m D．
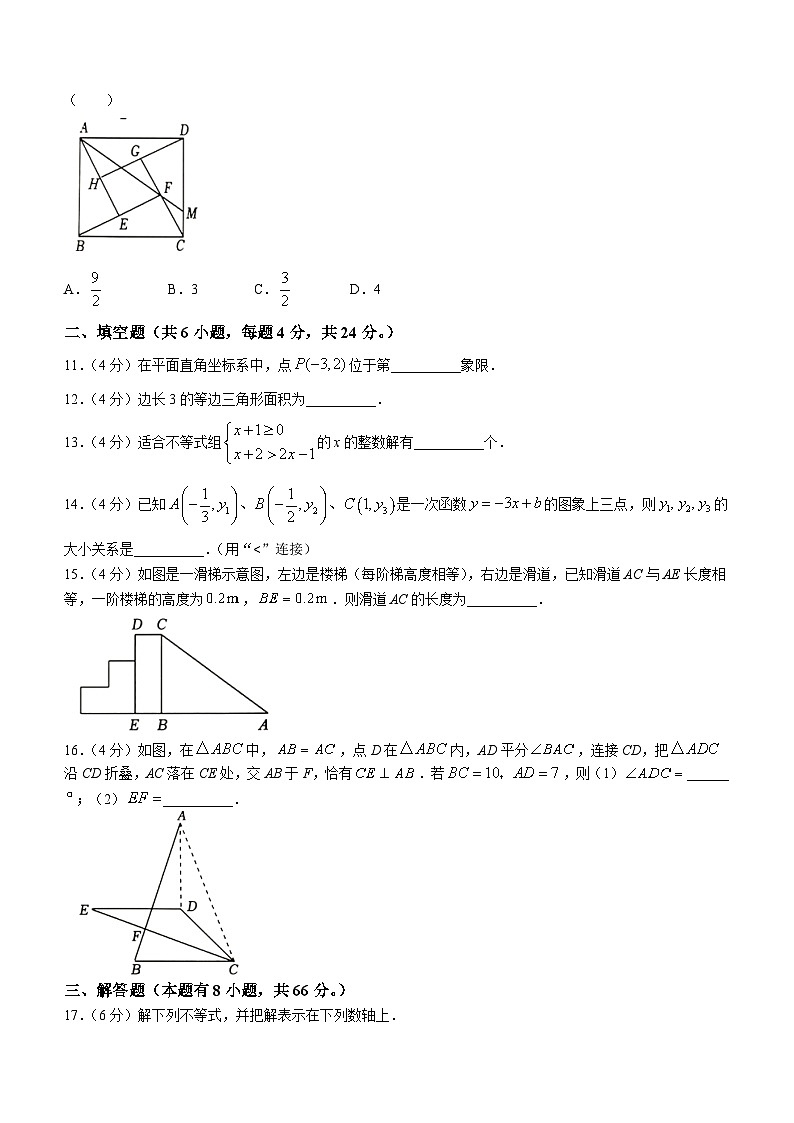
10．（3分）赵爽是我国汉代数学家，大约在公元222年，他为《周髀算经》作注解时，给出了“赵爽弦图：四个全等的直角三角形与一个小正方形拼成一个大的正方形．如图，边长为6的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，连结AF并延长交CD于点M．若，则DM的长是（ ）
A． B．3 C． D．4
二、填空题（共6小题，每题4分，共24分。）
11．（4分）在平面直角坐标系中，点位于第__________象限．
12．（4分）边长3的等边三角形面积为__________．
13．（4分）适合不等式组的x的整数解有__________个．
14．（4分）已知是一次函数的图象上三点，则的大小关系是__________．（用“<”连接）
15．（4分）如图是一滑梯示意图，左边是楼梯（每阶梯高度相等），右边是滑道，已知滑道AC与AE长度相等，一阶楼梯的高度为，．则滑道AC的长度为__________．
16．（4分）如图，在中，，点D在内，AD平分，连接CD，把沿CD折叠，AC落在CE处，交AB于F，恰有．若，则（1）______；（2）__________．
三、解答题（本题有8小题，共66分。）
17．（6分）解下列不等式，并把解表示在下列数轴上．
18．（6分）如图，在和中，点A、D、B、E在同一直线上，，．
（1）求证：；
（2）当时，求的度数．
19．（6分）如图，（1）在的正方形网格中建立平面直角坐标系，使点A的坐标为，点B的坐标为．
（2）将点A向下平移5个单位，再关于y轴对称得到点C，求点C坐标；
（3）画出三角形ABC，并求其面积．
20．（8分）在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B．
（1）直接写出点A，B的坐标：A：__________；B：__________．
（2）如图，将直线绕点B逆时针旋转，得到直线，求直线的表达式．
小明想利用“一线三等角”模型解决这个问题．如图，过点A作AB的垂线交于点C，可求出点C的坐标为__________，从而求得直线的表达式为__________．
21．（8分）如图，在中，，分别交BC、AC于点D、E，点F在BC的延长线上，且．
（1）求证：是等腰三角形；
（2）连接AD，当，的周长为16时，求的周长．
22．（10分）污水治理，保护环境，某市治污公司决定购买A，B两种型号污水处理设备共12台，已知A，B两种型号的设备，每台的价格，月处理污水量如表：
经调查：购买一台A型设备比购买一台B型设备多3万元，购买1台A型设备比购买3台B型设备少3万元．
（1）求a，b的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过50万元，你认为该公司有哪几种购买方案；
（3）在（2）问的条件下，若每月要求处理的污水量不低于2260吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案，
23．（10分）一次函数b（k，b是常数，）和的图象交于点A．
（1）若点A在x轴上，求的值．
（2）若点，当时，，直接写出k的取值范围．
（3）若，点在一次函数图象上，求证：．
24．（12分）根据以下素材，探索完成任务
八年级数学第十六周校本作业参考答案
选择题
填空题
11．二 12． 13．4 14． 15．1 16．135
17．（6分）解下列不等式，并把解表示在下列数轴上．
．
解： 4分
图略 2分
18．（6分）
（1）
即 1分
又 2分
（2） 3分
19．（6分）（1）如图 2分
（2）点A向下平移5个单位得到点，关于y轴对称的点； 2分
（3）（割补均可）． 2分
20．（8分）
（1）点A，B的坐标： 1分+1分
（2）点C的坐标， 3分
直线的表达式为 3分
21．（8分）（1）证明：中，
，
，
，
，
，
，
，
是等腰三角形； 4分
（2）连接AD，当时，
，
，
周长，
，
的周长周长． 4分
22．（10分）解：（1）根据题意得：，
解得：． 3分
（2）设购买污水处理设备A型设备x台，B型设备台，根据题意得，
，
，
取正整数，
，
，
有四种购买方案：
①A型设备1台，B型设备11台；
②A型设备2台，B型设备10台；
③A型设备3台，B型设备9台；
④A型设备4台，B型设备8台． 4分
（3）由题意：，
，
又，
，
取正整数，
为3，4．
当时，购买资金为（万元），
当时，购买资金为（万元），
，
为了节约资金，应选购A型设备3台，B型设备9台． 3分
23．（10分）（1）解：在x轴上，
设，代入，解得，
将代入，得：，
整理，得：． 3分
（2）解：将代入，得：，
将，画图分析高低情况可知． 3分
（3）证明：将代入，得：，
，解得：，
，
． 4分
24．（12分）任务一：
证明：，
，
在和中，
，
，
是的角平分线； 4分
任务二
解：，
，
，
，
过点E作于点G，如图，
在中，
，
，
在中，
由勾股定理，得，
，
4分
答：当伞从完全张开到完全收拢，伞圈D移动的距离为
任务三：60 4分A型
B型
价格（万元/台）
a
b
处理污水量（吨/月）
220
180
探究纸伞中的数学问题
素材1
我国纸伞制作工艺十分巧妙，如图1，伞不管是张开还是收拢，AP是伞柄，伞骨，且，，D点为伞圈，．
图1
素材2
伞圈D能沿着伞柄滑动，如图2是完全收拢时伞骨的示意图，此时伞圈D滑动到的位置，且A、E、三点共线，测得，，伞完全张开时，如图1所示．（参考值：）
图2
素材3
项目化学习小组同学经过研究发现：雨往往是斜打的，且都是平行的．如图3，某一天，雨线BM与地面夹角为小明同学站在伞圈D点的正下方G处，记为GH，此时，发现身上被雨淋湿，测得．
图3
问题解决
任务1
判断AP位置
求证：AP是的角平分线．
任务2
探究伞圈移动距离
当伞从完全张开到完全收拢，求伞圈D移动的距离．
任务3
拟定撑伞方案
求伞至少向下移动距离__________，使得人站在G处身上不被雨淋湿，（直接写出答案）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
B
C
C
B
A
D
A