2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.3 利用递推公式求通项（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.3 利用递推公式求通项（精讲）（提升版）（原卷版+解析版），共26页。试卷主要包含了累加法，累乘法，公式法，构造等差数列，构造等比数列等内容，欢迎下载使用。


考点呈现
例题剖析
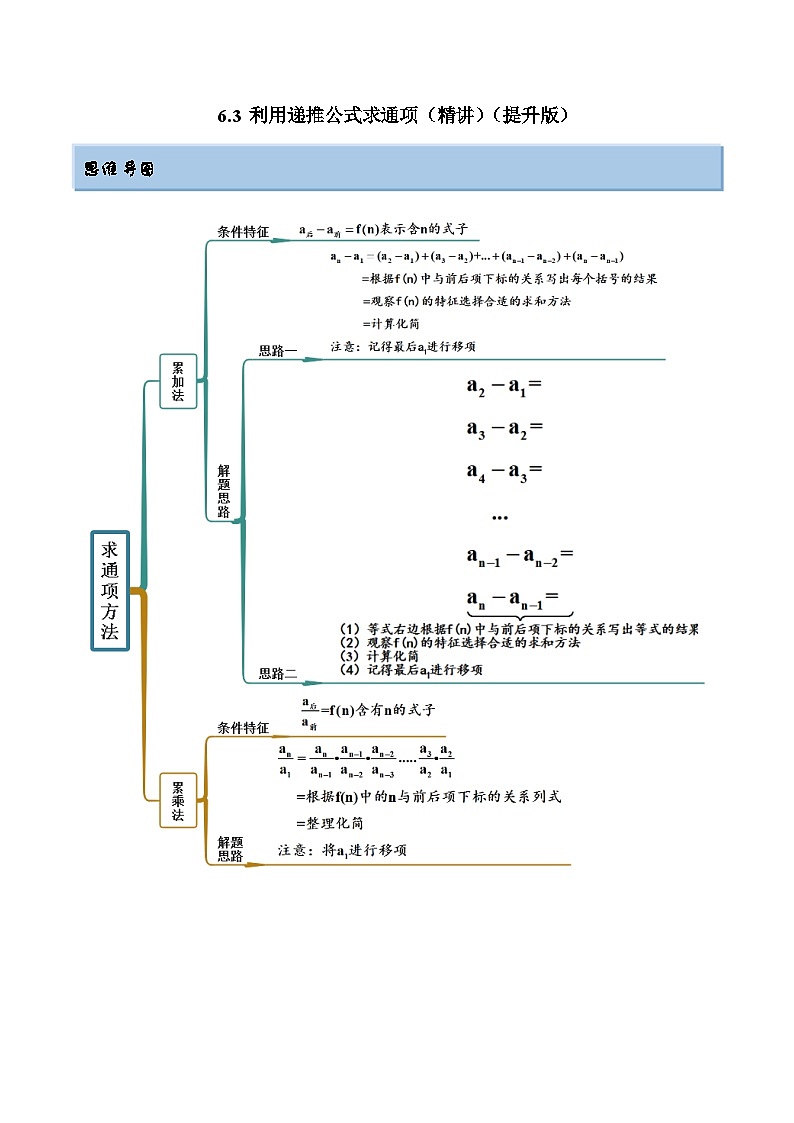
考点一 累加法
【例1-1】 (2023·河南·灵宝市）已知数列满足，且,求数列的通项公式；
．
【例1-2】 (2023·江苏江苏·一模）已知数列，，且，，求数列的通项公式
【一隅三反】
1． (2023.广东）数列满足，，则= 。
2． (2023.广东）在数列{an}中，若a1＝﹣2，an+1＝an+n•2n，则an＝ 。
3．已知数列中，，，则数列的一个通项公式为 。
考点二 累乘法
【例2】 (2023·全国·模拟预测（理））已知数列满足．求数列的通项公式；
【一隅三反】
1. (2023·安徽安庆）已知数列的前n项和为，且满足，.求的通项公式；
2．（2022·全国·专题练习）设是首项为1的正项数列且，求数列的通项公式 .
4． (2023·全国·专题练习）设是首项为1的正项数列，且 ，求通项公式.=
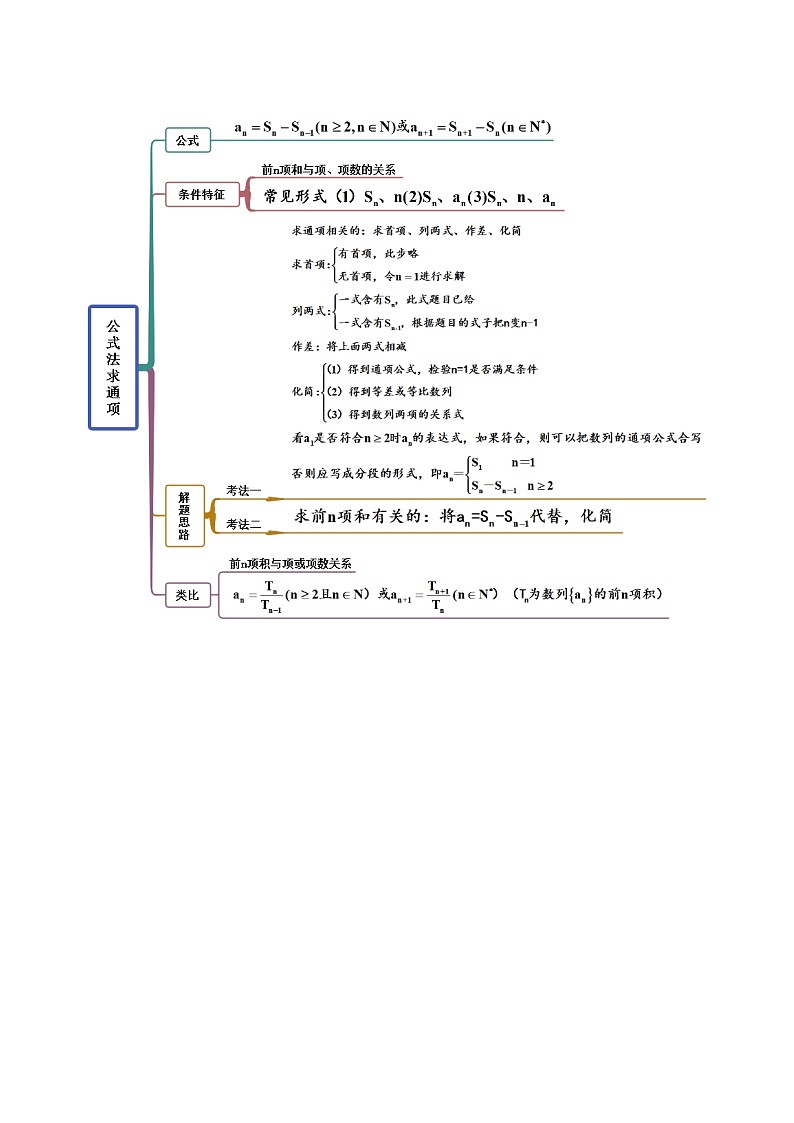
考点三 公式法
【例3-1】 (2023·四川）数列的前项和，则它的通项公式是_______．
【例3-2】 (2023·安徽宿州）已知数列的前n项和为，且，则的通项公式为______．
【例3-3】． (2023·北京交通大学附属中学）已知数列满足，则____.
【例3-4】． (2023·山西太原·二模（文））已知数列的首项为1，前n项和为，且，则数列的通项公式___________.
【一隅三反】
1． (2023·湖北）数列中，已知，且（且），则此数列的通项公式为__________.
2．（2022·全国·专题练习）（多选）在数列中，其前的和是 ，下面正确的是（ ）
A．若 ，则其通项公式
B．若，则其通项公式
C．若，则其通项公式
D．若，，则其通项公式
3． (2023·全国·高三专题练习）（多选）在数列中，其前的和是，下面正确的是（ ）
A．若，，则
B．若 ，则
C．若 ，则
D．若 ，且，则
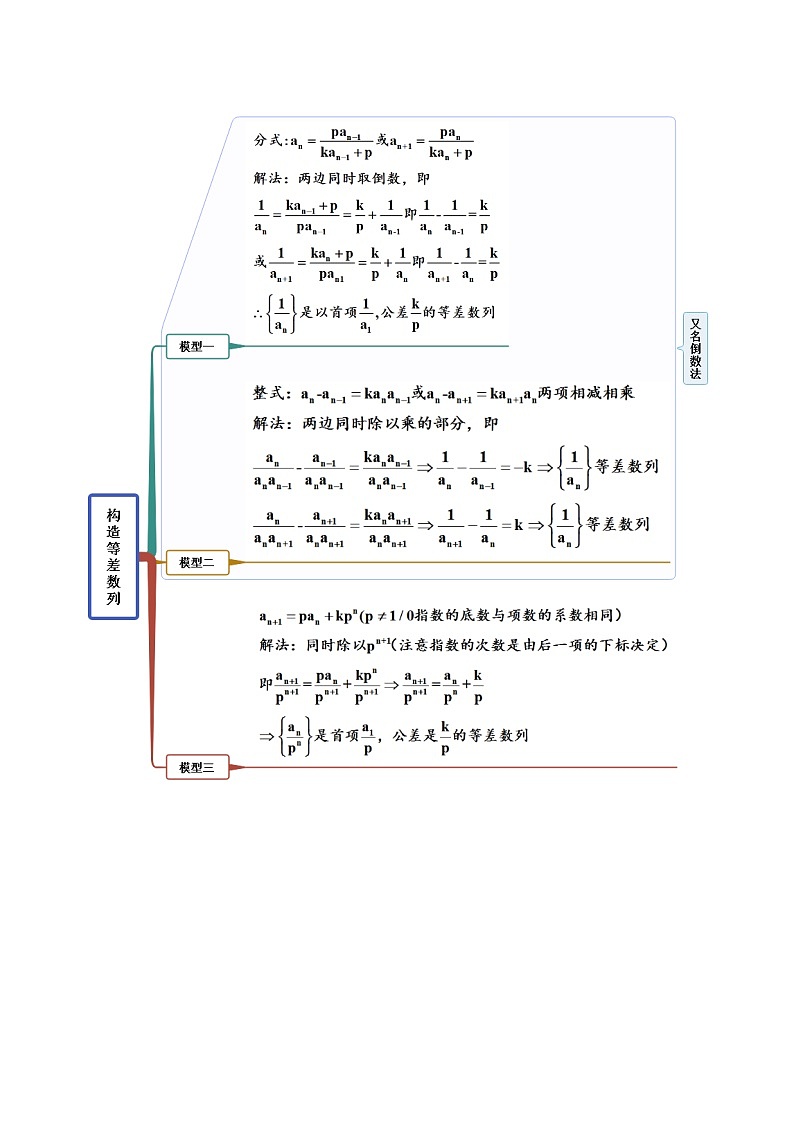
考点四 构造等差数列
【例4-1】 (2023·四川省绵阳南山中学）已知数列满足，，，则满足的n的最大取值为（ ）
A．7B．8C．9D．10
【例4-2】 (2023·广东肇庆·二模）已知是数列的前n项和，，，恒成立，则k最小为______．
【例4-3】 (2023·江西）已知数列满足：，（，），则___________.
【一隅三反】
1． (2023·全国·高三专题练习）已知数列满足，且，则的通项公式_______________________.
2． (2023·全国·高三专题练习）已知数列满足，且，则数列的通项公式______．
3． (2023·全国·课时练习）已知数列中，，求数列的通项公式；
4． (2023·全国·高三专题练习）已知数列中，，．求数列的通项公式；
5． (2023·全国·高三专题练习）已知数列中，，，求数列的通项公式.
考点五 构造等比数列
【例5-1】 (2023·全国·高三专题练习）已知，，则________．
【例5-2】 (2023·全国·高三专题练习）已知在数列中，，，则（ ）
A．B．C．D．
【例5-3】 (2023·全国·课时练习）已知数列满足，．数列满足，则数列的通项公式为________．
【一隅三反】
1． (2023·福建省）已知数列满足，，则的前n项和为___.
2．（2022·山西师范大学实验中学）已知数列满足，，则___________.
3． (2023·全国·高三专题练习）若正项数列满足，则数列的通项公式是_______．
4． (2023·黑龙江·龙江县第一中学）已知数列的通项公式为，求数列的通项公式.
6.3 利用递推公式求通项（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 累加法
【例1-1】 (2023·河南·灵宝市）已知数列满足，且,求数列的通项公式；
【答案】
【解析】因为，所以，
，…，所以．
又，所以，所以．又，也符合上式，所以．
【例1-2】 (2023·江苏江苏·一模）已知数列，，且，，求数列的通项公式
【答案】
【解析】因为，所有，
当时，，，……，，
相加得，所以，当时，也符合上式，所以数列的通项公式
【一隅三反】
1． (2023.广东）数列满足，，则= 。
【答案】
【解析】，，则当时，，
。
2． (2023.广东）在数列{an}中，若a1＝﹣2，an+1＝an+n•2n，则an＝ 。
【答案】（n﹣2）•2n
【解析】∵an+1＝an+n•2n，∴an+1﹣an＝n•2n，且a1＝﹣2
∴an﹣a1＝an﹣an﹣1+an﹣1﹣an﹣2+…+a2﹣a1＝（n﹣1）•2n﹣1+…+2•22+1•21，①
∴2（an﹣a1）＝（n﹣1）•2n+（n﹣2）•2n﹣1+…+2•23+1•22，②
①-①得﹣（an﹣a1）＝﹣（n﹣1）•2n+2n﹣1+2n﹣2+…+23+22+2
＝﹣（n﹣1）•2n+﹣（n﹣1）•2n﹣2+2n，
∴an﹣a1＝（n﹣1）•2n+2﹣2n，所以an＝（n﹣2）•2n
3．已知数列中，，，则数列的一个通项公式为 。
【答案】
【解析】因为则
由递推公式可得

将等式两边分别相加可得
所以由对数运算可得
考点二 累乘法
【例2】 (2023·全国·模拟预测（理））已知数列满足．求数列的通项公式；
【答案】；
【解析】当时，，则，即，
，n＝1也满足上式，故；
【一隅三反】
1. (2023·安徽安庆）已知数列的前n项和为，且满足，.求的通项公式；
【答案】，
【解析】时，，解得.
当时，，故，所以，
故.
符合上式故的通项公式为，.
2．（2022·全国·专题练习）设是首项为1的正项数列且，求数列的通项公式 .
【答案】或
【解析】依题意，
所以，
当时，，所以.
当时，，
所以
，
也符合上式.
所以.
综上所述，或.
4． (2023·全国·专题练习）设是首项为1的正项数列，且 ，求通项公式.=
【答案】
【解析】由，得，
∵，∴，∴ ，∴，
∴，
又a1＝1满足上式，∴.
考点三 公式法
【例3-1】 (2023·四川）数列的前项和，则它的通项公式是_______．
【答案】
【解析】当时，，
当时，
经检验当时不符合，所以，故答案为：
【例3-2】 (2023·安徽宿州）已知数列的前n项和为，且，则的通项公式为______．
【答案】
【解析】当时，，得，
当时，由，得，所以，所以，所以，
所以数列是以1为首项，为公比的等比数列，所以，故答案为：
【例3-3】． (2023·北京交通大学附属中学）已知数列满足，则____.
【答案】
【解析】因为，所以当时，有，
，得，当时，也适合，故答案为：
【例3-4】． (2023·山西太原·二模（文））已知数列的首项为1，前n项和为，且，则数列的通项公式___________.
【答案】n
【解析】∵，∴
当时，，
当时，成立，∴，
当时，，
当时，满足上式，∴.故答案为：n
【一隅三反】
1． (2023·湖北）数列中，已知，且（且），则此数列的通项公式为__________.
【答案】
【解析】由得：
（且）
（且）即（且）
数列是第二项起公比为的等比数列，
（且）又不满足上式，
2．（2022·全国·专题练习）（多选）在数列中，其前的和是 ，下面正确的是（ ）
A．若 ，则其通项公式
B．若，则其通项公式
C．若，则其通项公式
D．若，，则其通项公式
【答案】BCD
【解析】A：时，，当时，，而，故错误；
B：由题设，，，，，…，则，故正确；
C：由题设，，而，则，即，故正确；
D：假设成立，当时，，即成立；
若时，成立，则时，，
此时，则也成立，故正确.
故选：BCD
3． (2023·全国·高三专题练习）（多选）在数列中，其前的和是，下面正确的是（ ）
A．若，，则
B．若 ，则
C．若 ，则
D．若 ，且，则
【答案】ABC
【解析】A：由题设，是首项为1，公差为2的等差数列，则，正确；
B：由题设，，则，可得，即，正确；
C：由题设，，则，正确；
D：时有，整理得，而，故为常数列且，可得，错误；故选：ABC
考点四 构造等差数列
【例4-1】 (2023·四川省绵阳南山中学）已知数列满足，，，则满足的n的最大取值为（ ）
A．7B．8C．9D．10
【答案】C
【解析】解：因为，所以，所以，又，
数列是以1为首项，4为公差的等差数列．
所以，所以，由，即，即，解得，因为为正整数，所以的最大值为；
故选：C
【例4-2】 (2023·广东肇庆·二模）已知是数列的前n项和，，，恒成立，则k最小为______．
【答案】2
【解析】由，得，
当时，得，，…，，
则，
即，则，
当n=1时符合上式，
则，
所以k最小为2．
故答案为：.
【例4-3】 (2023·江西）已知数列满足：，（，），则___________.
【答案】
【解析】由题设，，即，而，
∴是首项、公差均为的等差数列，即，
∴.故答案为：
【一隅三反】
1． (2023·全国·高三专题练习）已知数列满足，且，则的通项公式_______________________.
【答案】
【解析】由,得，则，
由得，所以是以为首项，为公差的等差数列，
所以，
当时，，
所以，当时，也适合上式，所以，故答案为：.
2． (2023·全国·高三专题练习）已知数列满足，且，则数列的通项公式______．
【答案】
【解析】∵，
∴，
即．又，，
∴数列是以3为首项，1为公差的等差数列，
∴，
∴数列的通项公式．
故答案为：.
3． (2023·全国·课时练习）已知数列中，，求数列的通项公式；
【答案】．
【解析】由，得：，∴，
即数列是首项为1，公差为2的等差数列，∴，得．
4． (2023·全国·高三专题练习）已知数列中，，．求数列的通项公式；
【答案】
【解析】因为，所以令，则，解得，
对两边同时除以，得，
又因为，所以是首项为1，公差为2的等差数列，
所以，所以；
5． (2023·全国·高三专题练习）已知数列中，，，求数列的通项公式.
【答案】
【解析】∵，∴，∴数列是等差数列，公差为，又，
∴，∴.
考点五 构造等比数列
【例5-1】 (2023·全国·高三专题练习）已知，，则________．
【答案】
【解析】将变形为,所以数列是首项为2,公比为2的等比数列,所以,即公比为2的等比数列,所以,即.故答案为：
【例5-2】 (2023·全国·高三专题练习）已知在数列中，，，则（ ）
A．B．C．D．
【答案】A
【解析】因为，，所以，整理得，所以数列是以为首项，为公比的等比数列．所以，解得．
故选：A
【例5-3】 (2023·全国·课时练习）已知数列满足，．数列满足，则数列的通项公式为________．
【答案】
【解析】∵，∴，即,∴,
且，，则,又，
∴数列是首项为，公比为3的等比数列．∴．故答案为：.
【一隅三反】
1． (2023·福建省）已知数列满足，，则的前n项和为___.
【答案】
【解析】数列满足，整理得：，所以，
又，故是以4为首项，2为公比的等比数列，
所以，所以，所以的前项和
故答案为：
2．（2022·山西师范大学实验中学）已知数列满足，，则___________.
【答案】
【解析】由已知可得，设，则，
所以，，可得，所以，，且，
由题意可知，对任意的，，则，
所以，数列为等比数列，且该数列的首项为，公比为，
所以，，因此，.
故答案为：.
3． (2023·全国·高三专题练习）若正项数列满足，则数列的通项公式是_______．
【答案】
【解析】在正项数列中，，则有，
于是得，而，因此得：数列是公比为2的等比数列，
则有，即，
所以数列的通项公式是.
故答案为：
4． (2023·黑龙江·龙江县第一中学）已知数列的通项公式为，求数列的通项公式.
【答案】
【解析】因为，所以，则，
又，所以数列是以为首项，为公比的等比数列，
所以，所以，所以；