2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.2 古典概型及条件概率（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.2 古典概型及条件概率（精讲）（基础版）（原卷版+解析版），共20页。试卷主要包含了古典概型，条件概率，综合运用等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 古典概型
【例1】 (2023·河南安阳）某市在疫情期间，便民社区成立了由网格员､医疗人员､志愿者组成的采样组，并上门进行，核酸检测，某网格员对该社区需要上门核酸检测服务的老年人的年龄（单位：岁）进行了统计调查，将得到的数据进行适当分组后（每组为左开右闭区间），得到的频率分布直方图如图所示.
(1)求m的值，并估计需要上门核酸检测服务的老年人的年龄的平均数；（精确到1，同一组中的数据用该组区间的中点值作为代表）
(2)在年龄处于的老人中，用分层随机抽样的方法选取9人，再从9人中随机选取2人，求2人中恰有1人年龄超过需要上门核酸检测服务的老年人的平均年龄的概率.
【一隅三反】
1．（2022河北省）某校为了保障体艺节顺利举办，从高一、高二两个年级的同学中挑选了志愿者60人，人数如下表所示：
(1)从所有志愿者中任意抽取一人，求抽到的这人是女同学的概率；
(2)用等比例分层随机抽样的方法从所有的女志愿者中按年级抽取六人，再从这六人中随机抽取两人接受记者采访，求这两人中恰有一人来自高一年级的概率.
2． (2023·广东）新冠肺炎疫情期间，某地为了了解本地居民对当地防疫工作的满意度，从本地居民中随机抽取若干居民进行评分（满分为分），根据调查数据制成如下频率分布直方图，已知评分在的居民有人．
(1)求频率分布直方图中的值；
(2)根据频率分布直方图估计本次评测分数的平均数（同一组中的数据用该组区间的中点值作代表，并精确到）；
(3)为了今后更好地完成当地的防疫工作，政府部门又采用比例分配的分层抽样的方法，从评分在的居民中选出人进行详细的调查，再从中选取两人进行面对面沟通，求选出的两人恰好都是评分在之间的概率．
3． (2023·四川眉山）某校高二（2）班的一次化学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图：
(1)求全班人数及全班分数的中位数；
(2)根据频率分布直方图估计该班本次测试的平均成绩（同一组中的数据用该组区间的中点值为代表）.
(3)若从分数在及的答题卡中采用分层抽样的方式抽取了5份答题卡，再从抽取的这5份答题卡中随机抽取2份答题卡了解学生失分情况，求这2份答题卡至少有一份分数在的概率.
考点二 条件概率
【例2-1】 (2023·广东·石门高级中学高二阶段练习）设，则（ ）
A．B．C．D．
【例2-2】 (2023·陕西渭南·高二期末（文））甲、乙两人到一商店购买饮料，他们准备分别从加多宝、唯怡豆奶、雪碧这3种饮品中随机选择一个，且两人的选择结果互不影响．记事件“甲选择唯怡豆奶”，事件“甲和乙选择的饮品不同”，则条件概率________．
【例2-3】 (2023·广东·石门高级中学高二阶段练习）已知箱中有5个大小相同的产品，其中3个正品，2个次品，每次从箱中取1个，不放回的取两次，求：
(1)第一次取到正品的概率；
(2)在第一次取到正品的条件下，第二次取到正品的概率.
【一隅三反】
1． (2023·福建）设A，B为两个事件，已知，，，则（ ）
A．0.24B．0.375C．0.4D．0.5
2． (2023·陕西西安）长时间玩手机可能影响视力，据调查，某校学生大约的人近视，而该校大约有的学生每天玩手机超过，这些人的近视率约为．现从该校近视的学生中任意调查一名学生，则他每天玩手机超过的概率为（ ）
A．B．C．D．
3． (2023·福建三明）有3箱同一品种的零件，每箱装有10个零件，其中第一箱内一等品6个，第二箱内一等品4个，第三箱内一等品2个，现从3箱中随机挑出一箱，然后从该箱中依次随机取出2个，取出的零件均不放回，求：
(1)第1次取出的零件是一等品的概率；
(2)在第1次取出的零件是一等品的条件下，第2次取出的零件也是一等品的概率．
考点三 综合运用
【例3】 (2023·江苏扬州·高三期末）为了更好满足人民群众的健身和健康需求，国务院印发了《全民健身计划（）》．某中学为了解学生对上述相关知识的了解程度，先对所有学生进行了问卷测评，所得分数的分组区间为、、、、，由此得到总体的频率分布直方图，再利用分层抽样的方式随机抽取名学生进行进一步调研，已知频率分布直方图中、、成公比为的等比数列．
(1)若从得分在分以上的样本中随机选取人，用表示得分高于分的人数，求的分布列及期望；
(2)若学校打算从这名学生中依次抽取名学生进行调查分析，求在第一次抽出名学生分数在区间内的条件下，后两次抽出的名学生分数在同一分组区间的概率．
【一隅三反】
1． (2023·全国·高三专题练习）某校从学生文艺部6名成员（4男2女）中，挑选2人参加学校举办的文艺汇演活动.
（1）求男生甲被选中的概率；
（2）在已知男生甲被选中的条件下，女生乙被选中的概率.
2． (2023·辽宁沈阳·二模）甲、乙是北京2022冬奥会单板滑雪坡面障碍技巧项目的参赛选手，二人在练习赛中均需要挑战3次某高难度动作，每次挑战的结果只有成功和失败两种．
(1)甲在每次挑战中，成功的概率都为．设X为甲在3次挑战中成功的次数，求X的分布列和数学期望；
(2)乙在第一次挑战时，成功的概率为0.5，受心理因素影响，从第二次开始，每次成功的概率会发生改变其规律为：若前一次成功，则该次成功的概率比前一次成功的概率增加0.1；若前一次失败，则该次成功的概率比前一次成功的概率减少0.1．
（ⅰ）求乙在前两次挑战中，恰好成功一次的概率；
（ⅱ）求乙在第二次成功的条件下，第三次成功的概率．高一年级
高二年级
男同学
女同学
男同学
女同学
16
12
8
24
6.2 古典概型及条件概率（精讲）（基础版）
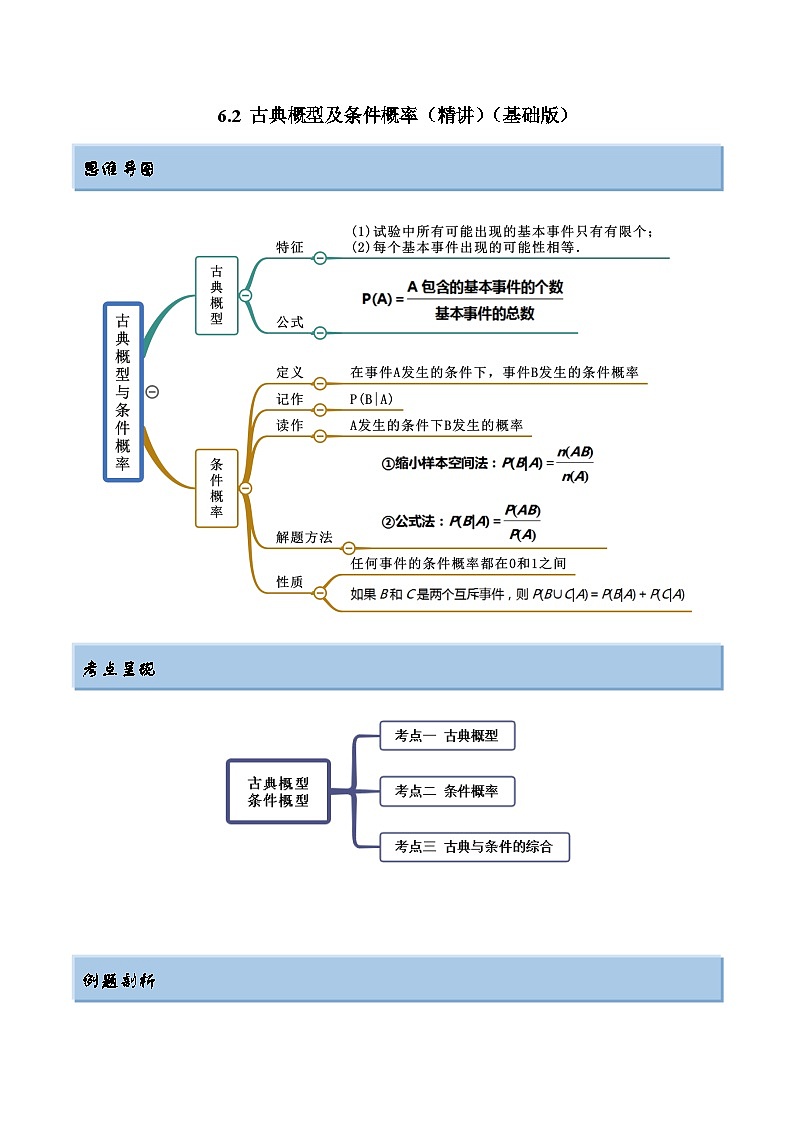
思维导图
考点呈现
例题剖析
考点一 古典概型
【例1】 (2023·河南安阳）某市在疫情期间，便民社区成立了由网格员､医疗人员､志愿者组成的采样组，并上门进行，核酸检测，某网格员对该社区需要上门核酸检测服务的老年人的年龄（单位：岁）进行了统计调查，将得到的数据进行适当分组后（每组为左开右闭区间），得到的频率分布直方图如图所示.
(1)求m的值，并估计需要上门核酸检测服务的老年人的年龄的平均数；（精确到1，同一组中的数据用该组区间的中点值作为代表）
(2)在年龄处于的老人中，用分层随机抽样的方法选取9人，再从9人中随机选取2人，求2人中恰有1人年龄超过需要上门核酸检测服务的老年人的平均年龄的概率.
【答案】(1)，平均数为岁(2)
【解析】（1）解：由图可得，解得.估计需要上门核酸检测服务的老年人的年龄的平均数为岁.
（2）解：，两组的人数之比为，∴在，的老人中抽取的人数分别为4，5，分别记为，，，，，，，，，从9人中随机选取2人，样本空间，共有36个样本点，恰有一人年龄超过80岁，即恰有一人年龄在，令“恰有一人年龄在”为事件B，则，共有20个样本点，∴.
【一隅三反】
1．（2022河北省）某校为了保障体艺节顺利举办，从高一、高二两个年级的同学中挑选了志愿者60人，人数如下表所示：
(1)从所有志愿者中任意抽取一人，求抽到的这人是女同学的概率；
(2)用等比例分层随机抽样的方法从所有的女志愿者中按年级抽取六人，再从这六人中随机抽取两人接受记者采访，求这两人中恰有一人来自高一年级的概率.
【答案】(1)(2)
【解析】（1）高一年级志愿者有人，其中女同学12人，高二年级志愿者有人，其中女同学24人.故抽到的这人是女同学的概率.
（2）在高一年级中抽取的志愿者的人数为2，在高二年级中抽取的志愿者的人数为4.记从高一年级中抽取的志愿者为a，b，从高二年级中抽取的志愿者为A，B，C，D，样本空间，共15个样本点.设事件“这两人中恰有一人来自高一年级”，则，共8个样本点.故所求概率为.
2． (2023·广东）新冠肺炎疫情期间，某地为了了解本地居民对当地防疫工作的满意度，从本地居民中随机抽取若干居民进行评分（满分为分），根据调查数据制成如下频率分布直方图，已知评分在的居民有人．
(1)求频率分布直方图中的值；
(2)根据频率分布直方图估计本次评测分数的平均数（同一组中的数据用该组区间的中点值作代表，并精确到）；
(3)为了今后更好地完成当地的防疫工作，政府部门又采用比例分配的分层抽样的方法，从评分在的居民中选出人进行详细的调查，再从中选取两人进行面对面沟通，求选出的两人恰好都是评分在之间的概率．
【答案】(1)(2)(3)
【解析】（1），.
（2）平均数为.
（3）评分在和的频率之比为，应在评分在的居民中应抽取人，记为；在的居民中应抽取人，记为，则从中选取两人有，，，，，，，，，，，，，，，共种情况；其中选出的两人恰好都是评分在之间的有，仅有种；所求概率.
3． (2023·四川眉山）某校高二（2）班的一次化学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图：
(1)求全班人数及全班分数的中位数；
(2)根据频率分布直方图估计该班本次测试的平均成绩（同一组中的数据用该组区间的中点值为代表）.
(3)若从分数在及的答题卡中采用分层抽样的方式抽取了5份答题卡，再从抽取的这5份答题卡中随机抽取2份答题卡了解学生失分情况，求这2份答题卡至少有一份分数在的概率.
【答案】(1)人，分(2)(3)
【解析】（1）解：由茎叶图可知，分数在内的频数为3，由频率分布直方图可知，分数在内的频率为，所以， 全班人数为人，因为分数在内的频数为11，分数在内的频数为16，所以，全班分数的中位数.
（2）解：由茎叶图知，分数在内的频数为3，在内的频数为11，分数在内的频数为16，在内的频数为8，所以，分数在内的频数为，所以，该班本次测试的平均成绩为.
（3）解：因为分数在内的频数为，在内的频数为8，所以，由分层抽样抽取了5份答题卡中，分数在内的有份，分别记为，分数在内的有份，分别记为，所以，从抽取的这5份答题卡中随机抽取2份答题卡的所有情况有：，，，共10种，其中，这2份答题卡至少有一份分数在内的情况有：，，，共7种，所以，这2份答题卡至少有一份分数在的概率为.
考点二 条件概率
【例2-1】 (2023·广东·石门高级中学高二阶段练习）设，则（ ）
A．B．C．D．
【答案】D
【解析】因为，且，所以
，所以，故选：D.
【例2-2】 (2023·陕西渭南·高二期末（文））甲、乙两人到一商店购买饮料，他们准备分别从加多宝、唯怡豆奶、雪碧这3种饮品中随机选择一个，且两人的选择结果互不影响．记事件“甲选择唯怡豆奶”，事件“甲和乙选择的饮品不同”，则条件概率________．
【答案】
【解析】由题意得，设加多宝、唯怡豆奶、雪碧分别标号为，则两人的选择结果有：
,，则事件的可能结果为：共3个，
在事件的条件下发生事件的结果有，共2个，所以.故答案为: .
【例2-3】 (2023·广东·石门高级中学高二阶段练习）已知箱中有5个大小相同的产品，其中3个正品，2个次品，每次从箱中取1个，不放回的取两次，求：
(1)第一次取到正品的概率；
(2)在第一次取到正品的条件下，第二次取到正品的概率.
【答案】(1)(2)
【解析】（1）解：设“第一次取到正品” “第二次取到正品”，所以，第一次取到正品的概率为；
（2）解：，所以，故在第一次取到正品的条件下第二次取到正品的概率为.
【一隅三反】
1． (2023·福建）设A，B为两个事件，已知，，，则（ ）
A．0.24B．0.375C．0.4D．0.5
【答案】B
【解析】由，，得，所以.故选：B
2． (2023·陕西西安）长时间玩手机可能影响视力，据调查，某校学生大约的人近视，而该校大约有的学生每天玩手机超过，这些人的近视率约为．现从该校近视的学生中任意调查一名学生，则他每天玩手机超过的概率为（ ）
A．B．C．D．
【答案】A
【解析】从该校学生中任意调查一名学生他是近视记为事件A，且，从该校学生中任意调查一名学生他每天玩手机超过记为事件B，且由题可知，，所以从该校近视的学生中任意调查一名学生，则他每天玩手机超过的概率为：.故B，C，D错误.故选：A.
3． (2023·福建三明）有3箱同一品种的零件，每箱装有10个零件，其中第一箱内一等品6个，第二箱内一等品4个，第三箱内一等品2个，现从3箱中随机挑出一箱，然后从该箱中依次随机取出2个，取出的零件均不放回，求：
(1)第1次取出的零件是一等品的概率；
(2)在第1次取出的零件是一等品的条件下，第2次取出的零件也是一等品的概率．
【答案】(1)(2)
【解析】(1)设＝“被挑出的是第i箱”，＝“第i次取出的零件是一等品”，
则， 因为，，
所以第1次取出的零件是一等品的概率是．
(2)由（1）得，
因为，
所以，
所以．故在第1次取出的零件是一等品的条件下，第2次取出的零件也是一等品的概率为．
考点三 综合运用
【例3】 (2023·江苏扬州·高三期末）为了更好满足人民群众的健身和健康需求，国务院印发了《全民健身计划（）》．某中学为了解学生对上述相关知识的了解程度，先对所有学生进行了问卷测评，所得分数的分组区间为、、、、，由此得到总体的频率分布直方图，再利用分层抽样的方式随机抽取名学生进行进一步调研，已知频率分布直方图中、、成公比为的等比数列．
(1)若从得分在分以上的样本中随机选取人，用表示得分高于分的人数，求的分布列及期望；
(2)若学校打算从这名学生中依次抽取名学生进行调查分析，求在第一次抽出名学生分数在区间内的条件下，后两次抽出的名学生分数在同一分组区间的概率．
【答案】(1)分布列见解析，期望为；(2).
【解析】(1)解：由题意得，，因为，所以．
由分层抽样，抽出的名学生中得分位于区间内有人，
位于内有人，位于内有人，
位于内有人，位于区间学生有人，
这样，得分位于分以上的共有人，其中得分位于的有人，
所以的可能取值有、、，，，
所以的分布列为：
所以.
(2)解：记事件第一次抽出名学生分数在区间内，
记事件后两次抽出的名学生分数在同一分组区间内，
则，，
由条件概率公式可得.
【一隅三反】
1． (2023·全国·高三专题练习）某校从学生文艺部6名成员（4男2女）中，挑选2人参加学校举办的文艺汇演活动.
（1）求男生甲被选中的概率；
（2）在已知男生甲被选中的条件下，女生乙被选中的概率.
【答案】（1）；（2）.
【解析】记4名男生为，，，，2名女生为，，则从6名成员中挑选2名成员，有，，，，，，，，，，，，，，共15种情况.
（1）记“男生甲被选中”为事件，不妨假设男生甲为，事件所包含的基本事件为，，，，，共有5个，
∴.
（2）记“男生甲被选中”为事件，“女生乙被选中”为事件，不妨设男生甲为，女生乙为，则.
又由（1）知：，故.
2． (2023·辽宁沈阳·二模）甲、乙是北京2022冬奥会单板滑雪坡面障碍技巧项目的参赛选手，二人在练习赛中均需要挑战3次某高难度动作，每次挑战的结果只有成功和失败两种．
(1)甲在每次挑战中，成功的概率都为．设X为甲在3次挑战中成功的次数，求X的分布列和数学期望；
(2)乙在第一次挑战时，成功的概率为0.5，受心理因素影响，从第二次开始，每次成功的概率会发生改变其规律为：若前一次成功，则该次成功的概率比前一次成功的概率增加0.1；若前一次失败，则该次成功的概率比前一次成功的概率减少0.1．
（ⅰ）求乙在前两次挑战中，恰好成功一次的概率；
（ⅱ）求乙在第二次成功的条件下，第三次成功的概率．
【答案】(1)分布列见解析，(2)（ⅰ）0.4；（ⅱ）0.62．
【解析】(1)由题意得，，则，其中，
则X的分布列为：
则.
(2)设事件为“乙在第i次挑战中成功”，其中．
（ⅰ）设事件B为“乙在前两次挑战中，恰好成功一次”，则，
则
．
即乙在前两次挑战中，恰好成功一次的概为0.4．
（ⅱ）因为
，
且
，
所以．
即乙在第二次成功的条件下，第三次成功的概率为0.62．高一年级
高二年级
男同学
女同学
男同学
女同学
16
12
8
24
X
0
1
2
3
P