2024年新高考专用数学第一轮复习讲义一隅三反基础版 5.1 平面向量的线性运算及基本定理（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 5.1 平面向量的线性运算及基本定理（精讲）（基础版）（原卷版+解析版），共27页。试卷主要包含了概念辨析，共线定理，平面向量的基本定理，数量积，取值范围，平面向量与其他知识综合运用等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 概念辨析
【例1-1】 (2023·全国·高三专题练习）下列命题正确的是（ ）
A．向量与是相等向量
B．共线的单位向量是相等向量
C．零向量与任一向量共线
D．两平行向量所在直线平行
【例1-2】 (2023·全国·高三专题练习）下列命题中正确的是（ ）
A．若，则B．
C．与的方向相反D．若，则
【一隅三反】
1． (2023·全国·高三专题练习（理））下列说法错误的是（ ）
A．零向量与任一向量都平行B．方向相反的两个向量一定共线
C．单位向量长度都相等D．，，均为非零向量，若，则
2． (2023·全国·高三专题练习）给出如下命题：
①向量的长度与向量的长度相等；
②向量与平行，则与的方向相同或相反；
③两个有共同起点而且相等的向量，其终点必相同；
④两个公共终点的向量，一定是共线向量；
⑤向量与向量是共线向量，则点，，，必在同一条直线上．
其中正确的命题个数是（ ）
A．1B．2C．3D．4
3． (2023·全国·高三专题练习）（多选）下列命题中，不正确的是（ ）
A．若为单位向量，且，则
B．若，，则
C．
D．若平面内有四点，则必有
考点二 共线定理
【例2-1】 (2023·河南·平顶山市）已知向量，不共线，且向量与平行，则实数（ ）
A．B．C．D．
【例2-2】 (2023·山东潍坊·三模）已知，是平面内两个不共线的向量，，，，，则，，三点共线的充要条件是（ ）
A．B．C．D．
【一隅三反】
1 (2023·内蒙古）已知向量，是两个不共线的向量，与共线，则（ ）
A．2B．C．D．
2． (2023·山东泰安）已知向量，不共线，向量，，若O，A，B三点共线，则（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）①若，则与，共面；
②与，共面，则；
③若，则，，，四点共面；
④若，，，四点共面，则.
则以上结论中正确的有（ ）个
A．1B．2C．3D．4
考点三 平面向量的基本定理
【例3-1】 (2023·河南·平顶山市）如图，在平行四边形ABCD中，对角线AC与BD交于点O，且，则（ ）
A．B．C．D．
【例3-2】 (2023·青海·海东市）已知在中， ，，，则（ ）
A．B．C．D．1
【例3-3】 (2023·全国·高三专题练习）在中，D为三角形所在平面内一点，且，则（ ）
A．B．C．D．
【一隅三反】
1． (2023·吉林市）如图，中，，，点E是的三等分点，则（ ）
A．B．C．D．
2． (2023·安徽·合肥市第八中学）在平行四边形ABCD中，，G为EF的中点，则（ ）
A．B．
C．D．
3． (2023·全国·高三专题练习）在平行四边形中，分别是的中点，交于点，则（ ）
A．B．
C．D．
4． (2023·河南郑州）在中，是上一点，，是线段上一点，，则（ ）
A．B．C．D．
5． (2023·全国·高三专题练习）已知为内一点，，则，的面积之比为______．
6． (2023·全国·高三专题练习）若点是的重心，点、分别在、上，且满足，其中．若，则与的面积之比为_______．
考点四 数量积
【例4】 (2023·全国·高三专题练习）已知中，，，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得，则的值为（ ）
A．B．C．D．
【一隅三反】
1． (2023·北京·人大附中三模）在中，，点是的中点，则（ ）
A．B．7C．D．
2． (2023·四川·成都七中模拟预测（理））已知均为单位向量，且满足，则的值为（ ）
A．B．C．D．
3． (2023·江苏苏州）在中，，点D在线段上，点E在线段上，且满足，交于F，设，，则（ ）
A．B．C．D．
考点五 取值范围
【例5-1】 (2023·全国·高三阶段练习）在△ABC中，点D在线段BC的延长线上，且，点O在线段CD上（与点C，D不重合）．若，则x的取值范围是（ ）
A．B．
C．D．
【例5-2】． (2023·黑龙江·大庆实验中学）如图，在中，是线段上的一点，且，过点的直线分别交直线，于点，，若，，则的最小值是（ ）
A．B．C．D．
【一隅三反】
1． (2023·安徽阜阳）点M在边长为2的正三角形内（包括边界），满足，则的取值范围是（ ）
A．B．C．D．
2． (2023·湖北·十堰市教育科学研究院高三期末）已知正三角形ABC的边长为4，点P在边BC上，则的最小值为（ ）
A．2B．1C．D．
3． (2023·全国·高三专题练习）在中，，P为边AC上的动点，则的取值范围是（ ）
A．B．[12，16]
C．D．
4． (2023·全国·高三专题练习）已知直角梯形是边上的一点，则的取值范围为（ ）
A．B．C．D．
考点六 平面向量与其他知识综合运用
【例6-1】 (2023·全国·高三专题练习）在中，点是线段上任意一点（不包含端点），若，则的最小值是________.
【例6-2】 (2023·全国·高三专题练习）已知P是 的外心，且，则csC=（ ）
A．-B．-C．或-D．或-
【一隅三反】
1． (2023·全国·高三专题练习）如图，在中，M，N分别是线段，上的点，且，，D，E是线段上的两个动点，且，则的的最小值是（ ）
A．4B．C．D．2
2． (2023·全国·高三专题练习）集合，，则等于（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）直角三角形中，是斜边上一点，且满足，点、在过点的直线上，若，，，则下列结论错误的是（ ）
A．为常数B．的最小值为
C．的最小值为D．、的值可以为，
4． (2023·浙江·绍兴一中高三期末）已知点不共线，为实数，，则“”是“点在内（不含边界）”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
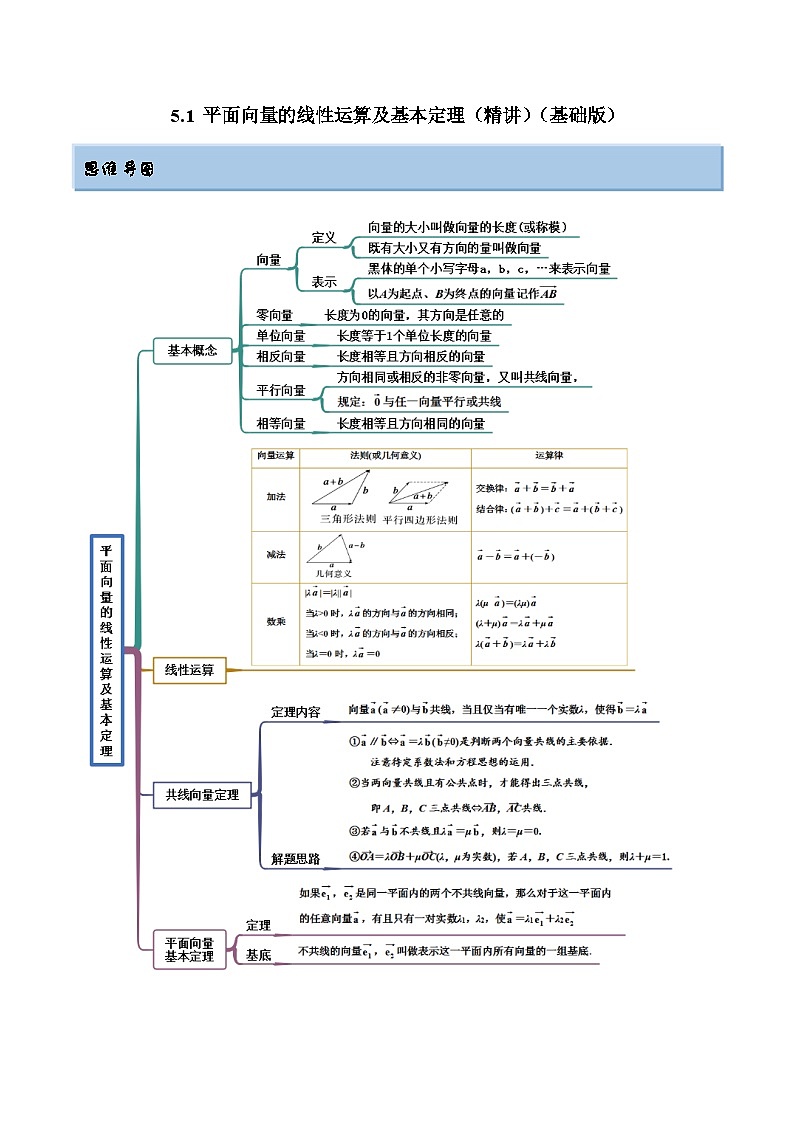
5.1 平面向量的线性运算及基本定理（精讲）（基础版）
思维导图
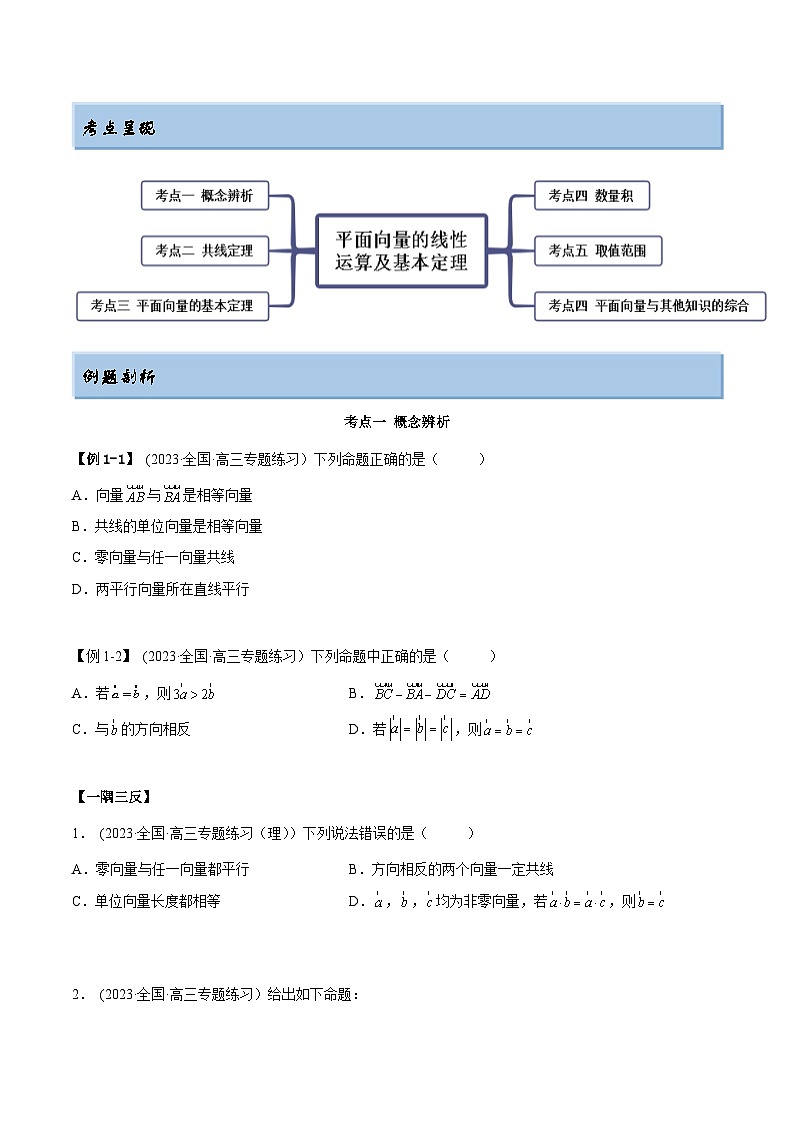
考点呈现
例题剖析
考点一 概念辨析
【例1-1】 (2023·全国·高三专题练习）下列命题正确的是（ ）
A．向量与是相等向量
B．共线的单位向量是相等向量
C．零向量与任一向量共线
D．两平行向量所在直线平行
【答案】C
【解析】对于A， ，故A错误；
对于B，两个单位向量虽然共线，但方向可能相反，故B错误；
对于C，因为零向量没有方向，所以与任何向量都是共线的，故C正确；
对于D，两个平行向量所在的直线可能重合，故D错误；故选：C.
【例1-2】 (2023·全国·高三专题练习）下列命题中正确的是（ ）
A．若，则B．
C．与的方向相反D．若，则
【答案】B
【解析】对于A选项，由于任意两个向量不能比大小，故A错；
对于B选项，，故B对；
对于C选项，与的方向相同，故C错；
对于D选项，若，但、、的方向不确定，故D错.故选：B.
【一隅三反】
1． (2023·全国·高三专题练习（理））下列说法错误的是（ ）
A．零向量与任一向量都平行B．方向相反的两个向量一定共线
C．单位向量长度都相等D．，，均为非零向量，若，则
【答案】D
【解析】规定：零向量与任一向量都平行，故A正确；
方向相反的两个向量一定共线，故B正确；
单位向量长度都为1，故C正确；
当时，且成立，但不一定成立，故D错误；故选：D.
2． (2023·全国·高三专题练习）给出如下命题：
①向量的长度与向量的长度相等；
②向量与平行，则与的方向相同或相反；
③两个有共同起点而且相等的向量，其终点必相同；
④两个公共终点的向量，一定是共线向量；
⑤向量与向量是共线向量，则点，，，必在同一条直线上．
其中正确的命题个数是（ ）
A．1B．2C．3D．4
【答案】B
【解析】对于①，向量与向量，长度相等，方向相反，故①正确；
对于②，向量与平行时，或为零向量时，不满足条件，故②错误；
对于③，两个有共同起点且相等的向量，其终点也相同，故③正确；
对于④，两个有公共终点的向量，不一定是共线向量，故④错误；
对于⑤，向量与是共线向量，点，，，不一定在同一条直线上，故⑤错误．
综上，正确的命题是①③．故选：B．
3． (2023·全国·高三专题练习）（多选）下列命题中，不正确的是（ ）
A．若为单位向量，且，则
B．若，，则
C．
D．若平面内有四点，则必有
【答案】ABC
【解析】对于A，，与同向或反向，或，A错误；
对于B，若，则，，但与可能不共线，B错误；
对于C，，C错误；
对于D，，，D正确.故选：ABC.
考点二 共线定理
【例2-1】 (2023·河南·平顶山市）已知向量，不共线，且向量与平行，则实数（ ）
A．B．C．D．
【答案】B
【解析】与平行，，向量不共线，
∴存在实数k，使得，，解得，故选：B．
【例2-2】 (2023·山东潍坊·三模）已知，是平面内两个不共线的向量，，，，，则，，三点共线的充要条件是（ ）
A．B．C．D．
【答案】C
【解析】由，，三点共线的充要条件是且，所以，故.故选：C
【一隅三反】
1 (2023·内蒙古）已知向量，是两个不共线的向量，与共线，则（ ）
A．2B．C．D．
【答案】C
【解析】因为与共线，所以，，
所以，
因为向量，是两个不共线的向量，所以，解得，故选：C．
2． (2023·山东泰安）已知向量，不共线，向量，，若O，A，B三点共线，则（ ）
A．B．C．D．
【答案】A
【解析】因为O，A，B三点共线，则所以，，即
整理得：又∵向量，不共线，则，则故选：A．
3． (2023·全国·高三专题练习）①若，则与，共面；
②与，共面，则；
③若，则，，，四点共面；
④若，，，四点共面，则.
则以上结论中正确的有（ ）个
A．1B．2C．3D．4
【答案】B
【解析】在①中， ，则由平面向量基本定理得与，一定在同一平面内，故①正确；
在②中，若与，共面，，但如果，共线， 就不一定能用，来表示，故②错误；
在③中，若，则三向量在同一平面内，所以M、N、A、B四点共面，故③正确；
在④中，若M、P、A、B四点共面，且M、P、A、B共线，则不一定成立，故④错误.
故选:B
考点三 平面向量的基本定理
【例3-1】 (2023·河南·平顶山市）如图，在平行四边形ABCD中，对角线AC与BD交于点O，且，则（ ）
A．B．C．D．
【答案】C
【解析】因为，所以，
所以.故选：C.
【例3-2】 (2023·青海·海东市）已知在中， ，，，则（ ）
A．B．C．D．1
【答案】A
【解析】因为，所以，
因为，所以，
又，所以，
又，所以，得．故选：A
【例3-3】 (2023·全国·高三专题练习）在中，D为三角形所在平面内一点，且，则（ ）
A．B．C．D．
【答案】B
【解析】如图，设AD交BC于E，且，由B,E,C三点共线可得：
，∴，
∴.
设，则，∴.
又，∴，∴.故选：B.
【一隅三反】
1． (2023·吉林市）如图，中，，，点E是的三等分点，则（ ）
A．B．C．D．
【答案】B
【解析】故选：B.
2． (2023·安徽·合肥市第八中学）在平行四边形ABCD中，，G为EF的中点，则（ ）
A．B．
C．D．
【答案】B
【解析】．故选：B.
3． (2023·全国·高三专题练习）在平行四边形中，分别是的中点，交于点，则（ ）
A．B．
C．D．
【答案】B
【解析】如图，
过点作的平行线交于，
则是的中点，且，，
又，所以，即，所以，
又，故选：B
4． (2023·河南郑州）在中，是上一点，，是线段上一点，，则（ ）
A．B．C．D．
【答案】D
【解析】因为，则，所以，，
，
因为是线段上一点，设，其中，
所以，，解得.故选：D.
5． (2023·全国·高三专题练习）已知为内一点，，则，的面积之比为______．
【答案】
【解析】如图所示，由，得，
取为中点，为中点，则，所以．故答案为：.
6． (2023·全国·高三专题练习）若点是的重心，点、分别在、上，且满足，其中．若，则与的面积之比为_______．
【答案】
【解析】设的中点为，则,
因为，所以,所以，
因为，所以，因为，所以，所以，所以，
所以故答案为：
考点四 数量积
【例4】 (2023·全国·高三专题练习）已知中，，，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得，则的值为（ ）
A．B．C．D．
【答案】B
【解析】如图所示，根据向量的线性运算法则，可得，
因为，且为的中点，可得，所以，
又因为点D，E分别是边AB，BC的中点，且，所以，
则.故选：B.
【一隅三反】
1． (2023·北京·人大附中三模）在中，，点是的中点，则（ ）
A．B．7C．D．
【答案】A
【解析】在中，点是的中点，所以,,
所以.故选：A
2． (2023·四川·成都七中模拟预测（理））已知均为单位向量，且满足，则的值为（ ）
A．B．C．D．
【答案】B
【解析】，同理
．故选：B.
3． (2023·江苏苏州）在中，，点D在线段上，点E在线段上，且满足，交于F，设，，则（ ）
A．B．C．D．
【答案】B
【解析】设，，因为
所以有，
因此，
因为，，，所以，故选：B
考点五 取值范围
【例5-1】 (2023·全国·高三阶段练习）在△ABC中，点D在线段BC的延长线上，且，点O在线段CD上（与点C，D不重合）．若，则x的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】
设，因为，点O在线段CD上（与点C，D不重合），所以，
所以
因为，所以，所以.故选：C．
【例5-2】． (2023·黑龙江·大庆实验中学）如图，在中，是线段上的一点，且，过点的直线分别交直线，于点，，若，，则的最小值是（ ）
A．B．C．D．
【答案】C
【解析】由条件可得，
∵∴，
因为三点共线，∴，∴，
∵，∴，则；
当且仅当，即时取等号，故的最小值是；故选：C．
【一隅三反】
1． (2023·安徽阜阳）点M在边长为2的正三角形内（包括边界），满足，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】因为点M是正三角形内的一点（包括边界），所以，由.故选：B.
2． (2023·湖北·十堰市教育科学研究院高三期末）已知正三角形ABC的边长为4，点P在边BC上，则的最小值为（ ）
A．2B．1C．D．
【答案】D
【解析】记，
因为，所以.故选：D
3． (2023·全国·高三专题练习）在中，，P为边AC上的动点，则的取值范围是（ ）
A．B．[12，16]
C．D．
【答案】B
【解析】因为P在AC上，所以，其中，
则
，
因为，所以.故选：B
4． (2023·全国·高三专题练习）已知直角梯形是边上的一点，则的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】法一：因为在上，不妨设，
则（其中）
所以
，
因为，所以
法二：如图，以点A为坐标原点，AB所在直线为x轴，AD所在直线为y轴建立直角坐标系.则，，，，其中∠ABC=45°，设点，
其中，，
∴
∵
∴
故选：D.
考点六 平面向量与其他知识综合运用
【例6-1】 (2023·全国·高三专题练习）在中，点是线段上任意一点（不包含端点），若，则的最小值是________.
【答案】9
【解析】∵是线段上一点,∴三点共线，
∴ m ＋ n = 1 , 且 m > 0 , n > 0 ,
当且仅当 即
又∵ ∴时取等号，的最小值为 9 .故答案为：9
【例6-2】 (2023·全国·高三专题练习）已知P是 的外心，且，则csC=（ ）
A．-B．-C．或-D．或-
【答案】B
【解析】因为P是的外心，所以，
由题知，两边平方得
即,即，
所以，则，
又由，得，
因为，则C与外心P在AB的异侧，即C在劣弧上，所以C为钝角，即.故选：B
【一隅三反】
1． (2023·全国·高三专题练习）如图，在中，M，N分别是线段，上的点，且，，D，E是线段上的两个动点，且，则的的最小值是（ ）
A．4B．C．D．2
【答案】B
【解析】设，，，，
则，，，，.
所以，
当且仅当，时等号成立.
所以的的最小值是.故选：B
2． (2023·全国·高三专题练习）集合，，则等于（ ）
A．B．C．D．
【答案】B
【解析】由题意，集合
集合
要求解两个向量的交集，即找出两个向量集合中的相同元素，
因为元素是向量，要使的向量相等，只有横标和纵标分别相等，
所以，解得，此时．故选：B．
3． (2023·全国·高三专题练习）直角三角形中，是斜边上一点，且满足，点、在过点的直线上，若，，，则下列结论错误的是（ ）
A．为常数B．的最小值为
C．的最小值为D．、的值可以为，
【答案】B
【解析】如下图所示：
由，可得，
，
若，，，
则，，
，
、、三点共线，
，，
故A正确；
所以，时，也满足，则D选项正确；
，当且仅当时，等号成立，C选项成立；
，当且仅当时，即，时等号成立，故B选项错误.
故选：B
4． (2023·浙江·绍兴一中高三期末）已知点不共线，为实数，，则“”是“点在内（不含边界）”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【解析】若，且，可知三点共线，
若，点在内部（不含边界），则；
反之不成立，例如时，此时在外部，
所以“”是“点在内（不含边界）”的必要不充分条件，故选：B.