2024年高考数学小专题特训：空间向量与立体几何解答题

这是一份2024年高考数学小专题特训：空间向量与立体几何解答题，共19页。试卷主要包含了已知向量 a=，b=，c= .等内容，欢迎下载使用。
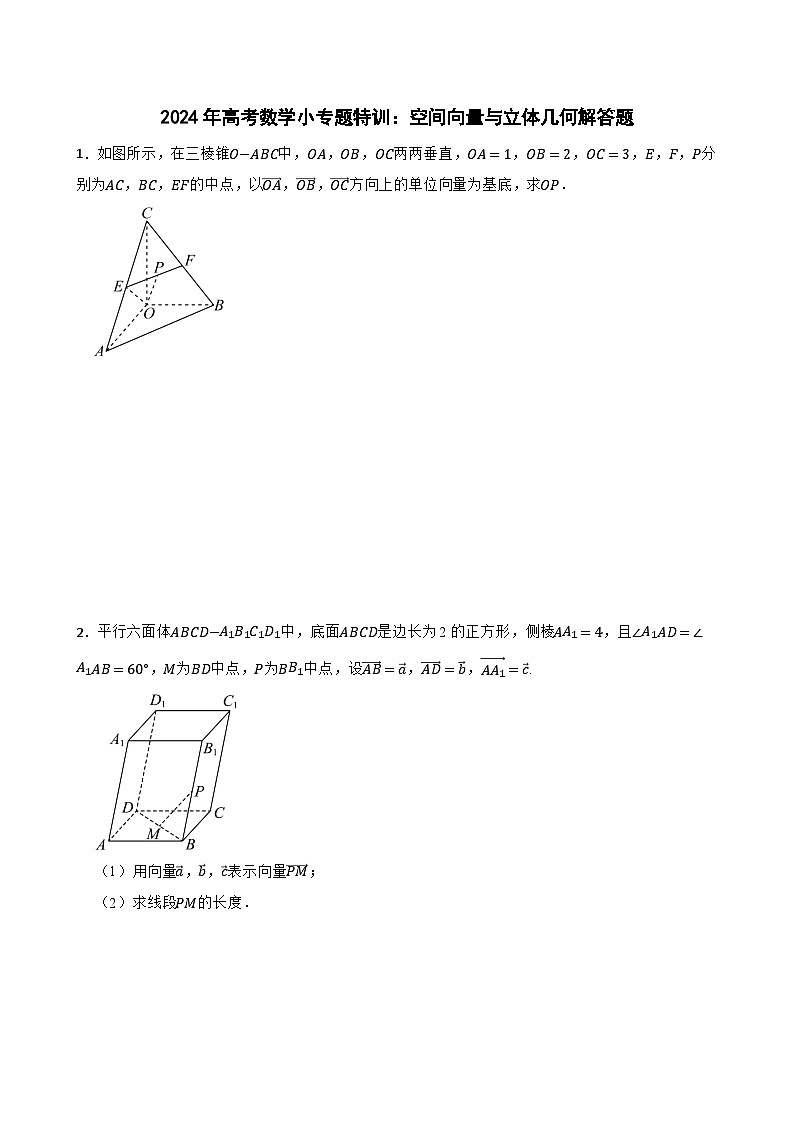
1．如图所示，在三棱锥O−ABC中，OA，OB，OC两两垂直，OA=1，OB=2，OC=3，E，F，P分别为AC，BC，EF的中点，以OA，OB，OC方向上的单位向量为基底，求OP．
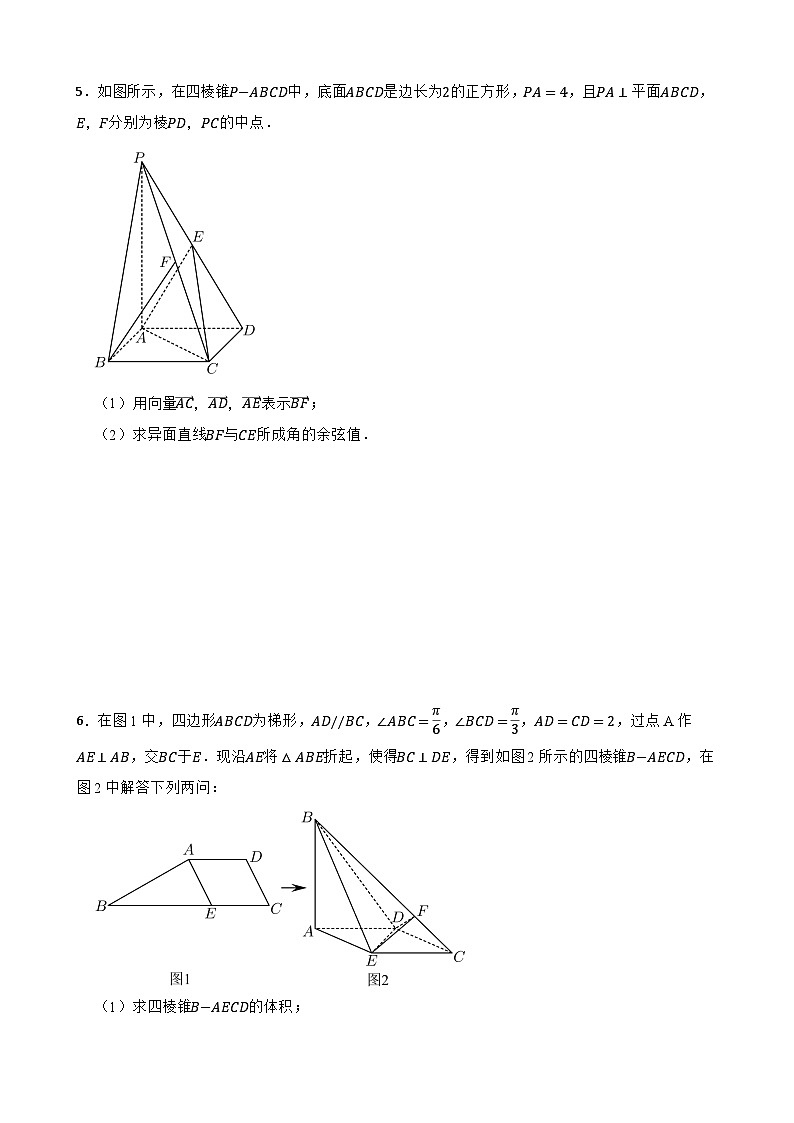
2．平行六面体ABCD−A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1=4，且∠A1AD=∠A1AB=60°，M为BD中点，P为BB1中点，设AB=a，AD=b，AA1=c.
（1）用向量a，b，c表示向量PM；
（2）求线段PM的长度．
3．如图，已知平行六面体ABCD−A1B1C1D1的侧棱长为3，底面是边长为4的菱形，且∠A1AD=∠A1AB=∠DAB=π3，点E，F分别在B1B和D1D上．
（1）若BE=13BB1，DF=23DD1，求证：A，E，C1，F四点共面；
（2）求VA1−AEF；
（3）若BE=13BB1，点F为线段DD1上（包括端点）的动点，求直线EF与平面ABB1A1所成角的正弦值的取值范围．
4．如图，在四棱锥P−ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AB=1，PA=2，点E为BC的中点，点H在线段PD上且DH=13DP．
（1）用向量AB，AD，AP表示向量PE；
（2）求EH的长．
5．如图所示，在四棱锥P−ABCD中，底面ABCD是边长为2的正方形，PA=4，且PA⊥平面ABCD，E，F分别为棱PD，PC的中点．
（1）用向量AC，AD，AE表示BF；
（2）求异面直线BF与CE所成角的余弦值．
6．在图1中，四边形ABCD为梯形，AD//BC，∠ABC=π6，∠BCD=π3，AD=CD=2，过点A作AE⊥AB，交BC于E．现沿AE将△ABE折起，使得BC⊥DE，得到如图2所示的四棱锥B−AECD，在图2中解答下列两问：
（1）求四棱锥B−AECD的体积；
（2）若F在侧棱BC上，BF=34BC，求证：二面角C−EF−D为直二面角．
7．如图，三棱台ABC−A1B1C1，AB⊥BC，AC⊥BB1，平面ABB1A1⊥平面ABC，AB=6， BC=4，BB1=2，AC1与A1C相交于点D，AE=2EB，且DE∥平面BCC1B1．
（1）求三棱锥C−A1B1C1的体积；
（2）求直线CC1与平面A1B1C所成角的正弦值．
8．如图所示，在四棱锥P−ABCD中，△PBC为等腰直角三角形，且∠CPB=90°，四边形ABCD为直角梯形，满足AD//BC，CD⊥AD，BC=CD=2AD=4，PD=26．
（1）若点F为DC的中点，求cs⟨AP，BF⟩；
（2）若点E为PB的中点，点M为AB上一点，当EM⊥BF时，求|AM||AB|的值．
9．已知向量 a=(2，4，−2)，b=(−1，0，2)，c=(x，2，−1) .
（1）若 a ∥ c ，求 |c| ；
（2）若 b⊥c ，求 (a−c)⋅(2b+c) 的值.
10．如图，在三棱柱 ABC−A1B1C1 中， ∠ABC=90° ， AB=1 ， BB1=BC=23 ， B1 在平面 ABC 的射影 H 为 BC 中点，以 H 为坐标原点， HC 的方向为 x 轴的正方向， HB1 的方向为 z 轴的正方向，建立如图所示的空间直角坐标系 H−xyz ．
（1）分别求 A1 ， B1 ， C1 点坐标；
（2）求四棱锥 B−ACC1A1 的高．
11．如图，在四棱锥P−ABCD中，PA⊥平面ABCD，AB∥CD，且CD=2，AB=1，BC=22，PA=1，AB⊥BC，N为PD的中点.
（1）求平面PAD与平面PBC所成夹角的余弦值；
（2）求点N到直线BC的距离；
（3）在线段PD上是否存在一点M，使得直线CM与平面PBC所成角的正弦值为2626，若存在，求出DMDP的值；若不存在，说明理由.
12．如图，在几何体P−ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC=∠BAD=π2，AD=2，AB=BC=1．
（1）求证：CD⊥平面PAC；
（2）若PC与平面ABCD所成角为π3，求点A到平面PCD的距离．
13．如图，在底面是菱形的四棱锥P−ABCD中，PA⊥底面ABCD，PA=AC=6，∠ABC=60∘，E是棱PD上一点，且PE=2DE
（1）求二面角E−AC−D的大小
（2）在棱PC上是否存在一点F，使得BF//平面ACE？证明你的结论。
14．如图，在四棱锥P−ABCD中，PA⊥平面ABCD，PA=2，底面ABCD为直角梯形，∠BAD=90°，AB=2，CD=AD=1，N是PB的中点，点M，Q分别在线段PD与AP上，且DM=λMP，AQ=μQP.
（1）当λ=1时，求平面MDN与平面DNC的夹角大小；
（2）若MQ∥平面PBC，证明：μ=1+2λ.
答案解析部分
1．【答案】解：令OA，OB，OC方向上的单位向量分别为m，j，k，则{i，j，k}是单位正交基底．
因为OP=OE+EP=12(OA+OC)+12EF==12(OA+OC)+14AB
=12(OA+OC)+14(OB−OA)
=14OA+14OB+12OC=14i+14×2j+12×3k
=14i+12j+32k，
所以|OP|=(14i+12j+32k)2=116+14+94=414，
所以OP的长度为414．
2．【答案】（1）解：因为M为BD中点，P为BB1中点，AB=a，AD=b，AA1=c，
所以PM=PB+BM=12B1B+12BD=−12BB1+12(AD−AB)
=12AD−12AB−12BB1=12(AD−AB−AA1)=12(b−a−c)
（2）解：因为平行六面体ABCD−A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1=4，且∠A1AD=∠A1AB=60°，
所以|a|=|b|=2，|c|=4，a⋅b=0，a⋅c=b⋅c=2×4×12=4，
所以PM2=14(b−a−c)2=14(b2+a2+c2−2a⋅b−2b⋅c+2a⋅c)
=14×(4+4+16−0−8+8)=6
所以|PM|=6，即线段PM长为6
3．【答案】（1）证明：∵AC1=AB+AD+AA1，AE=AB+13AA1，AF=AD+23AA1，
∴AE+AF=AC1，所以A，E，C1，F四点共面.
（2）解：∵BB1//平面AA1D1D，
∴BB1上的所有的点到平面AA1D1D的距离都相等，
同理DD1上所有的点到AA1B1B的距离也相等，
∴VA1−AEF=VF−A1EA=VA1−ABD=16VA1B1C1D1−ABCD，
∵∠A1AD=∠A1AB=∠DAB=π3，
∴点A1在平面ABCD的射影落在AC上，过点A1作A1G⊥AC，过点G作GH⊥AB，
∵A1G⊥平面ABCD，
∴A1G⊥AB，又A1G与GH是平面A1GH内两条相交直线，
∴AB⊥平面A1GH，∴AB⊥A1H，在直角三角形A1HA中，∠A1AH=60，
A1A=3，解得AH=32，
又在直角三角形AHG中，∠HAG=30，∴AG=3，
在直角三角形A1GA中，可得A1G=6，
∴VA1−AEF=VA−A1EF=VA1−ABD=16VA1B1C1D1−ABCD=16×SABCD×A1G=42；
（3）解：设AB与CD的交点为O，以点O为坐标原点，建立如图所示空间直角坐标系，由（2）可知AG=3，A1G=6，
∴A1(3，0，6)，A(23，0，0)，D(0，−2，0)，B(0，2，0)，
由AA1=DD1=BB1，可求得D1(−3，−2，6)，B1(−3，2，6)，
∴AB=(−23，2，0)，AA1=(−3，0，6)，
设n=(x，y，z)为平面A1AB的法向量，
∴−23x+2y=0−3x+6z=0，取z=2，∴x=2，y=23，
∴n=(2，23，2)，
∵BE=13BB1，∴E(−33，2，63)，
设DF=λDD1(0≤λ≤1)，∴F(−3λ，−2，6λ)，
∴EF=(−3λ+33，−4，6λ−63)，
设直线EF与平面ABB1A1所成角的为θ，
∴sinθ=|EF⋅n|EF||n||=|−8332×9λ2−6λ+17|=4639λ2−6λ+17，
∵0≤λ≤1，16≤9λ2−6λ+17≤20，
∴sinθ∈[23015，63]．
4．【答案】（1）因为点E为BC的中点，所以BE=12BC=12AD，
所以PE=PA+AB+BE=AB+12AD−AP；
（2）因为点H在线段PD上且DH=13DP，
所以PH=23PD，
所以PH=23PD=23(AD−AP)=23AD−23AP，
所以EH=PH−PE=16AD−AB+13AP，
因为在四棱锥P−ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AB，AD⊂底面ABCD
所以AB⊥AD，PA⊥AB，PA⊥AD，
则AD⋅AB=AD⋅AP=AB⋅AP=0，
∴|EH|2=(16AD−AB+13AP)2
=136AD2+AB2+19AP2−13AD⋅AB+19AD⋅AP−23AB⋅AP=136+1+49=5336，
∴|EH|=536．
5．【答案】（1）解：BF=BC+CF=AD+12CP=AD+12(CD+DP)=AD+12(AD−AC)+12DP=AD+12(AD−AC)+DE=AD+12(AD−AC)+AE−AD=12AD−12AC+AE.
（2）解：以A为坐标原点，AB，AD，AP正方向为x，y，z轴，可建立如图所示空间直角坐标系，
则B(2，0，0)，C(2，2，0)，F(1，1，2)，E(0，1，2)，∴BF=(−1，1，2)，CE=(−2，−1，2)，
∴|cs|=|BF⋅CE||BF|⋅|CE|=56×3=5618，
即异面直线BF与CE所成角的余弦值为5618.
6．【答案】（1）解：在图1中，∵∠ABC=π6，AE⊥AB，∴∠AEB=π3，
又∠BCD=π3，∴AE//CD，
又AD//BC，
∴四边形AECD为平行四边形，
∵AD=CD，
∴平行四边形AECD为菱形．
在图2中，连接AC，则DE⊥AC，
又BC⊥DE，AC，BC⊂平面ABC，
AC∩BC=C，∴DE⊥平面ABC，
∵AB⊂平面ABC，∴AB⊥DE
∵AE⊥AB，AE∩DE=E，AE，DE⊂平面AECD，
∴AB⊥平面AECD
VB−AECD=13SAECD×AB=13×(AD×AEsinπ3)×(AEtanπ3)=4
（2）解：在图2中，以A为原点，以AD所在的直线为y轴建立如图所示的直角坐标系，则B(0，0，23)，D(0，2，0)，E(3，1，0)，C(3，3，0)，
EF=EB+BF=EB+34BC=(−3，−1，23)+34(3，3，−23)=(−34，54，32)
设面CEF的一个法向量为n1=(x1，y1，z1)，EC=(0，2，0)，
由n1⋅EC=0n1⋅EF=0⇒2y1=0−34x1+54y1+32z1=0
令z1=1，则x1=2，y1=0，取n1=(2，0，1)
设面DEF的一个法向量为n2=(x2，y2，z2)，ED=(−3，1，0)，
由n2⋅ED=0n2⋅EF=0⇒−3x2+y2=0−34x2+54y2+32z2=0
令x2=1，则y2=3，z2=−2，取n2=(1，3，−2)
所以n1⋅n2=0，∴n1⊥n2，从而二面角C−EF−D为直二面角
7．【答案】（1）解：由题意，∵平面ABB1A1⊥平面ABC，且平面ABB1A1∩平面ABC=AB，AB⊥BC，BC⊂平面ABC，
∴BC⊥平面ABB1A1，
∵BB1⊂平面ABB1A1，
∴BC⊥BB1，
又AC⊥BB1，BC∩AC=C，
BC，AC⊂平面ABC，
∴BB1⊥平面ABC，
连接C1B，
∵DE//平面BCC1B1，
DE⊂平面ABC1，
平面ABC1∩平面BCC1B1=C1B，
∴DE∥C1B，
∵AE=2EB，
∴AD=2DC1，
∴A1C1=12AC．
∴三棱锥C−A1B1C1底面A1B1C1的面积S1=12×2×3=3，
高ℎ=BB1=2，
∴其体积为：V=13S1ℎ=13×3×2=2．
（2）证明：由题意及（1）得，以B为坐标原点，分别以BA，BC，BB1为x，y，z轴的正方向建立空间直角坐标系，如图．
A(6，0，0)，C(0，4，0)，B1(0，0，2)，A1(3，0，2)，C1(0，2，2)，
则B1A1=(3，0，0)，B1C=(0，4，−2)，CC1=(0，−2，2)．
设平面A1B1C的法向量为n=(x，y，z)，
由n⋅B1A1=3x=0n⋅B1C=4y−2z=0，
取y=1，则x=0，z=2
所以n=(0，1，2)，
设CC1与平面A1B1C所成角为β，
所以sinβ=|n⋅CC1||n||CC1|=25×22=1010．
8．【答案】（1）解：因为△PBC为等腰直角三角形，∠CPB=90°，BC=CD=4，所以PC=PB=22，
又PD2=(26)2=24，PC2+CD2=(22)2+42=24，所以DC⊥PC．
而CD⊥AD，CD//BC，故CD⊥BC，
因PC∩BC=C，PC，BC⊂平面PBC，故CD⊥平面PBC.
以点C为原点，CP，CD所在直线分别为x，z轴，过点C作PB的平行线为y轴，建立空间直角坐标系C−xyz，如图所示．
则P(22，0，0)，B(22，22，0)，F(0，0，2)，A(2，2，4)，B(22，22，0)．
则AP=(2，−2，−4)，BF=(−22，−22，2)，
所以cs⟨AP，BF⟩=AP⋅BF|AP|⋅|BF|=2×(−22)+(−2)×(−22)+(−4)×225×25=−25．
（2）解：由（1）知E(22，2，0)，设AM=tAB，
而AB=(2，2，−4)，所以AM=(2t，2t，−4t)，
所以M(2+2t，2+2t，4−4t)，所以EM=(2t−2，2t，4−4t)，
又BF=(−22，−22，2)，
因为EM⊥BF，故EM⋅BF=0，
所以−22×(2t−2)−22×2t+8−8t=0，解得t=34，
所以|AM||AB|=34．
9．【答案】（1）∵ a ∥ c ，
∴ x2=24=−1−2 ，
∴ x=1 ，
∴ c=（1，2，−1） ，
|c|=6 .
（2）∵ b⊥c ，
∴ −x+2×0−1×2=0 ，
∴ x=−2 ，
∴ c=(−2，2，−1) ，
∴ a−c=(4，2，−1) ， 2b+c=(−4，2，3) ，
∴ (a−c)⋅(2b+c)=−15
10．【答案】（1）解：因为 B1 在平面 ABC 的射影 H 为 BC 中点，所以 B1H⊥ 平面 ABC ．
又 BB1=BC=23 ，所以 BH=3，B1H=3 ．
则 A(−3，1，0) ， B(−3，0，0) ， C(3，0，0) ， B1(0，0，3) ， C1(23，0，3) ，
设 A1(x，y，z) ，由已知得 AA1=BB1=(3，0，3) ，即 (x+3，y−1，z)=(3，0，3) ，
解得 x=0 ， y=1 ， z=3 ， A1(0，1，3)
（2）解：四棱锥 B−ACC1A1 的高为 B 到平面 ACC1A1 的距离． CC1=(3，0，3) ， AC=(23，−1，0) ．
设平面 ACC1A1 的法向量为 n=(x，y，z) ，则 CC1⋅n=0AC⋅n=0 ，即 3x+3z=023x−y=0 ，
令 z=−1 ，可得 x=3 ， y=6 ，所以可取 n=(3，6，−1) ．
BA=(0，1，0) ， B 到平面 ACC1A1 的距离 d=|BA⋅n||n|=|6|3+36+1=31010 ．
所以四棱锥 B−ACC1A1 的高为 31010
11．【答案】（1）解：如图所示：Q为CD中点，连接AQ，
则AB=CQ=1，AB∥CQ，AB⊥BC，
则四边形ABCQ为矩形，故AQ⊥AB，
以AQ，AB，AP为x，y，z轴建立空间直角坐标系，
则A(0，0，0)，B(0，1，0)，C(22，1，0)，D(22，−1，0)，P(0，0，1)，N(2，−12，12).
设平面PAD的法向量为n1=(x1，y1，z1)，则AP⋅n1=z1=0AP⋅n1=22x1−y1=0，
取x1=1得到n1=(1，22，0)，
设平面PBC的法向量为n2=(x2，y2，z2)，则BC⋅n2=22x2=0BP⋅n2=−y2+z2=0，
取y2=1得到n2=(0，1，1)，
故平面PAD与平面PBC所成角的余弦值为|cs⟨n1，n2⟩|=|n1⋅n2||n1|⋅|n2|=2232=23.
（2）解：BN=(2，−32，12)，BC=(22，0，0)，则cs⟨BN，BC⟩=BN⋅BC|BN|⋅|BC|=4322×22=23，
⟨BN，BC⟩∈[0，π]，故，
点N到直线BC的距离为|BN|sin⟨BN，BC⟩=322×53=102
（3）解：令DM=λDP，λ∈[0，1]，
设M(x，y，z)，则(x−22，y+1，z)=λ(−22，1，1)，
则M(22−22λ，λ−1，λ)，即CM=(−22λ，λ−2，λ)，
平面PBC的一个法向量n2=(0，1，1)，故2626=|CM⋅n2||CM|⋅|n2|=|2λ−2|28λ2+(λ−2)2+λ2，21λ2−50λ2+24=0，
解得λ=23或λ=127（舍），
故存在点M满足条件，DMDP=23.
12．【答案】（1）证明略
（2）解：点A到平面PCD的距离为62．
13．【答案】（1）解：取BC的中点为G，连接AG，
因为在底面为菱形的四棱锥P−ABCD中，PA⊥底面ABCD，PA=AC=6，∠ABC=60∘
所以AG⊥BD，AG=62−32=33
以A为原点，AG，AD，AP为x，y，z轴，建立空间直角坐标系
则A(0，0，0)，C(33，3，0)，D(0，6，0)，P(0，0，6)
因为点E在PD上，且PE=2DE，∴E(0，4，2)
AE=(0，4，2)，AC=(33，3，0)
设平面ACE的法向量为n=(x，y，z)
则n⋅AC=33x+3y=0n⋅AE=4x+2y=0，取x=1，得n=(1，−3，−2)
平面ACD的法向量为m=(0，0，1)
设二面角E−AC−D的大小为θ
则csθ=|m⋅n||m|⋅|n|=28=22，∴θ=π4
则二面角E−AC−D的大小为π4
（2）解：设在棱PC上存在点F(a，b，c)，且PF=λPC，0≤λ≤1，使得BF//平面ACE
则(a，b，c−1)=(32λ，12λ，−λ)，解得F(32λ，12λ，−λ)
因为B=(32，−12，0)，所以BF→(32λ−32，12λ+12，1−λ)，
因为平面ACE的法向量(1，−3，−2)，BF//平面ACE
所以BF→⋅n→=32λ−32−32λ−32−2+2λ=0
解得λ=1+32∉(0，1)
则在棱PC上不存在一点F，使得BF//平面ACE
14．【答案】（1）解：建立如图所示的空间直角坐标系，则D(1，0，0)，C(1，1，0)，B(0，2，0)，P(0，0，2).
当λ=1时，M(12，0，1)，N(0，1，1)，
则MN=(−12，1，0)，DN=(−1，1，1)，CN=(−1，0，1).
设平面MDN的法向量为m=(x，y，z)，平面DNC的法向量为n=(a，b，c)，
∴−12x+y=0且−x+y+z=0，−a+c=0且−a+b+c=0，令y=1，a=1，
则m=(2，1，1)，n=(1，0，1)，
∴cs⟨m，n⟩=36×2=32，
∴平面MDN与平面DNC的夹角大小为30°.
（2）证明：设M(x′，y′，z′)，由DM=λMP，得(x′−1，y′，z′)=λ(−x′，−y′，2−z′)，
∴M(11+λ，0，2λ1+λ)，
同理由AQ=μQP，得Q(0，0，2μ1+μ)，∴MQ=(−11+λ，0，2μ1+μ−2λ1+λ).
PB=(0，2，−2)，BC=(1，−1，0)，设平面PBC的法向量为p=(x1，y1，z1)，
∴2y1−2z1=0且x1−y1=0，令x1=1，则p=(1，1，1)，
∴p⋅MQ=0，则−11+λ+2μ1+μ−2λ1+λ=0，即μ=1+2λ .