四川省宜宾市兴文县2023-2024学年九年级上学期期末数学试题（原卷版+解析版）

这是一份四川省宜宾市兴文县2023-2024学年九年级上学期期末数学试题（原卷版+解析版），文件包含精品解析四川省宜宾市兴文县2023-2024学年九年级上学期期末数学试题原卷版docx、精品解析四川省宜宾市兴文县2023-2024学年九年级上学期期末数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
注意事项：
1．答题前，考生务必将自己的学校、班级、姓名、准考证号填写在答题卡规定的位置上．
2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．
3．答非选择题时，必须使用黑色墨水笔或黑色签字笔，将答案书写在答题卡规定的位置上．
4．所有题目必须在答题卡规定的位置上作答，在试卷上答题无效．
5．考试结束后，将本试卷和答题卡一并交回．
一、选择题（本大题共12小题，每小题4分，共48分．在每小题所给的四个选项中，有且只有一项是符合题目要求的）
1. 下列方程一定是一元二次方程的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了一元二次方程的定义，掌握一元二次方程的定义是解题的关键．
根据一元二次方程的定义逐项分析判断即可求解，一元二次方程定义，只含有一个未知数，并且未知数项的最高次数是2的整式方程叫做一元二次方程．
【详解】A. ，是一元一次方程，故该选项不正确，不符合题意；
B. ，当时，是一元二次方程，故该选项不正确，不符合题意；
C. ，不是整式方程，故该选项不正确，不符合题意；
D. ，是一元二次方程，故该选项正确，符合题意；
故选：D．
2. 等于（ ）
A. B. C. D.
【答案】A
【解析】
【分析】直接利用特殊角的三角函数值求出答案．
详解】解：．
故选：A．
【点睛】此题主要考查了特殊角的三角函数值，解题的关键是正确记忆相关特殊角的三角函数值．
3. 下列二次根式中，是最简二次根式的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了最简二次根式的知识，解答本题的关键在于掌握最简二次根式的概念，对各选项进行判断．根据最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式，结合选项求解即可．
【详解】解：A、是最简二次根式，符合题意；
B、，故不是最简二次根式，不符合题意；
C、，故不是最简二次根式，不符合题意；
D、，故不是最简二次根式，不符合题意．
故选：A．
4. 一个口袋中装有分别写有“兴文”“石海”字小球共20个，它们除此之外完全相同．将口袋中的球搅拌均匀后从中随机摸出一个球，记下上面的字后，再放回口袋中搅匀，不断重复这一过程，发现摸到“兴文”球的频率稳定在左右，则估计这个口袋中“兴文”球的个数为（ ）
A. 14个B. 13个C. 7个D. 6个
【答案】B
【解析】
【分析】此题主要考查了利用频率估计概率，本题利用了用大量试验得到的频率可以估计事件的概率．解题的关键是根据摸到“兴文”球的频率稳定在左右进行求解即可．
【详解】设口袋中“兴文”球有x个，
根据题意，得：，
所以估计口袋中 “兴文”球有个．
故选：B
5. 下列计算正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】此题考查了二次根式的运算和特殊角的三角函数值，根据二次根式的运算法则计算后即可得到答案．
【详解】解：A．与不是同类二次根式，不能合并，故选项错误，不符合题意；
B．，故选项错误，不符合题意；
C．，故选正确，符合题意；
D．，故选项错误，不符合题意．
故选：C．
6. 如图，在平面直角坐标系中，已知点，，以坐标原点O为位似中心作一条线段，使该线段与线段AB的相似比为，正确的画法是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】此题考查作图-位似变换，解题关键是画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．根据题意分两种情况画出满足题意的线段，即可做出判断．
【详解】解：画出图形，如图所示：
故选D．
7. 一元二次方程的根的情况是（ ）
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 没有实数根D. 无法确定
【答案】A
【解析】
【分析】根据判别式的值确定根的情况即可．
【详解】解：，
∴有两个不相等实数根，
故选A．
【点睛】本题主要考查判别式与根的关系，能够熟练计算判别式并判断根的情况是解题关键．
8. 高空抛物极其危险，是我们必须杜绝的行为．据研究，高空抛物下落的时间（单位：s）和高度h（单位：m）近似满足公式（不考虑风速的影响）．记从高空抛物到落地所需时间为．从高空抛物到落地所需时间为，则的值是（ ）
A. B. C. D. 2
【答案】C
【解析】
【分析】将代入进行计算即可；将代入进行计算，再计算与的比值即可得出结论．
【详解】当时，（秒；
当时，（秒；
，
故选：C．
【点睛】本题主要考查了二次根式的应用，二次根式的应用主要是在解决实际问题的过程中用到有关二次根式的概念、性质和运算的方法．
9. 某品牌今年推出新品销售，1月份销售量为5万件，由于质量过硬，市场反馈良好，销售量逐月增加，一季度共销售万件，已知2、3两个月份销售量的月增长率相同．设2月份销售量的月增长率为x，则可列方程为（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】设2、3月份销售量的月增长率为x，则2月份的利润为，3月份的利润为，再根据一季度共销售万件，即可列出关于x的一元二次方程．
【详解】解：设2、3月份销售量的月增长率为x，则2月份的利润为，3月份的利润为，
由题意得：，
故选：D．
【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
10. 如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段，则线段的长是（ ）

A. B. 2C. D. 5
【答案】D
【解析】
【分析】过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在平行横线于E，根据平行线分线段成比例定理，列出比例式，计算即可得解．
【详解】解：过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在平行横线于E，

，
五线谱是由等距离的五条平行横线组成的，
，
，
解得，
故选：D．
【点睛】此题考查了平行线分线段成比例定理，熟练掌握并灵活运用该定理、找准对应线段是解答此题的关键．
11. 如图，在中，，、分别为、的中点，平分，交于点，若，，则的长为（ ）
A. 2B. 1C. 4D.
【答案】A
【解析】
【分析】根据勾股定理得到，根据三角形中位线定理得到，，根据平行线的性质得到，根据角平分线的定义得到，求得，得到，于是得到结论．
【详解】解：在中，，，，
，
、分别为、的中点，
是的中位线，
，，
，
平分，
，
，
，
，
故选：A．
【点睛】本题考查的是三角形中位线定理、勾股定理、平行线的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
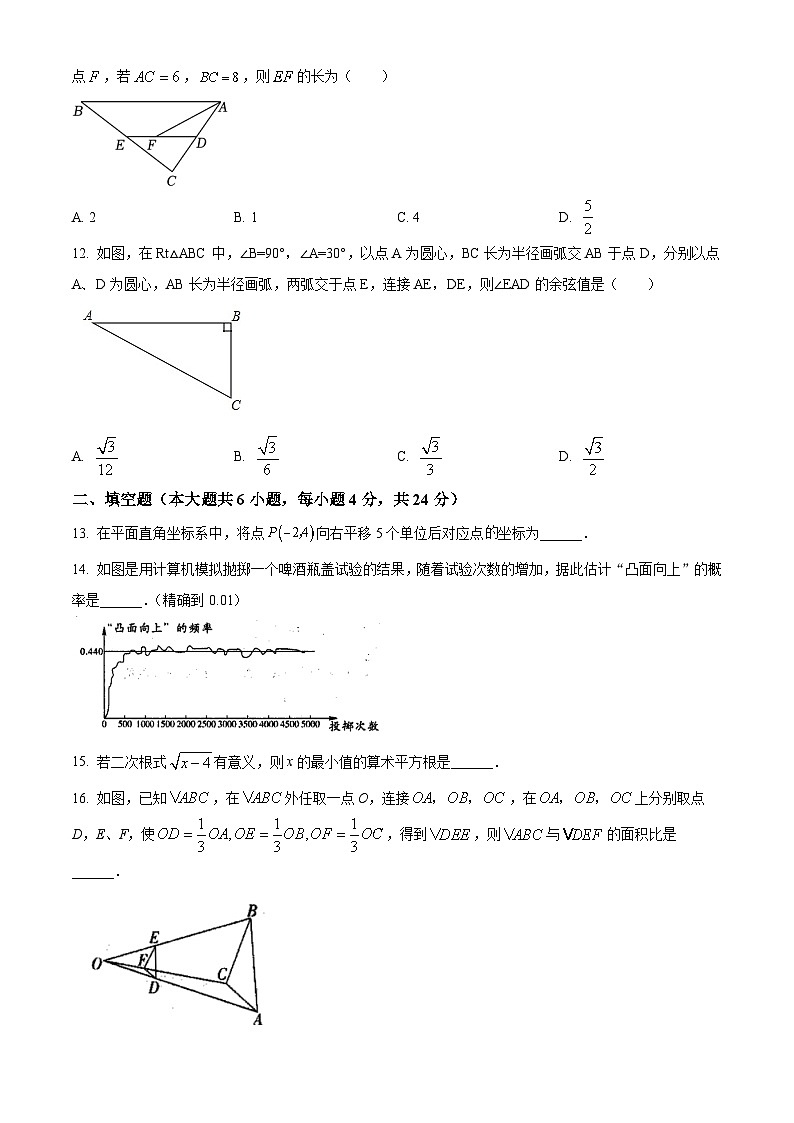
12. 如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ）
A. B. C. D.
【答案】B
【解析】
【详解】试题解析：如图所示：
设BC=x，
∵在Rt△ABC中，∠B=90°，∠A=30°，
∴AC=2BC=2x，AB=BC=x，
根据题意得：AD=BC=x，AE=DE=AB=x，
作EM⊥AD于M，则AM=AD=x，
在Rt△AEM中，cs∠EAD=；
故选B．
【点睛】本题考查了解直角三角形、含30°角的直角三角形的性质、等腰三角形的性质、三角函数等，通过作辅助线求出AM是解决问题的关键.
二、填空题（本大题共6小题，每小题4分，共24分）
13. 在平面直角坐标系中，将点向右平移5个单位后对应点的坐标为______．
【答案】
【解析】
【分析】此题主要考查对坐标与图形变化-平移的理解和掌握，能根据平移性质进行计算是解此题的关键．根据平移的性质得出所对应的点的横坐标是，纵坐标不变，求出即可．
【详解】解：∵在平面直角坐标系中，将点向右平移5个单位，
∴所对应的点的横坐标是，纵坐标不变，
∴所对应的点的坐标是，
故答案为：．
14. 如图是用计算机模拟抛掷一个啤酒瓶盖试验的结果，随着试验次数的增加，据此估计“凸面向上”的概率是______．（精确到0.01）
【答案】
【解析】
【分析】本题考查了模拟实验，由频率估计概率，解题的关键是明确概率的定义．根据图中的数据即可解答．
【详解】解：由图可知，随着试验次数的增加，“凸面向上”的频率逐渐稳定在附近，
“凸面向上”的概率为，
故答案为：．
15. 若二次根式有意义，则x的最小值的算术平方根是______．
【答案】2
【解析】
【分析】此题考查了二次根式有意义的条件、算术平方根、解一元一次不等式等知识，根据二次根式有意义的条件得到，求出不等式的解集，找到x的最小值求出其算术平方根即可．
【详解】解：若二次根式有意义，则，
解得，
∴x的最小值为4，
4的算术平方根是2，
故答案为：2
16. 如图，已知，在外任取一点O，连接，在上分别取点D，E、F，使，得到，则与的面积比是______．
【答案】
【解析】
【分析】此题考查了位似的性质，相似三角形的判定和性质，根据三边成比例的三角形相似得到，根据相似三角形的面积比等于相似比的平方即可得到答案．
【详解】解：∵，
∴，
∴，
∴与的面积比是，
即与的面积比是
故答案为：．
17. 如图，在中，，是的中线，E是的中点，连接．若，则的度数为______．

【答案】##30度
【解析】
【分析】本题考查了直角三角形斜边上的中线，勾股定理，熟练掌握直角三角形斜边上的中线性质是解题的关键．根据垂直定义可得，从而在中，利用直角三角形斜边上的中线性质可得，再在中，利用直角三角形斜边上的中线性质可得，从而可得是等边三角形，然后利用等边三角形的性质可得，从而利用直角三角形的两个锐角互余可得度数．
【详解】解：，
，
点是的中点，
，
，是的中点，
，
，
是等边三角形，
，
，
故答案为：．
18. 如图，四边形是边长为5的菱形，对角线，的长度分别是一元二次方程的两实数根，是边上的高，则________．

【答案】####
【解析】
【分析】根据菱形的性质得出，，，，求出，根据勾股定理得出，根据根与系数的关系得出，，变形后代入求出的值，即可得出答案．
【详解】解：四边形是菱形，
，，，，
，
，
对角线，的长度分别是一元二次方程的两实数根，
，，
，，
，
，
解得：，，
当时，，不符合题意，舍去，
即，
则，，
是边上的高，
，
，
．
故答案为：．
【点睛】本题考查了菱形的性质和面积，勾股定理，根与系数的关系的应用，能得出关于的方程是解此题的关键，注意：菱形的对角线互相平分且垂直．
三、解答题（本大题共7小题，共78分．解答时应写出必要的文字说明、证明过程或演算步骤）
19. （1）解方程：
（2）计算：．
【答案】（1），；（2）
【解析】
【分析】此题考查了解一元二次方程和二次根式的混合运算，熟练掌握因式分解法和二次根式的运算法则是解题的关键．
（1）利用因式分解法解方程即可；
（2）先计算二次根式的除法和利用完全平方公式展开，再进行加减法即可．
【详解】解：（1）
∴
∴，
则或，
解得，
（2）
20. 如图，已知，求证：．
【答案】见解析
【解析】
【分析】此题考查了相似三角形的判定和性质，根据三边成比例的两个三角形相似得到，则，即可得到，又由两边成比例且夹角相等的两个三角形相似得到．
【详解】证明：∵，
∴，
∴，
∴，
∴，
∵，
∴，
∴．
21. 实数a在数轴上的对应点的位置如图所示．
（1）化简：_______；______．
（2）若最简二次根式与是同类二次根式，求a的值．
【答案】（1），
（2）或．
【解析】
【分析】本题主要考查最简二次根 及二次根式的化简，数轴，解答的关键是对相应的知识的掌握．
（1）由数轴可得，再根据二次根式的性质进行求解即可；
（2）根据最简二次根式和同类二次根式的定义列方程求解即可．
【小问1详解】
由数轴得：，
，
．
故答案为：，；
【小问2详解】
解：最简二次根式与是同类二次根式，
，
解得：或．
22. 为了培养同学们的创新精神和实践能力，宜宾市某校组织学生开展了为期一周的社会实践活动．每位同学可以在“篮球韵律操”“苗族银饰雕刻”“酿酒”“摄影”四门实践课程中选择一门．为公平起见，学校制作了如图所示的转盘，转盘被分成了四等份，学生转动转盘一次，指针指到的课程即自己参加的实践课程（当指针指到分界线上时，则重转）．
（1）若小明是该校的一名学生，他参加“酿酒”实践课程是______事件（填“不可能”“必然”或“随机”），参加“酿酒”实践课程的概率是______；
（2）同校小亮是小明的好朋友，他们想参加相同的实践课程，请用列表法或画树状图法求出小明和小亮同时参加“篮球韵律操”实践课程的概率．
【答案】（1）随机，
（2）
【解析】
【分析】本题考查列表法或树状图法，列举出所有等可能出现的结果是正确解答的前提，理解概率的定义是解决问题的关键．
（1）根据随机事件，必然事件、不可能事件的意义结合具体问题情境进行判断即可；
（2）用列表法表示小明、小亮所有选择可能出现的结果，再根据概率公式进行计算即可．
【小问1详解】
解：小明是该校的一名学生，他参加“酿酒”实践课程是随机事件，由于转盘被分成了四等份，学生转动转盘一次，指针指到的课程即自己参加的实践课程（当指针指到分界线上时，则重转），
∴参加“酿酒”实践课程的概率是，
故答案为：随机，；
【小问2详解】
解：设“篮球韵律操”“苗族银饰雕刻”“酿酒”“摄影”四门实践课程分别用A、B、C、D表示，用列表法表示小明、小亮所有等可能出现的结果如下：
共有16种等可能出现的结果，其中，小明、小亮同时参加“篮球韵律操”实践课程的情况有1种，
所以小明、小亮同时参加“篮球韵律操”实践课程的概率为．
23. 某社区在开展“美化社区，幸福家园”活动中，计划利用如图所示的直角墙角（阴影部分，两边足够长），用50米长的篱笆围成一个矩形花园（篱笆只围，两边）．

（1）若花园的面积为400米2，求的长；
（2）若在直角墙角内点处有一棵桂花树，且与墙，的距离分别是10米，30米，要将这棵树围在矩形花园内（含边界，不考虑树的粗细），则花园的面积能否为625米2？若能，求出的值；若不能，请说明理由．
【答案】（1）10米或40米
（2）不能，见解析
【解析】
【分析】（1）设的长为米，则的长为米，由矩形的面积公式列出方程，解方程即可得到答案；
（2）设的长为米，则的长为米，由矩形的面积公式列出方程，解方程即可得到答案．
【小问1详解】
解：设的长为米，则的长为米，
由题意得：，
解得：，
即的长为10米或40米；
【小问2详解】
解：花园的面积不能为625米2，
理由如下：
设的长为米，则的长为米，
由题意得：
，
解得：，
当时，，
即当米，米30米，
∴花园的面积不能为625米2．
【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
24. 如图，在岷江的右岸边有一高楼，左岸边有一坡度的山坡，点C、B在同一水平面上，与在同一平面内；某数学兴趣小组为了测量楼的高度，在坡底C处测得楼顶A的仰角为，然后沿坡面上行了到达D处，此时在D处测得楼顶A的仰角为，求楼的高度．（结果精确到；参考数据：，，，）
【答案】楼的高度为米
【解析】
【分析】由，，解得，，过点D作于G，过点C作于H，则四边形、四边形、四边形都是矩形，证得，设，则，，在中，，代入即可得出结果．
【详解】
如图，过点D作于G，过点C作于H，
则四边形、四边形、四边形都是矩形，
在中，
，，，
∴，
解得：，
，
，，
，
设，则，，
在中，
，
，
解得：，
经检验，是方程的解．
答：楼的高度为米．
【点睛】本题考查了解直角三角形的应用﹣方向角问题，通过解直角三角形得出方程是解题的关键．
25. 如图，在矩形中，，为边的中点，为对角线的中点，以点为顶点作，交边于点，交边于点，连接．
（1）求的值；
（2）求证：；
（3）作射线与射线交于点，若，，求的长．
【答案】（1）
（2）见解析 （3）
【解析】
【分析】本题考查了矩形性质，相似三角形的判定与性质，解题的关键是添加辅助线，构造相似三角形．
（1）取的中点，连接，，只要证明，可得；
（2）利用相似三角形的性质即可解决问题；
（3）延长交于．由，，设，，，，由，可推出，可得，，，，在，根据勾股定理可得，解得，推出，，，根据，可得，设，根据，， DH∥BE，由此构建方程即可．
【小问1详解】
取的中点，连接，，
，，，
，，，，
四边形是平行四边形，
，
四边形是矩形，
，
，
，
，
；
【小问2详解】
证明：，
，
，
，
，
是的中点，
，
；
【小问3详解】
延长交于，
，，设，，，，
，即，
，
，
，，，，
在中，，
，
解得：，
，，，
，
，可得，设，
，
，
，
，
．
A
B
C
D
A
B
C
D