浙教版2023-2024学年八年级上册数学期末复习卷(1)及答案

这是一份浙教版2023-2024学年八年级上册数学期末复习卷(1)及答案，共9页。试卷主要包含了在平面直角坐标系中，点在，若，则下列式子中错误的是，函数中自变量的取值范围是等内容，欢迎下载使用。

1．下列长度的三条线段，能组成三角形的是
A．1，2，3B．4，5，10C．7，8，9D．9，10，20
2．在平面直角坐标系中，点在
A．第一象限B．第二象限C．第三象限D．第四象限
3．下列各图中，正确画出边上的高的是
4．若，则下列式子中错误的是
A．B．C．D．
5．在平面直角坐标系中，点与点关于轴对称，则点的坐标为
A．B．C．D．
6．函数中自变量的取值范围是
A．B．C．D．
7．能说明命题“对于任何实数，”是假命题的一个反例可以是
A．B．C．D．
8．如图，直线为常数，经过点，若是该直线上一点，则点的坐标可能是
A．B．C．D．
9．直角三角形的两条边长分别是5和12，则斜边上的中线长是
A．6B．6.5C．6或6.5D．6或2.5
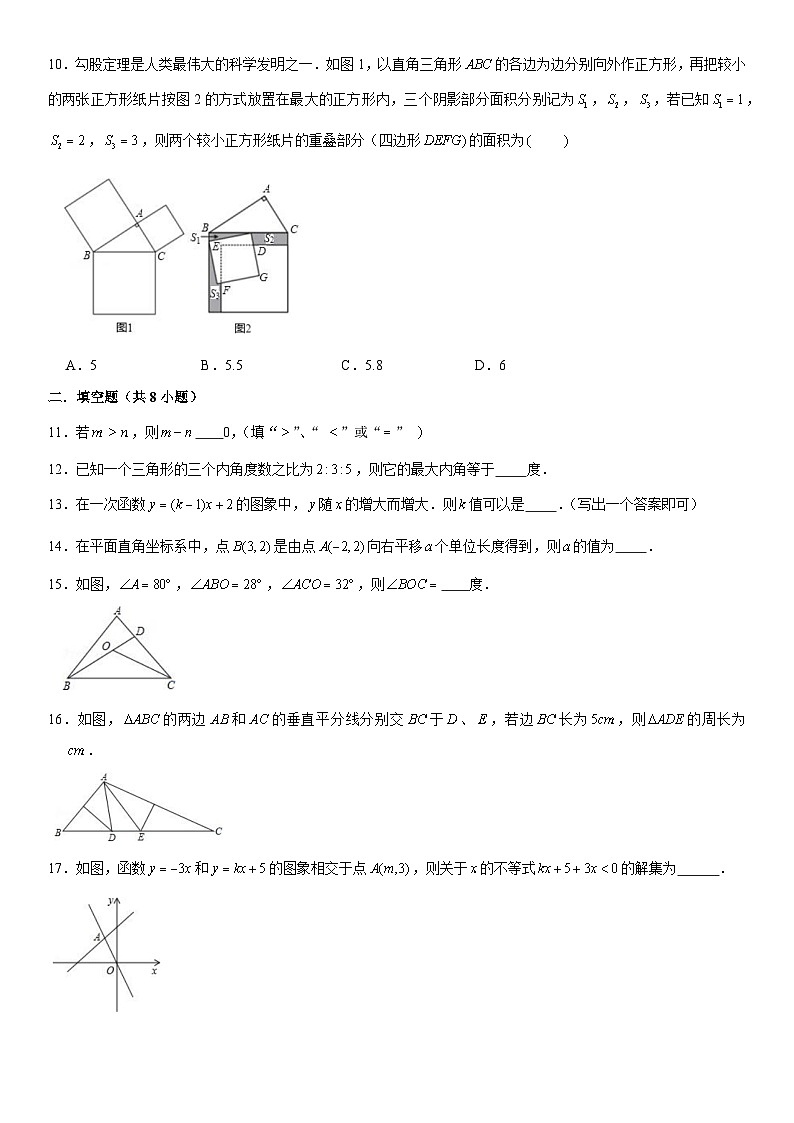
10．勾股定理是人类最伟大的科学发明之一．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，三个阴影部分面积分别记为，，，若已知，，，则两个较小正方形纸片的重叠部分（四边形的面积为
A．5B．5.5C．5.8D．6
二．填空题（共8小题）
11．若，则 0，（填“”、“ ”或“”
12．已知一个三角形的三个内角度数之比为，则它的最大内角等于 度．
13．在一次函数的图象中，随的增大而增大．则值可以是 ．（写出一个答案即可）
14．在平面直角坐标系中，点是由点向右平移个单位长度得到，则的值为 ．
15．如图，，，，则 度．
16．如图，的两边和的垂直平分线分别交于、，若边长为，则的周长为 ．
17．如图，函数和的图象相交于点，则关于的不等式的解集为 ．
18．在平面直角坐标系中，已知点，，，在直线BC上找一点P，使得∠BAP=∠ABO，请写出所有满足条件的点P的坐标 ．
三．解答题（共7小题）
19．如图，是线段的垂直平分线，则,请说明理由.
20．解不等式组
（1）
，并把解集在数轴上表示出来．
21．如图，在方格纸中，每一个小正方形的边长为1，按要求画一个三角形，使它的顶点都在小方格的顶点上．
（1）在图甲中画一个以为边且面积为3的直角三角形．
（2）在图乙中画一个以为腰的等腰三角形．
22．如图，在等边三角形中，是上的一点，是延长线上一点，连接，，已知．
（1）求证：是等腰三角形．
（2）当，时，求的长．
23．，两地相距200千米．早上货车甲从地出发将一批物资运往地，行驶一段路程后出现故障，即刻停车与地联系．地收到消息后立即派货车乙从地出发去接运甲车上的物资．货车乙遇到甲后，用了18分钟将物资从货车甲搬运到货车乙上，随后开往地．两辆货车离开各自出发地的路程（千米）与时间（小时）的函数关系如图所示．（通话等其他时间忽略不计）
（1）则货车甲出发时的速度是 千米/小时，则货车乙的速度是 千米/小时.
（2）求货车乙在整个过程中，直接写出路程关于的函数表达式，并写出相应自变量的取值范围.
24．在平面直角坐标系中，已知点，，若在坐标轴上存在点，使得，则称点为点，的“的和谐点”．例如坐标为时，，则称为点，的“6的和谐点”．
（1）若点为点，的“的和谐点”，且为等腰直角三角形，求的值；
（2），的“10的和谐点”有几个，请分别求出左边;
（3）直接指出，的“的和谐点”的个数情况和相应的取值条件．
参考答案
一．选择题（共10小题）
1．选：．
2．选：．
3．选：．
4．选：．
5．选：．
6．选：．
7．选：．
8．选：．
9．选：．
10．选：．
二．填空题（共8小题）
11．答案为：．
12．答案为：90．
13．答案为：2．
14．答案为：5．
15．答案为：140.
16．答案为：5．
17．答案为：．
18．答案为：，．
三．解答题（共7小题）
19．【解答】解：
是线段的垂直平分线，，（线段垂直平分线上的点到线段两端的距离相等），
在和中，
（公共边）
和，
（全等三角形的对应角相等）．
20．【解答】解：（1）；
（2）；
在数轴上表示为：
21．【解答】解：（1）如图甲中，即为所求．
（2）如图乙中，即为所求．
22．【解答】（1）证明：是等边三角形，
，
，，，
，
，
是等腰三角形；
（2）解：设，则，
，
，
，
，
，
过作于，
，，
，，，
．
23．【解答】解：（1）
50,80
（2）设函数表达式为，
把，代入，得，
解得：，
关于的函数表达式为；
同理可得：关于的函数表达式为；
24．【解答】解：（1）点，，
，
为等腰直角三角形，
，
,即；
（2）设点是点，的“10的和谐点”，分类讨论：
①如果点在轴上，设点坐标为.
，
，
当时，，解得，所以点坐标为；
当时，，无解；
当时，，解得，所以点坐标为；
②如果点在轴上，设点坐标为.
.
，
，
所以点坐标为；
综上所述，，的“10的和谐点”有4个，坐标为，，；
（3），
点，的“的和谐点”的个数情况分三种情况：
当时，，的“的和谐点”没有；
当时，，的“的和谐点”有无数个；
③当时，，的“的和谐点”有个.