备战2024年高考数学模拟卷（新题型地区专用03）试卷（Word版附解析）

这是一份备战2024年高考数学模拟卷（新题型地区专用03）试卷（Word版附解析），文件包含黄金卷032024新题型备战2024年高考数学模拟卷新题型地区专用Word版含解析docx、黄金卷032024新题型备战2024年高考数学模拟卷新题型地区专用参考答案docx、黄金卷032024新题型备战2024年高考数学模拟卷新题型地区专用考试版docx等3份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
（考试时间：120分钟 试卷满分：150分）
第I卷（选择题）
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．
9．AD10．AC11．ACD
三、填空题：本题共3小题，每小题5分，共15分．
12．13．4414．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（13分）
【答案】（1）；（2）
【解析】（1）因为，
所以，
令，则有，分
当时，单调递减，当时，单调递增，
因此当时，则有，
因此当时，则有，分
当时， 显然，
于是有当时，函数单调递减，当时，函数单调递增，
所以；分
（2）由，
因为在上单调递减，
所以在上恒成立，分
由，
设，则有，
当时，单调递减，
当时，单调递增，
所以，分
要想在上恒成立，
只需，因此的取值范围为分
16．（15分）
【答案】（1）；（2）分布列见解析，
【解析】（1）由题意知共有个团队，
一次抽取2个团队的情况有种，其中全是私家游团队的情况有种，
故一次抽取2个团队，全是私家游团队的概率是，
整理得，解得或（舍去），分
若一次抽取的3个团队全是私家游团队，则共有种情况，
若一次抽取的3个团队全是跟团游团队，则共有种情况，
所以在抽取的3个团队是同类型团队的条件下，
这3个团队全是跟团游团队的概率为；分
（2）由题意知，随机变量的所有可能取值为0，1，2，3，4，分
，，
，，
，分
故的分布列为
数学期望分
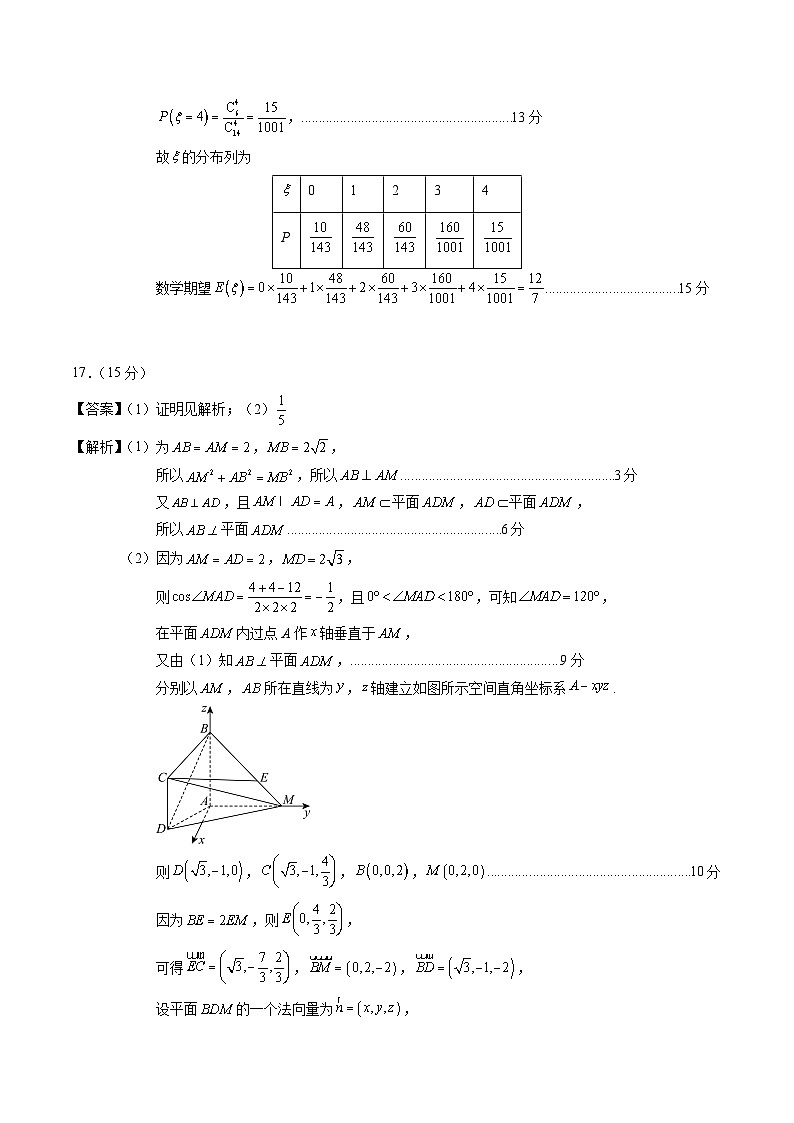
17．（15分）
【答案】（1）证明见解析；（2）
【解析】（1）为，，
所以，所以分
又，且，平面，平面，
所以平面分
（2）因为，，
则，且，可知，
在平面内过点A作轴垂直于，
又由（1）知平面，分
分别以，所在直线为，轴建立如图所示空间直角坐标系.
则，，，分
因为，则，
可得，，，
设平面的一个法向量为，
则，取得，分
设直线与平面所成角为，
则，
所以直线与平面所成角的正弦值为分
18．（17分）
【答案】（1）；（2）证明见解析
【解析】（1）（1）设，
因为点N在曲线上，所以，分
因为，所以，分
代入可得，
即，即的方程为；分
（2）因为以为直径的圆经过点O，所以，
当C、D为椭圆顶点时，分
当C、D不是椭圆顶点时，可得直线OC的斜率存在且不等于零，
可设直线OC的方程为，则直线OD的方程为，
由，得，
所以分
同理可得，，，分
所以
综上，为定值分
19．（17分）
【答案】（1）、；（2）证明见解析；（3）或
【解析】（1）由“数列”的定义可知，数列、为“数列”. 分
（2）证明：若，则由①可知，
所以或，且公差，分
以下设.
由①，、，，，
两式作差得，
因为，所以.
由①，、，，，
两式作差得，
因为，所以，因此，分
若，则等差数列是递减数列，
由①为中的项，因此，，解得，
由且公差，所以或，，，
由①，为中的项，且，
这与等差数列递减矛盾，因此，不成立.
综上，且公差分
（3）因为公差，所以，即是递增数列.
若，因为，所以，
则，且，
由①为中的项，这与等差数列是递增数列矛盾.
因此，，分
又由（2），故.
由，知，且中存在一项为正整数，取最小的正整数项.
则由②，，使得且，.
因此，解得，
又，故分
因为是递增数列，
（i）若，则，此时.
因为，，
令，有，且，所以满足条件①.
因为，
令，有，所以满足条件②. 分
（ii）若，则，.
因为，
.
令，则，且，所以满足条件①.
因为，令，，有，所以满足条件②.1
2
3
4
5
6
7
8
B
A
C
D
C
A
D
B
0
1
2
3
4
P