云南省玉溪市红塔区2023年中考模拟数学考试试卷

这是一份云南省玉溪市红塔区2023年中考模拟数学考试试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，共36分。在每小题列出的选项中，选出符合题目的一项）
1．甲地的海拔高度是−3米，乙地的海拔高度是12米，则甲地的海拔高度比乙地的海拔高度低（ ）
A．9米B．−9米C．15米D．−15米
2．下列几何体中，主视图(主视图也称正视图)和俯视图形状不相同的是（ ）
A．B．
C．D．
3．六边形的内角和为（ ）
A．360°B．540°C．720°D．900°
4．函数y=2−xx−1中，自变量x的取值范围是（ ）
A．x≤2B．x≤2且x≠1C．x≥2D．x≥1
5．一元二次方程x2+2=x的根的情况是（ ）
A．没有实数根B．有两个不相等的实数根
C．有两个相等的实数根D．有一个实数根
6．已知等腰三角形的周长为20，一边长为4，则这个等腰三角形的底边长为（ ）
A．4B．8C．12D．4或12
7．已知反比例函数y=kx(k≠0)的图象经过点(3，−3)，那么该反比例函数的图象也一定经过点（ ）
A．(−1，−9)B．(9，1)C．(−3，1)D．(−3，3)
8．按一定规律排列的单项式：x2，2x4，4x6，8x8，16x10，32x12，…，第n个单项式是（ ）
A．2nx2nB．2n−1x2nC．(2n−2)x2nD．n2x2n
9．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是AD的中点，连接OE.若△AOE的面积为5，则平行四边形ABCD的面积为（ ）
A．10B．20C．40D．80
10． 下列说法正确的是（ ）
A．调查红塔区中小学生的视力情况，应该采用全面调查的方式
B．一组数据2，0，2，3，2，1的众数和平均数都是2
C．抛掷一枚质地均匀的硬币1000次，一定有500次正面向上
D．甲、乙两个班级参加体育艺术节的开幕式，若甲、乙两个班级学生身高的平均数相同，方差分别是S甲2=0.41，S乙2=2.9，则甲班级学生的身高较乙班级学生的身高更整齐
11．将一个直角三角形以一条直角边所在的直线为轴旋转一周，得到一个圆锥，若这个直角三角形斜边的长为13cm，圆锥的侧面积为65πcm2，则该圆锥的高为（ ）
A．5cmB．12cmC．13cmD．69cm
12．若关于x的不等式组3−(x−1)≥25x−a>4x有且只有3个整数解，则a的取值范围是（ ）
A．−1≤a<0B．−1二、填空题（本大题共4小题，共8分）
13． 云南加快建设我国面向南亚东南亚辐射中心，云南至南亚东南亚国家通航城市最多达43个，数量居全国第一，基本实现南亚东南亚首都和重要旅游城市航线全覆盖.中老铁路黄金线路效应持续扩大，一年多来，中老铁路发送旅客突破10450000万人次，累计运输货物1450.47万吨.用科学记数法可以把数字10450000表示为 ．
14．如图，直线l与直线a，b相交，且a//b，∠1=70°，则∠2的度数是 度．
15． 分解因式：ax2−25a= ．
16．点B是以AC为直径的⊙O上的一点，tan∠BAC=33，AC=43，点D是直线AB上一点，且∠BCD=30°，则线段AD的长为 ．
三、解答题（本大题共8小题，共56分。解答应写出文字说明，证明过程或演算步骤）
17． 计算：(−2)2−4sin45°−(12)−1+8−(π−2023)0．
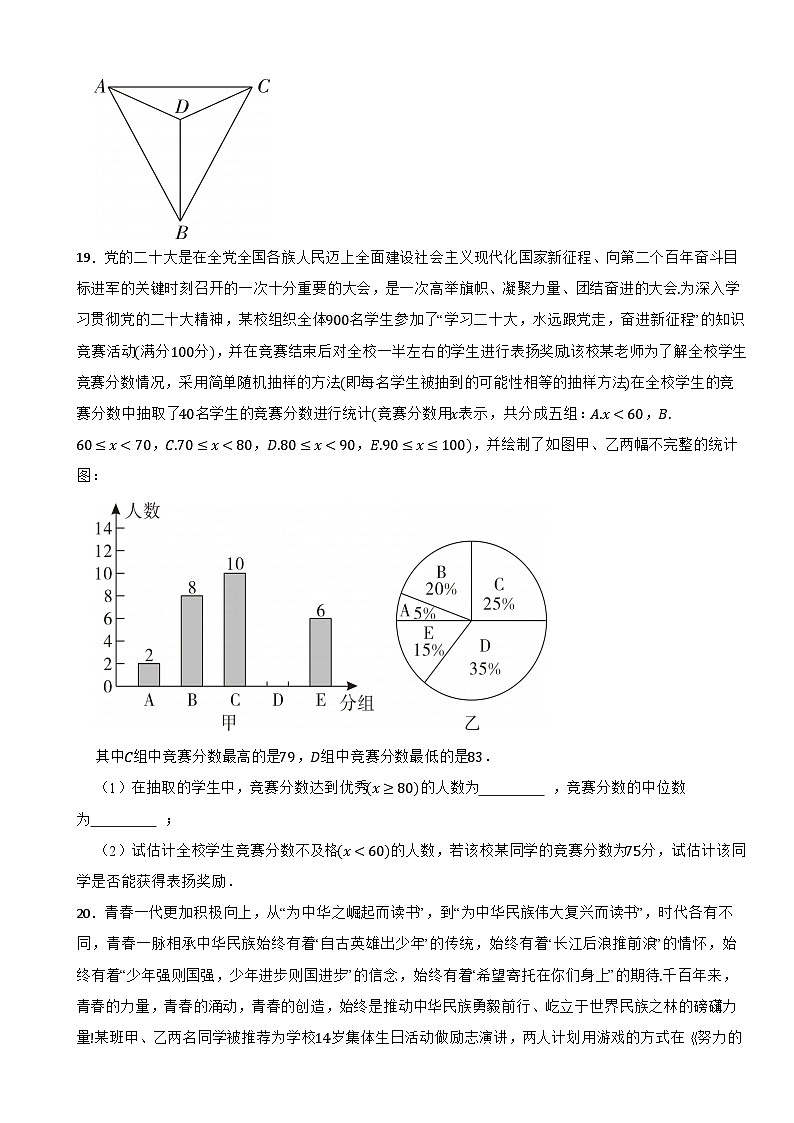
18．如图3，点D是△ABC内部一点，连接AD，BD，CD，∠DAC=∠DCA，∠ADB=∠CDB
求证：BD平分∠ABC．
19．党的二十大是在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会，是一次高举旗帜、凝聚力量、团结奋进的大会.为深入学习贯彻党的二十大精神，某校组织全体900名学生参加了“学习二十大，水远跟党走，奋进新征程”的知识竞赛活动(满分100分)，并在竞赛结束后对全校一半左右的学生进行表扬奖励.该校某老师为了解全校学生竞赛分数情况，采用简单随机抽样的方法(即每名学生被抽到的可能性相等的抽样方法)在全校学生的竞赛分数中抽取了40名学生的竞赛分数进行统计(竞赛分数用x表示，共分成五组：A.x<60，B.60≤x<70，C.70≤x<80，D.80≤x<90，E.90≤x≤100)，并绘制了如图甲、乙两幅不完整的统计图：
其中C组中竞赛分数最高的是79，D组中竞赛分数最低的是83．
（1）在抽取的学生中，竞赛分数达到优秀(x≥80)的人数为 ，竞赛分数的中位数为 ；
（2）试估计全校学生竞赛分数不及格(x<60)的人数，若该校某同学的竞赛分数为75分，试估计该同学是否能获得表扬奖励．
20．青春一代更加积极向上，从“为中华之崛起而读书”，到“为中华民族伟大复兴而读书”，时代各有不同，青春一脉相承.中华民族始终有着“自古英雄出少年”的传统，始终有着“长江后浪推前浪”的情怀，始终有着“少年强则国强，少年进步则国进步”的信念，始终有着“希望寄托在你们身上”的期待.千百年来，青春的力量，青春的涌动，青春的创造，始终是推动中华民族勇毅前行、屹立于世界民族之林的磅礴力量!某班甲、乙两名同学被推荐为学校14岁集体生日活动做励志演讲，两人计划用游戏的方式在《努力的我们最美丽》与《青春的呐喊》中确定一个题目作为本次演讲的题目.游戏规则如下，在一个不透明的口袋中装有标号分别为1，2，3的三张卡片(除标号外，其余都相同)，甲从口袋中任意摸出1张卡片，记卡片上的标号为a，并将卡片放回口袋中，充分摇匀后，乙从口袋中任意摸出1张卡片，记卡片上的标号为b.若甲、乙取出的卡片标号相同，则演讲的题目为《青春的呐喊》；否则，演讲的题目为《努力的我们最美丽》．
（1）用列表法或树状图法(树状图也称树形图)中的一种方法，写出(a，b)所有可能出现的结果总数；
（2）求演讲的题目为《努力的我们最美丽》的概率P．
21． 如图，在△OAB中，点C是AB边上一点，以点O为圆心，OC为半径作⊙O，交OB于点D，交OA于点E，连接CD，∠COD=2∠BCD．
（1）试判断AB与⊙O的位置关系，并证明你的结论；
（2）若∠AOB=90°，OA=3，OB=4，求图中阴影部分的面积．
22． 云南玉溪米线文化节是玉溪各族人民的传统节日，自每年正月初一起，至三月二十二日止，历时81天，创世界纪录协会世界上历时最长的节日世界纪录.“小锅米线凉米线，各具风味有特色.鳞鱼米线辣味汤，五味齐全又一色.过桥米线斗大碗，油汤飘香藏典故.土鸡米线大小碗，碗中包含玉溪情.玉溪米线吃齐全，不枉登陆玉溪城”米线节期间，某店铺购进A，B两种米线进行销售.若购进1斤A种米线和2斤B种米线共需花费4元，购进3斤A种米线和4斤B种米线共需花费9元.已知该店A，B两种米线的售价如下表：
经过市场调查，该店计划在米线节期间每天售出米线共200斤，且每天售出A种米线的数量不少于B种米线的3倍，设该店在米线节期间每天售出A种米线x斤，米线节期间共计81天的总利润为y元．
（1）求购进每斤A种米线、B种米线的价格分别是多少元？
（2）x取何值时，总利润y最大？并求出最大总利润．
23． 如图，四边形ABCD是矩形，AC和BD相交于点O，过点C作CE//BD，且CE=12AC，连接DE.点P是线段CD上与点C，点D不重合的一个动点，过点P分别作CE，DE的垂线，垂足分别为点F，点G．
（1）求证：四边形OCED是菱形；
（2）若BC=2AB，则在点P的运动中，ACCF+DG的值是否会发生变化？若不变化，求出其值；若变化，请说明理由．
24． 已知经过点(0，−12)的抛物线y=12x2+22x+c与x轴分别交于点A(r，0)和点B(s，0)，点A到点B的距离为d，M=r9s3+r5s5−12r5s3+r5s+rs32r5s3−r6s2−r4s4．
（1）求c，d的值；
（2）@试比较M的值与1的大小，并说明理由．
答案解析部分
1．【答案】C
【知识点】有理数及其分类
【解析】【解答】 甲地的海拔高度比乙地的海拔高度低 =乙地的海拔高度-甲地的海拔高度=12-（-3）=15米；
故答案为：C.
【分析】用乙地的海拔高度减去甲地的海拔高度即可得出答案.
2．【答案】D
【知识点】简单几何体的三视图
【解析】【解答】D选项的主视图，俯视图，所以 主视图和俯视图形状不相同。
故答案为：D。
【分析】由每个图像从前面看得到主视图，从上面看得到俯视图，从而可确定答案。
3．【答案】C
【知识点】多边形内角与外角
【解析】【解答】解：根据多边形的内角和可得：
（6﹣2）×180°=720°．
故答案为：C．
【分析】由多边形内角和公式（n﹣2）×180°可解答。
4．【答案】B
【知识点】函数自变量的取值范围
【解析】【解答】解2−x≥0得x≤2，
解x−1≠0的x≠1，
所以x的取值范围为x≤2且x≠1.
故答案为：B.
【分析】由二次根式的非负性和分母不为零即可得出结果。
5．【答案】A
【知识点】一元二次方程根的判别式及应用
【解析】【解答】△=b2−4ac=02−4×1×2=−8<0，所以原方程没有实数根，
故答案为：A.
【分析】由一元二次方程判根公式△=b2−4ac，△>0有不相等的两个实数根；△=0有相等的两个实数根；△<0没有实数根，从而确定答案。
6．【答案】A
【知识点】三角形三边关系；等腰三角形的性质
【解析】【解答】1.当底边为4时，腰为20−4÷2=8，三边分别为8、8、4，可以构成三角形；
2.当腰为4时，底边为20−2×4=12，三边分别为4、4、12，构不成三角形；
综上所述，底边为4.
故答案为：A.
【分析】由三角形的三边之间的关系确定是否构成三角形，来确定底边的长度。
7．【答案】D
【知识点】反比例函数的图象；待定系数法求反比例函数解析式
【解析】【解答】将点（3，-3）代入y=kxk≠0中，得k=-9，所以反比例函数为y=−9xk≠0；
A.将x=-1代入得y=9，所以A点不经过反比例函数；
B.将x=9代入得y=-1，所以B点不经过反比例函数；
C.将x=-3代入得y=3，所以C点不经过反比例函数；
D.将x=-3代入得y=3，所以D点经过反比例函数.
故答案为：D.
【分析】首先用待定系数法求出反比例函数函数的解析式，然后用代入法确定正确答案。
8．【答案】B
【知识点】探索数与式的规律
【解析】【解答】 系数1=20，2=21，4=22，8=23，16=24，32 =25… …，第n个单项式的系数为2n-1 ；
x2=x2×1，x4=x2×2，x6=x2×3，x8=x2×4，x10=x2×5，x12=x2×6… …，第n个式子为 x2n；
综上所述，第n个单项式为2n−1x2n.
故答案为：B.
【分析】 根据系数和式子的规律分别找出第n个单项式的系数和式子，最后组合求出第n个单项式。
9．【答案】C
【知识点】三角形的面积；平行四边形的性质；平行四边形的面积
【解析】【解答】∵点E是AD的中点，
∴S△ODE=S△AOE=5，
∴S△AOD=10，
∵AC，BD是平行四边形ABCD的中线，
∴S△AOD=S△AOB=S△COD=S△BOC=10，
∴平行四边形ABCD面积为40.
故答案为：C.
【分析】等底等高的三角形面积相等，由此可以求出S△AOE，同理可求出其他三角形的面积，即可得出平行四边形的面积。
10．【答案】D
【知识点】概率公式；方差；众数
【解析】【解答】A. 调查红塔区中小学生的视力情况，应该采用抽样调查的方式，故A错误 ；
B.众数为2，平均数为53，故B错误；
C. 抛掷一枚质地均匀的硬币1000次，正面向上的次数在500次左右，故C错误 ；
D.平均数相同时，方差越小则成绩越稳定，故D正确.
故答案为：D.
【分析】A.利用抽样调查和全面调查的适用范围即可确定A错误；
B.求出平均数和众数即可知B错误；
C. 抛掷硬币的概率为12代表的是每次抛掷是都有一半的可能是正面，并不是一定是一半的次数是正面，所以C错误；
D.由平均数相同时，方差越小则数据越稳定确定D正确.
11．【答案】B
【知识点】勾股定理；圆锥的计算
【解析】【解答】扇形的面积=12cl，12c×13=65π，解得c=10π，即圆锥的底面周长为10π，由C=2πr可得圆锥的半径即直角三角形的一直角边为5，由勾股定理可知x2+52=132，可知直角三角形的另一直角边为12，即圆锥的高为12.
故答案为：B.
【分析】由扇形的面积可求出地面圆的周长，进而求出底面圆的半径即直角三角形的一条直角边，再由勾股定理即可求出另一直角边即圆锥的高。
12．【答案】A
【知识点】一元一次不等式组的特殊解
【解析】【解答】解3−x−1≥2得x≤2，
解5x−a＞4x得x＞a，
因为该不等式组有且只有3个整数解，所以a所以−1≤a<0，
故答案为：A.
【分析】首先分别解出两个不等式的解，可知a13．【答案】1.045×107
【知识点】科学记数法表示大于10的数
【解析】【解答】10450000=1.045×107.
故答案为：1.045×107.
【分析】科学记数法a×10n1≤a＜10，从10450000的右往左数到1.045的小数位数为7，即可得出答案。
14．【答案】70
【知识点】平行线的判定与性质
【解析】【解答】如图，∵a//b
∴∠3=∠1=70°，
∴∠2=∠3=70°
故答案为：70。
【分析】两直线平行同位角相等，即可得到∠3=70°，∠2和∠3为对顶角，所以可得∠2=∠3=70°。
15．【答案】a(x+5)(x−5)
【知识点】因式分解﹣综合运用提公因式与公式法
【解析】【解答】解：原式=ax2−52=ax+5x−5，
故答案为ax+5x−5.
【分析】首先提公因式a，再利用平方差公式即可解得答案。
16．【答案】4或8
【知识点】特殊角的三角函数值；解直角三角形
【解析】【解答】解：∵tan∠BAC=33，
∴∠BAC=30°，
∵AC为⊙O的直径，
∴∠ABC=90°，
∴∠ACB=60°，
∵AC=43，
∴BC=12AC=23，
AB=cs30°⋅AB=32×43=6，
∵∠BCD=30°，
在Rt△BCD中，BD=tan30°⋅BC=33×23=2，
∴BD'=2，
当点D在△ABC内部时，AD=AB−BD=6−2=4，
当点D在△ABC外部时，AD'=AB+BD'=6+2=8，
综上所述，AD的长为4或8．
故答案为：4或8．
【分析】由tan∠BAC=33可知∠BAC=30°，从而可以求出BC；由∠BCD=30°，利用直角三角形中三角函数就可求出AD的长度，但是要注意D可以在AB之间，也可以在AB外，所以要分为两种情况进行计算即可。
17．【答案】解：(−2)2−4sin45°−(12)−1+8−(π−2023)0
=4−4×22−2+22−1
=4−22−2+22−1
=1．
【知识点】二次根式的混合运算；特殊角的三角函数值
【解析】【分析】由实数的乘方，三角函数中特殊角的值，以及二次根式的化简来计算即可。
18．【答案】证明：∵∠DAC=∠DCA，
∴AD=CD，
在△ABD与△CDB中，
AD=CD∠ADB=∠CDBBD=BD，
∴△ABD≌△CDB(SAS)，
∴∠ABD=∠CBD，
∴BD平分∠ABC．
【知识点】全等三角形的应用
【解析】【分析】在△ADC中，由等角对等边可知AD=CD，从而易证明△ABD≅△CBD，由对应角相等即可得到BD平分∠ABC。
19．【答案】（1）20；81
（2）解：900×5%=45(人)，
所以估计全校学生竞赛分数不及格(x<60)的人数大约为45人；
某同学的竞赛分数为75分，小于样本中位数，所以估计该同学不能获得表扬奖励．
【知识点】扇形统计图；条形统计图；利用统计图表分析实际问题
【解析】【解答】解：（1） 竞赛分数达到优秀的人数为 40×（35％+15％）=20人；
中位数为由低到高第20和21的分数的平均数即（79+83）2=81；
故（1）的第一空20人，第二空81；
（2）900×5％=45人；
某同学的竞赛分数为75分，小于样本中位数，所以估计该同学不能获得表扬奖励．
故（2）的答案为45人；不能获得表扬奖励。
【分析】（1）分数达到优秀的是D组和E组，即可求出分数达到优秀的人数；由中位数定义即可确定第20和21的分数的平均数，其中C组中竞赛分数最高的是79，D组中竞赛分数最低的是83，即是第20和21的分数。
（2） 全校学生竞赛分数不及格的即求总人数的5％；
奖励是对全校一半左右的学生进行表扬奖励 ，即是大于中位数的获奖，75分小于中位数，所以不能获奖。
20．【答案】（1）解：画树状图如下：
共有9种等可能的结果，即(1，1)、(1，2)、(1，3)、(2，1)、(2，2)、(2，3)、(3，1)、(3，2)、(3，3)；
（2）解：由(1)可知，共有9种等可能的结果，其中甲、乙取出的卡片标号不相同的结果有6种，
∴演讲的题目为《努力的我们最美丽》的概率P=69=23．
【知识点】列表法与树状图法
【解析】【分析】（1）由甲抽一次可知a可以是1，2，3中的一个，即分为三种情况；乙抽一次可知b也可以是1，2，3中的一个，即分为三种情况，所以总的可能是9种，按树状图画法画出即可；
（2）若a，b不相同就演讲《努力的我们最美丽》，从（1）的树状图结果中找出数字不同的即可得出结果。
21．【答案】（1）解：AB是⊙O的切线，理由：
证明：设∠BCD=x，则∠COD=2x，
∵OC=OD，
∴∠OCD=∠ODC=180°2x2=90°−x，
∴∠OCB=∠OCD+∠BCD=90°−x+x=90°，
∴OC⊥AB，
∵OC是⊙O半径，
∴AB是⊙O的切线；
（2）解：∵AOB=90°，
∴AB=OA2+OB2=32+42=5，
∵OC⊥AB，
∴OA⋅OB=AB⋅OC，
∴OC=125，
∴S阴影=S△AOB−S扇形OED，
=12×3×4−90π×(125)2360，
=6−3625π．
【知识点】勾股定理的应用；切线的判定与性质
【解析】【分析】（1）AB是 ⊙O 的切线，因为OC是半径，所以只需证明OC⊥AB即可，设∠BCD为x，则∠COD为2x，通过△OCD内角即可求出∠OCD=90°，即OC⊥AB，所以AB是 ⊙O 的切线。
（2）通过勾股定理定理可以求得AB=5，解直角三角形可知OC=125，先算出直角三角形AOB和扇形OED的面积，阴影部分的面积等于三角形AOB的面积减去扇形OED的面积。
22．【答案】（1）解：设购进每斤A种米线的价格是a元，每斤B种米线的价格是b元，
根据题意得：a+2b=43a+4b=9，
解得：a=1b=1.5．
答：购进每斤A种米线的价格是1元，每斤B种米线的价格是1.5元；
（2）解：∵该店计划在米线节期间每天售出米线共200斤，且每天售出A种米线x斤，
∴每天售出B种米线(200−x)斤．
根据题意得：x≥3(200−x)，
解得：x≥150，
∵米线节期间共计81天的总利润为y元，
∴y=81[(2−1)x+(3.5−1.5)(200−x)]，即y=−81x+32400，
∵−81<0，
∴y随x的增大而减小，
又∵x≥150，
∴当x=150时，y取得最大值，最大值为−81×150+32400=20250．
答：x为150时，总利润y最大，最大总利润为20250元．
【知识点】二元一次方程组的实际应用-销售问题
【解析】【分析】（1）首先设每斤A种米线的价格是a元，每斤B种米线的价格是b元 ，由购进1斤A种米线和2斤B种米线共需花费4元，购进3斤A种米线和4斤B种米线共需花费9元，列出二元一次方程组求解即可。
（2）由每天售出米线共200斤，且每天售出A种米线的数量不少于B种米线的3倍 ，列出不等式，确定A种米线的范围，由A、B两种米线的售价和（1）中求出的进价求出A、B两种米线每斤的利润，由总利润等于每种米线的数量乘以每斤的利润列出关于y与x的函数关系式，由一次函数的增减性以及x的取值范围来确定最大利润。
23．【答案】（1）证明：∵四边形ABCD是矩形，
∴OA=OC=12AC，OB=OD=12BD，AC=BD，
∴OA=OC=OB=OD=12AC=12BD，
∵CE=12AC，
∴CE=OD，
∵CE//BD，即CE//OD，
∴四边形OCED是平行四边形，
又OD=OC，
∴四边形OCED是菱形；
（2）解：ACCF+DG的值不会发生变化，理由：
解：过点D作DH⊥AC于点H，延长GP交AC于点M，
∴∠DHC=90°，
由(1)已证四边形OCED是菱形，
∴DE//OC，
∴∠DHC+∠HDE=180°，
∴∠HDE=90°，
又PG⊥DE，
∴四边形DHMG是矩形，
∴DG=HM，∠HMG=90°，
∴∠PMC=90°，
∵PF⊥CE，
∴∠PFC=90°，
∴∠PMC=∠PFC，
∵四边形OCED是菱形，
∴∠PCM=∠PCF，
在△PMC和△PFC中，
∠PMC=∠PFC∠PCM=∠PCFPC=PC，
∴△PMC≌△PFC(AAS)，
∴CM=CF，
∴CF+DG=CM+HM=CH，
设AB=a，
∵BC=2AB，
∴BC=2a，
∵四边形ABCD是矩形，
∴∠ABC=∠ADC=90°，CD=AB=a，
由勾股定理得AC=AB2+BC2=a2+(2a)2=5a，
∵DH⊥AC，
∴∠DHC=90°，
∴∠ADC=∠DHC，
又∵∠ACD=∠DCH，
∴△ADC∽△DHC，
∴ACCD=CDCH，
∴5aa=aCH，
∴CH=5a5，
∴ACCF+DG=ACCH=5a5a5=5，
即ACCF+DG的值不会发生变化，总等于5．
【知识点】菱形的判定与性质；矩形的判定与性质；四边形-动点问题
【解析】【分析】（1）由CE∥BD，以及CE=12AC，先证明四边形OCED是平行四边形，因为OD=OC即可证明四边形OCED是菱形。
（2） 过点D作DH⊥AC于点H，延长GP交AC于点M，先证明四边DHMG为矩形，在证明△PCM和△PFC全等，可得CM=CF；设AB为a，可得CD=AB=a，由勾股定理可得AC=5a；证明△ADC和△DHC相似，通过线段成比例即可得出结果。
24．【答案】（1）解：将点(0，−12)代入抛物线y=12x2+22x+c，得c=−12．
∴抛物线y=12x2+22x−12．
当12x2+22x−12=0时，解得x=−2±62．
∴r=−2+62，s=−2−62或r=−2−62，s=−2+62．
∴d=|r−s|=6．
综上，c=−12，d=6．
（2）解：M=1或M<1．
证明：．
①当r=−2+62，s=−2−62时：
r2=2−3，r3=36−522，r4=7−43，s2=2+3．
∴M=6(2−3)6(2−3)=1．
②当r=−2−62，s=−2+62时：
r2=2+3，r3=−36+522，r4=7+43，s2=2−3．
∴M=−2(6+3)6(2+3)<0，
∴M<1．
综上，M=1或M<1．
【知识点】二次根式的性质与化简；二次函数的实际应用-几何问题
【解析】【分析】（1）将已知点代入二次函数解析式中即可求得c，将二次函数y=0即可解得与x轴的交点坐标，即可得到r和s的值，由于A、B两点在x轴上，所以AB的距离d就为A、B两点横坐标差的绝对值，从而求出d；
（2）首先将M化简，由于不知A、B两点谁在左边，所以要分两种情况讨论，分别求出r2，r3，r4，s2，然后代入即可确定M和1的大小。种类
售价(单位：元/斤)
A种米线
2
B种米线
3.5