06，山东省枣庄市峄城区2023-2024学年七年级上学期期末数学试题

这是一份06，山东省枣庄市峄城区2023-2024学年七年级上学期期末数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

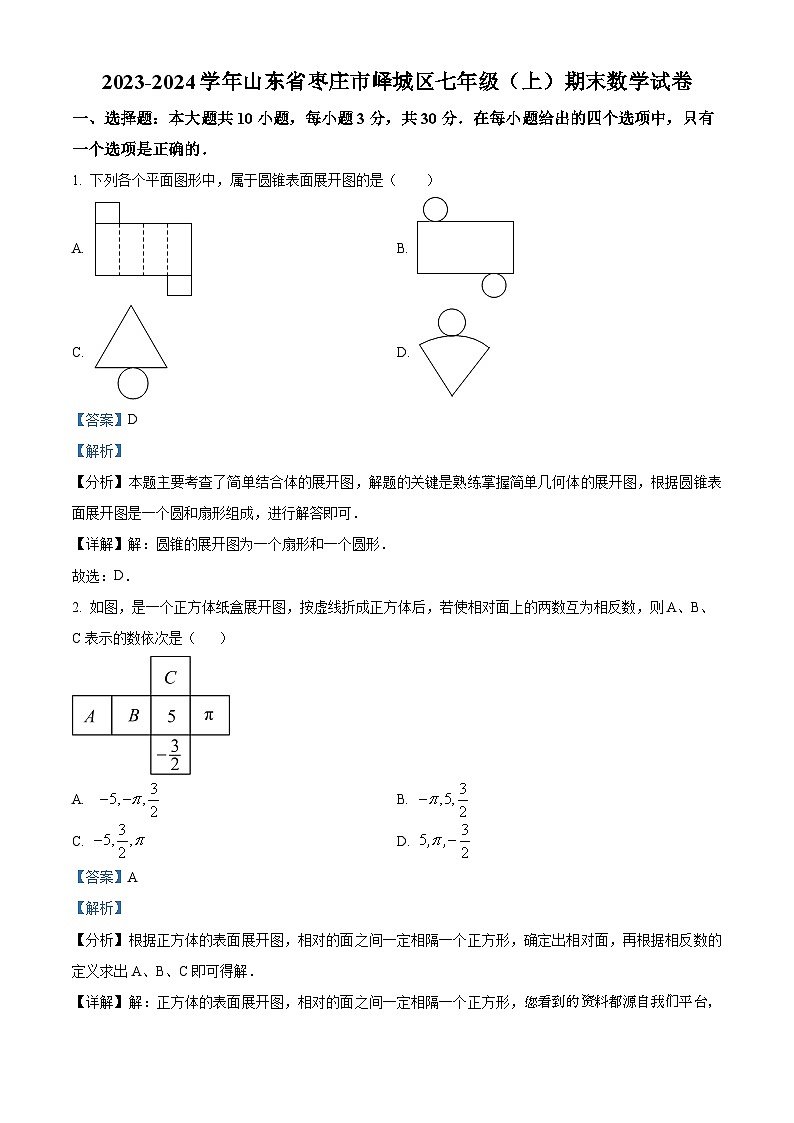
1. 下列各个平面图形中，属于圆锥表面展开图的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题主要考查了简单结合体的展开图，解题的关键是熟练掌握简单几何体的展开图，根据圆锥表面展开图是一个圆和扇形组成，进行解答即可．
【详解】解：圆锥的展开图为一个扇形和一个圆形．
故选：D．
2. 如图，是一个正方体纸盒展开图，按虚线折成正方体后，若使相对面上的两数互为相反数，则A、B、C表示的数依次是（ ）

A. B.
C. D.
【答案】A
【解析】
【分析】根据正方体的表面展开图，相对的面之间一定相隔一个正方形，确定出相对面，再根据相反数的定义求出A、B、C即可得解．
【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，您看到的资料都源自我们平台，家威杏 MXSJ663 免费下载“A”与“5”是相对面，
“B”与“π”是相对面，
“C”与“”是相对面，
∵相对面上的两数互为相反数，
∴A、B、C表示的数依次是-5，-π，．
故选A
【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
3. 在下面的调查中，最适合用全面调查的是（ ）
A. 了解一批节能灯管的使用寿命B. 了解某校803班学生的视力情况
C. 了解某省初中生每周上网时长情况D. 了解京杭大运河中鱼的种类
【答案】B
【解析】
【分析】根据全面调查与抽样调查的特点对四个选项进行判断．
【详解】A、了解一批节能灯管的使用寿命，具有破坏性，适合采用抽样调查，不符合题意；
B、了解某校803班学生的视力情况，适合采用普查，符合题意；
C、了解某省初中生每周上网时长情况，适合采用抽样调查，不合题意；
D、了解京杭大运河中鱼的种类，适合采用抽样调查，不合题意．
故选：B．
【点睛】本题考查了全面调查与抽样调查：如何选择调查方法要根据具体情况而定．一般来讲：通过普查可以直接得到较为全面、可靠的信息，但花费的时间较长，耗费大，且一些调查项目并不适合普查．其二，调查过程带有破坏性．如：调查一批灯泡的使用寿命就只能采取抽样调查，而不能将整批灯泡全部用于实验．其三，有些被调查的对象无法进行普查．
4. 为了加快构建清洁低碳、安全高效的能源体系，国家发布《关于促进新时代新能源高质量发展的实施方案》，旨在锚定到2030年我国风电、太阳能发电总装机容量达到1200000000千瓦以上的目标．数据1200000000用科学记数法表示为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【详解】解：1200000000=1.2×109．
故选：B．
【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
5. 下列计算正确的是( )
A. 4a+2a＝6a2B. 7ab﹣6ba＝abC. 4a+2b＝6abD. 5a﹣2a＝3
【答案】B
【解析】
【分析】直接利用合并同类项法则化简得出答案．
【详解】解：A、4a+2a＝6a，故此选项错误；
B、7ab﹣6ba＝ab，正确；
C、4a+2b无法计算，故此选项错误；
D、5a﹣2a＝3a，故此选项错误；
故选B．
【点睛】此题主要考查了合并同类项法则，正确掌握运算法则是解题关键．
6. 下列画图的语句中，正确的为（ ）
A 画直线AB=10cmB. 画射线OB=10cm
C. 延长射线BA到C，使BA=BCD. 过直线AB外一点画一条直线和直线AB相交
【答案】D
【解析】
【详解】试题解析：A.直线没有长度，错误；
B.射线没有长度，错误；
C.射线没有长度，错误；
D.正确．
故选D
7. 钟表10点30分时，时针与分针所成的角是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据时针与分针相距份数乘以每份的度数，可得答案．
【详解】解：10点30分时的时针和分针相距的份数是4.5，
10点30分时的时针和分针所成的角的度数为30°×4.5=135°，
故选：B.
【点睛】本题考查的知识点是钟面角，解题关键是求出时针和分针之间的格子数，再根据每个格子对应的圆心角的度数，列式解答．
8. 要清楚地表明某地每月的降水量变化情况应该选用哪种统计图？（ ）
A. 条形统计图B. 折线统计图
C. 扇形统计图D. 以上都不对
【答案】B
【解析】
【分析】本题主要考查了统计图的选择，1.条形统计图：用条形统计图可以清楚地表示各种情况下每个项目的具体数目，它的适用范围要广一些；2.折线统计图：折线统计图用于表示同一对象的发展变化情况，用它表示的数据常是在不同的时间或地点从同一个对象身上收集到的；3.扇形统计图：用扇形统计图可以很容易地表示出一个对象在总体中所占的百分比，因此如果需要了解这一方面的信息可选择扇形统计图；解题的关键是熟练掌握三种统计图的特点，根据统计图的特点进行判断即可．
【详解】解：要清楚地表明某地每月的降水量变化情况应该选用折线统计图．
故选：B．
9. 若x＝2是方程4x+2m﹣14＝0的解，则m的值为（ ）
A. 10B. 4C. ﹣3D. 3
【答案】D
【解析】
【分析】把x=2代入已知方程得到m的新方程，通过解新方程求得m的值．
【详解】解：把x=2代入4x+2m-14=0，得
4×2+2m-14=0，
解得m=3．
故选：D．
【点睛】本题考查了一元一次方程的解的定义．方程的解就是能够使方程左右两边相等的未知数的值．
10. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一，书中记载一道问题：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天可以追上慢马？若设快马x天可以追上慢马，则下列方程正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】设快马x天可以追上慢马，根据路程=速度×时间，即可得出关于x的一元一次方程，此题得解．
【详解】解：设快马x天可以追上慢马，
依题意，得： 240x-150x=150×12．
故选：D．
【点睛】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．
二、填空题：本题共6小题，每小题填对得3分，共18分.只要求在答题纸上填写最后结果.
11. 若，则___．
【答案】1
【解析】
【分析】根据绝对值和偶次方的非负数的性质列方程求出a、b的值，然后代入计算即可得解．
【详解】解：，
，
解得，
．
故答案为：1．
【点睛】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0是解题关键．
12. 单项式的系数是_________，次数为___________．
【答案】 ①. ②. 3次
【解析】
【分析】单项式的次数是所含所有字母指数的和，系数就是前面的数字，由此即可求解．
【详解】单项式的系数是，
次数为所含字母指数的和，故次数是3.
故答案为，3.
13. 如图，C，D，E是线段AB上的三个点，下面关于线段CE的表示：
①CE=CD+DE； ②CE=BC﹣EB；
③CE=CD+BD﹣AC； ④CE=AE+BC﹣AB．
其中正确的是_____（填序号）．
【答案】①②④
【解析】
【详解】解：①CE=CD+DE正确．
②，正确．
③，错误．
④，正确．
①②④正确．
故答案为：①②④
14. 如图，把一张长方形的纸按图那样折叠后，、两点落在、若得，则的度数为_______．

【答案】
【解析】
【分析】根据折叠的性质可得，再根据，可得出的度数．
【详解】解：根据折叠的性质得：，
∵，
∴，
∴．
故答案为：．
【点睛】本题考查了折叠的性质，邻补角，解答的关键是结合图形分析清楚角与角之间的关系．
15. 某书店把一本新书按标价的八折出售，仍获利30%，若该书的进价为40元，则标价为_____元．
【答案】65
【解析】
【分析】根据题意，实际售价=进价+利润，八折即标价的80%；可得一元一次的等量关系式，求解可得答案．
【详解】设标价是x元，根据题意有：
0.8x=40(1+30%)，
解得：x=65.
故标价为65元.
故答案为65.
【点睛】考查一元一次方程的应用，掌握利润=售价-进价是解题的关键.
16. 当今大数据时代，“二维码”具有存储量大．保密性强、追踪性高等特点，它已被广泛应用于我们的日常生活中，尤其在全球“新冠”疫情防控期间，区区“二维码”已经展现出无穷威力．看似“码码相同”，实则“码码不同”．通常，一个“二维码”由1000个大大小小的黑白小方格组成，其中小方格专门用做纠错码和其他用途的编码，这相当于1000个方格只有200个方格作为数据码．根据相关数学知识，这200个方格可以生成个不同的数据二维码，现有四名网友对的理解如下：
YYDS（永远的神）：就是200个2相乘，它是一个非常非常大的数；
DDDD（懂的都懂）：等于；
JXND（觉醒年代）：个位数字是6；
QGYW（强国有我）：我知道，所以我估计比大．
其中对的理解错误的网友是___________（填写网名字母代号）．
【答案】DDDD
【解析】
【分析】根据乘方的含义即可判断YYDS（永远的神）的理解是正确的；根据积的乘方的逆用，将化为，再与比较，即可判断DDDD（懂的都懂）的理解是错误的；根据2的乘方的个位数字的规律即可判断JXND（觉醒年代）的理解是正确的；根据积的乘方的逆用可得，即可判断QGYW（强国有我）的理解是正确的．
【详解】是200个2相乘，YYDS（永远的神）的理解是正确的；
，DDDD（懂的都懂）的理解是错误的；
，
2的乘方的个位数字4个一循环，
，
的个位数字是6，JXND（觉醒年代）的理解是正确的；
，，且
，故QGYW（强国有我）的理解是正确的；
故答案为：DDDD．
【点睛】本题考查了乘方含义，幂的乘方的逆用等，熟练掌握乘方的含义以及乘方的运算法则是解题的关键．
三、解答题：本题共8小题，满分72分.解答应写出必要的文字说明或演算步骤.
17. 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
（1）先计算乘法，再算加减，即可解答；
（2）先把有理数的除法转化为乘法，然后再利用乘法分配律进行计算，即可解答．
【小问1详解】
解：
；
【小问2详解】
解：
．
18. 先化简，再求值：
(4x2-4y2)-3(x2y2+x2)+3(x2y2+y2)，其中x=-1，y=2．
【答案】-3
【解析】
【分析】先根据去括号法则去括号，再合并同类项，完成化简，最后代入求值即可．
【详解】解：(4x2-4y2)-3(x2y2+x2)+3(x2y2+y2)
=4x2-4y2-3x2y2-3x2+3x2y2+3y2
=x2-y2
当 x=-1，y=2时，原式=（-1）2-22=-3
19. 解下列方程：
（1）；
（2）.
【答案】19.
20.
【解析】
【分析】本题考查了解一元一次方程：
（1）去括号，再移项合并同类项，系数化1，即可作答．
（2）先去分母，再移项合并同类项，系数化1，即可作答．
【小问1详解】
解：去括号得：，
移项合并得：，
解得：；
【小问2详解】
解：去分母得：，
去括号，得
移项合并得：，
解得： ．
20. 作图：
如图①是一些小正方体所搭立体图形从上面看得到的图形，方格中的数字表示该位置的小正方体的个数．请在如图②所示的方格纸中分别画出这个立体图形从正面看和从左面看得到的图形．
【答案】见解析
【解析】
【分析】本题是考查作图简单图形的三视图，解题的关键是能正确辨认从正面、上面、左面观察到的简单几何体的平面图形．根据图中所示各位置小正方体的个数，从正面能看到6个正方形，分三列，各列从左到右分别是3个、1个、2个；从左面能看到6个正方形，分三列，各列从左到右分别是3个、2个、1个．
【详解】解：如图：
21. 某校计划组织学生外出开展研学活动，在选择研学活动地点时，随机抽取了部分学生进行调查，要求被调查的学生从A、B、C、D、E五个研学活动地点中选择自己最喜欢的一个．根据调查结果，编制了如下两幅不完整的统计图．

（1）请把图1中缺失的数据，图形补充完整；
（2）请计算图2中研学活动地点C所在扇形的圆心角的度数；
（3）若该校共有1200名学生，请估计最喜欢去D地研学的学生人数．
【答案】（1）见解析；
（2）；
（3）300．
【解析】
【分析】（1）根据选择的人数是人，所占的比例是，据此即可求得本次参加抽样调查的学生人数，进而求得选择的人数，即可补全统计图；
（2）利用乘以选择的人数所占总人数的比即可得解；
（3）利用总人数乘以对应的百分比即可求得．
【小问1详解】
解：（人）
选择的人数：（人）
补全图形如下：
【小问2详解】
解：，
∴研学活动地点所在扇形的圆心角的度数；
【小问3详解】
（人）
答：最喜欢去地研学的学生人数共有人．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
22. 如图，OM是∠AOC的平分线，ON是∠BOC的平分线．
（1）如图1，当∠AOB＝90°，∠BOC＝60°时，∠MON的度数是多少？为什么？
（2）如图2，当∠AOB＝70°，∠BOC＝60°时，∠MON＝_______（直接写出结果）．
（3）如图3，当∠AOB＝α，∠BOC＝β时，猜想：∠MON＝_______（直接写出结果）．
【答案】（1）∠MON＝45°，原因见解析；（2）35°；（3）
【解析】
【分析】(1)求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC-∠NOC求出即可；
(2)求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC-∠NOC求出即可；
(3)求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC-∠NOC求出即可．
【详解】解：（1）如图1，∵∠AOB＝90°，∠BOC＝60°，
∴∠AOC＝90°+60°＝150°，
∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC＝∠AOC＝75°，∠NOC＝∠BOC＝30°
∴∠MON＝∠MOC﹣∠NOC＝45°．
（2）如图2，
∵∠AOB＝70°，∠BOC＝60°，
∴∠AOC＝70°+60°＝130°，
∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC＝∠AOC＝65°，∠NOC＝∠BOC＝30°
∴∠MON＝∠MOC﹣∠NOC＝65°﹣30°＝35°．
故答案为：35°．
（3）如图3，∠MON＝α，与β的大小无关．
理由：∵∠AOB＝α，∠BOC＝β，
∴∠AOC＝α+β．
∵OM是∠AOC的平分线，ON是∠BOC的平分线，
∴∠MOC＝∠AOC＝（α+β），
∠NOC＝∠BOC＝β，
∴∠MON＝∠MOC﹣∠NOC
＝（α+β）﹣β＝α
即∠MON＝α．
故答案为：α．
【点睛】本题考查了角平分线定义和角的有关计算，求出∠AOC、∠MOC、∠NOC的度数，并且得到∠MON=∠MOC-∠NOC这个关系式是解题的关键．
23. 情境：
请根据图中的信息，解答下列问题：
（1）购买6根跳绳需______元，购买12根跳绳需______元；
（2）小红比小明多买2根，付款时小红反而比小明少5元．你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由．
【答案】（1）150，240
（2）有这种可能，小红购买跳绳11根，理由见解析
【解析】
【分析】（1）根据单价×数量=总价,求出6根跳绳需多少元；购买12根跳绳，超过10根，打八折是指现价是原价的80%，用单价×数量×0.8即可求出购买12根跳绳需多少元；
（2）有这种可能，可以设小红购买x根跳绳，那么小明购买x-2根跳绳，列出方程25x×0.8=25（x-2）-5，解答即可．
【小问1详解】
6×25＝150（元），12×25×0.8＝240（元）
【小问2详解】
有这种可能
设小红购买跳绳x根，
根据题意得25×80%x＝25（x－2）－5，
解得x＝11.
因此小红购买跳绳11根．
【点睛】解答的关键是读懂题意，根据题目给出的条件，找出合适的等量关系，列出方程进行解答即可．
24. 如图，P是线段AB上一点，AB=12cm，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上），运动的时间为t.
（1）当t=1时，PD=2AC，请求出AP的长；
（2）当t=2时，PD=2AC，请求出AP的长；
（3）若C、D运动到任一时刻时，总有PD=2AC，请求出AP的长；
（4）在（3）的条件下，Q是直线AB上一点，且AQ﹣BQ=PQ，求PQ的长.
【答案】（1）4cm；（2）4cm；（3）4cm；（4）4cm或12cm
【解析】
【分析】(1) 观察图形可以看出，图中的线段PC和线段BD的长分别代表动点C和D的运动路程. 利用“路程等于速度与时间之积”的关系可以得到线段PC和线段BD的长，进而发现BD=2PC. 结合条件PD=2AC，可以得到PB=2AP. 根据上述关系以及线段AB的长，可以求得线段AP的长.
(2) 利用“路程等于速度与时间之积”的关系结合题目中给出的运动时间，可以求得线段PC和线段BD的长，进而发现BD=2PC. 根据BD=2PC和PD=2AC的关系，依照第(1)小题的思路，可以求得线段AP的长.
(3) 利用“路程等于速度与时间之积”的关系可知，只要运动时间一致，点C与点D运动路程的关系与它们运动速度的关系一致. 根据题目中给出的运动速度的关系，可以得到BD=2PC. 这样，本小题的思路就与前两个小题的思路一致了. 于是，依照第(1)小题的思路，可以求得线段AP的长.
(4) 由于题目中没有指明点Q与线段AB的位置关系，所以应该按照点Q在线段AB上以及点Q在线段AB的延长线上两种情况分别进行求解. 首先，根据题意和相关的条件画出相应的示意图. 根据图中各线段之间的关系并结合条件AQ-BQ=PQ，得到AP和BQ之间的关系，借助前面几个小题的结论，即可求得线段PQ的长.
【详解】(1) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t=1(s)，所以(cm).
因为点D从B出发以2(cm/s)的速度运动，运动的时间为t=1(s)，所以(cm).
故BD=2PC.
因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm，所以(cm).
(2) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t=2(s)，所以(cm).
因为点D从B出发以2(cm/s)的速度运动，运动的时间为t=2(s)，所以(cm).
故BD=2PC.
因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm，所以(cm).
(3) 因为点C从P出发以1(cm/s)的速度运动，运动的时间为t(s)，所以(cm).
因为点D从B出发以2(cm/s)的速度运动，运动的时间为t(s)，所以(cm).
故BD=2PC.
因为PD=2AC，BD=2PC，所以BD+PD=2(PC+AC)，即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm，所以(cm).
(4) 本题需要对以下两种情况分别进行讨论.
(i) 点Q在线段AB上(如图①).
因为AQ-BQ=PQ，所以AQ=PQ+BQ.
因为AQ=AP+PQ，所以AP=BQ.
因为，所以.
故.
因为AB=12cm，所以(cm).
(ii) 点Q不在线段AB上，则点Q在线段AB的延长线上(如图②).
因为AQ-BQ=PQ，所以AQ=PQ+BQ.
因为AQ=AP+PQ，所以AP=BQ.
因为，所以.
故.
因为AB=12cm，所以(cm).
综上所述，PQ长为4cm或12cm.
【点睛】本题是一道几何动点问题. 分析图形和题意，找到代表动点运动路程的线段是解决动点问题的重要环节. 利用速度、时间和路程的关系，常常可以将几何问题与代数运算结合起来，通过运算获得更多的线段之间的关系，从而为解决问题提供有利条件. 另外，分情况讨论的思想也是非常重要的，在思考问题时要注意体会和运用.