

所属成套资源:2024年中考数学专题训练【专题训练+能力提升】(原卷版+解析)
2024年中考数学专题训练 专题12 两之间线段最短求最值(四大类型含将军饮马)(能力提升)(原卷版+解析)
展开
这是一份2024年中考数学专题训练 专题12 两之间线段最短求最值(四大类型含将军饮马)(能力提升)(原卷版+解析),共23页。试卷主要包含了【问题提出】等内容,欢迎下载使用。
(能力提升)
1.【问题提出】
(1)如图①,某牧马人要从A地前往B地,途中要到旁边一条笔直的河边l喂马喝一次水,经测量A点到河边的距离AC为300米,B点到河边的距离BD为900米,且点C、D间距离为900米,请计算该牧马人的最短路径长;
【问题探究】
(2)如图②,在△ABC中,AB=AC,BC=6,AC的中垂线分别交AB,AC的边于E,F,△ABC的面积为24,若点D是BC边的中点,点M是线段EF上的一动点,请求出△CDM周长的最小值;
【问题解决】
(3)如图③所示,某工厂生产车间的平面示意图为四边形ABCD,∠C=∠D=90°,AD=70m,CD=60m,BC=110m,在AB的中点处有一个出货口M,在BC上有一个质检口N,点D为货物包装口.为了使得该生产车间出货——质检——包装过程达到最高效率,现要求从出货口M到质检口N的距离MN与质检口到包装口D的距离ND之和最短(即MN+ND最短).请根据要求计算出MN+ND的最小值为多少?
2.如图①,在菱形ABCD中,BD为对角线,过点A作AE⊥BC于点E,交BD于点F,其中2BE=BC,DF=.
(1)求EF的长;
(2)如图②,点G为CD上一点,过点G作GH⊥AD于点H,交BD于点M,在AE上取点N,使AN=2HM,连接BN,CM,求证:BN=CM;
(3)如图③,将△ABD沿射线BD的方向平移得到△A'B'D',连接A'C,A'D,B'C,求A'C+A'D的最小值.
3.(1)如图①,在等边△ABC中,BC=4,点P是BC上一动点,点P关于直线AB,AC的对称点分别为点M,N,连接MN.
①当点P与点B重合时,线段MN的长是 ,
当AP的长最小时,线段MN的长是 ;
②如图②,PM,PN分别交AB,AC于点D,E.当PB=1时,求线段MN的长;
(2)如图③,在等腰△ABC中,∠BAC=30°,AB=AC,点P,Q,R分别为边BC,AB,AC上(均不与端点重合)的动点,当△PQR的周长最小时,求∠PQR+∠PRQ的度数.
4.如图①,在正方形ABCD中,点E为AB上的一个点,作射线DE交CB的延长线于点F,过点C作CM⊥DE交AD于点M,交DE于点N,连接AF.
(1)当点E为AB的中点时.
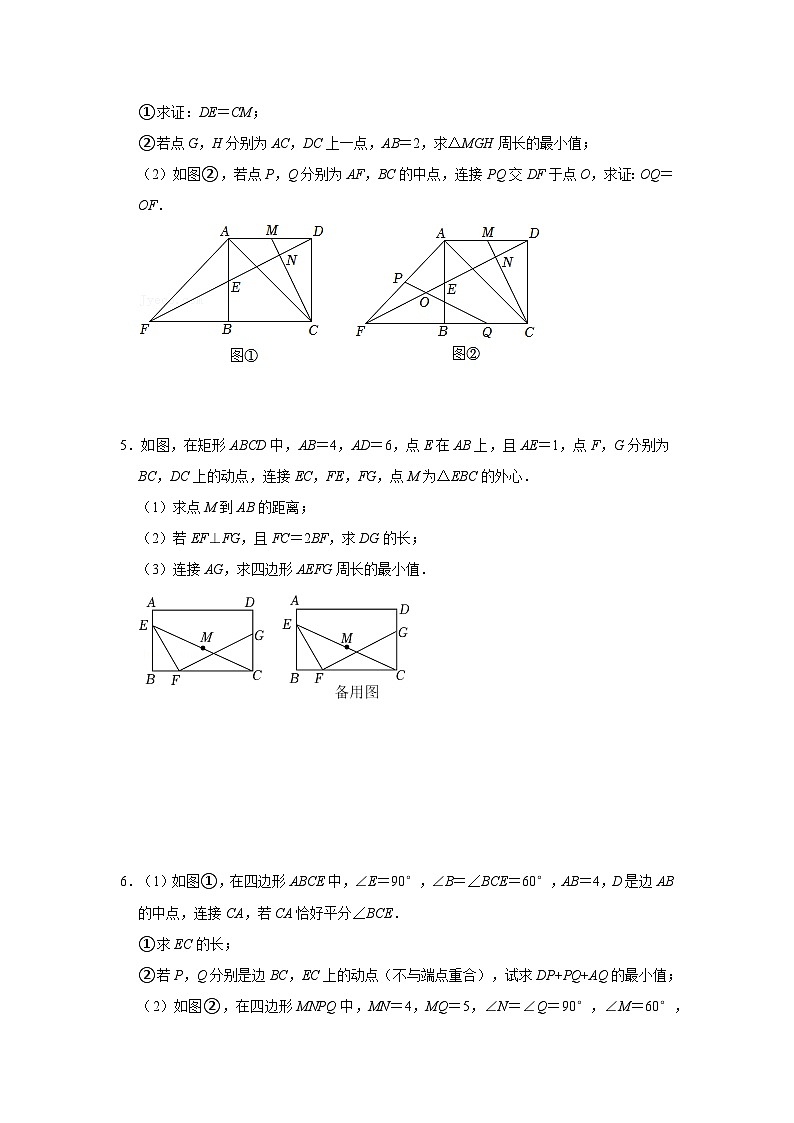
①求证:DE=CM;
②若点G,H分别为AC,DC上一点,AB=2,求△MGH周长的最小值;
(2)如图②,若点P,Q分别为AF,BC的中点,连接PQ交DF于点O,求证:OQ=OF.
5.如图,在矩形ABCD中,AB=4,AD=6,点E在AB上,且AE=1,点F,G分别为BC,DC上的动点,连接EC,FE,FG,点M为△EBC的外心.
(1)求点M到AB的距离;
(2)若EF⊥FG,且FC=2BF,求DG的长;
(3)连接AG,求四边形AEFG周长的最小值.
6.(1)如图①,在四边形ABCE中,∠E=90°,∠B=∠BCE=60°,AB=4,D是边AB的中点,连接CA,若CA恰好平分∠BCE.
①求EC的长;
②若P,Q分别是边BC,EC上的动点(不与端点重合),试求DP+PQ+AQ的最小值;
(2)如图②,在四边形MNPQ中,MN=4,MQ=5,∠N=∠Q=90°,∠M=60°,点A,B,C,D分别在边MQ,MN,NP,QP上,若AQ=1,求四边形ABCD周长的最小值.
7.如图,在矩形ABCD中,AB=4,BC=2,点E,F分别是AB,CD边上的点(不与点B,D重合),且EF⊥AC,EF与AC交于点O.
(1)请在①OA=OC;②∠EFC=∠ECF;③AF∥CE;④AF=AE中选择一个条
件 (填序号),使得四边形AECF为菱形,并加以证明(选择一个即可);
(2)求EF的值;
(3)求AF+EF+CE的最小值.
8.如图①,在正方形ABCD中,点E,F分别是BC,CD边上的动点(均不与正方形的顶点重合),且∠EAF=45°,连接EF.
(1)求证.EF=BE+DF;
(2)如图②,点P是EF的中点,连接AP,作点E关于直线AB的对称点E',作点F关于直线AD的对称点F',连接E'F',求证:E'F'=2AP;
(3)如图③,正方形ABCD是李叔叔家菜地示意图,其中AB=800米,李叔叔计划在菜地中开拓一条小路EM﹣MN﹣NF,其中点E为AB的中点,点F为CD边上一点,且CF=300米,点M,N在线段BC上(点M在点N的左侧),且MN=100米.为了尽可能少的破坏植物,需要以最小长度来修建,请你帮李叔叔计算这条小路长度的最小值.(结果保留整数,参考数据:≈1.41,≈1.73)
专题12 两之间线段最短求最值(四大类型含将军饮马)
(能力提升)
1.【问题提出】
(1)如图①,某牧马人要从A地前往B地,途中要到旁边一条笔直的河边l喂马喝一次水,经测量A点到河边的距离AC为300米,B点到河边的距离BD为900米,且点C、D间距离为900米,请计算该牧马人的最短路径长;
【问题探究】
(2)如图②,在△ABC中,AB=AC,BC=6,AC的中垂线分别交AB,AC的边于E,F,△ABC的面积为24,若点D是BC边的中点,点M是线段EF上的一动点,请求出△CDM周长的最小值;
【问题解决】
(3)如图③所示,某工厂生产车间的平面示意图为四边形ABCD,∠C=∠D=90°,AD=70m,CD=60m,BC=110m,在AB的中点处有一个出货口M,在BC上有一个质检口N,点D为货物包装口.为了使得该生产车间出货——质检——包装过程达到最高效率,现要求从出货口M到质检口N的距离MN与质检口到包装口D的距离ND之和最短(即MN+ND最短).请根据要求计算出MN+ND的最小值为多少?
【解答】解:(1)如图①中,作点A关于直线l的对称点A′,连接BA′交直线l于点P,连接PA,此时PA+PB的值最小,最小值为线段BA′的长.
过点B作BT⊥AA′交A′A的延长线于点T.
在Rt△A′BT中,BT=CD=900米.AT=1200米,
∴BA′===1500(米),
∴该牧马人的最短路径长为1500米;
(2)如图②中,连接AD,AM.
∵AB=AC,AD是中线,
∴AD⊥BC,BD=CD=3,
∵S△ABC=×BC×AD=24,BC=6,
∴AD=8,
∵EF垂直平分线段AC,
∴MA=MC,
∴MD+MC=AM+MD≥AD=8,
∴MD+MC的最小值为8,
∴△CDM的周长的最小值为11;
(3)如图③中,延长DC到R,使得CR=DC,连接MR,过点M作MQ⊥CD于点Q.
∵BC⊥DR,CD=CR,
∴ND=NR,
∴MN+ND=MN+NR≥MR,
∵AM=BM,AD∥MQ∥BC,
∴DQ=CQ=30m,
∴MQ=(AD+BC)=90(m),
∴MR===90(m),
∴MN+DN≥90,
∴MN+ND的最小值为90m.
2.如图①,在菱形ABCD中,BD为对角线,过点A作AE⊥BC于点E,交BD于点F,其中2BE=BC,DF=.
(1)求EF的长;
(2)如图②,点G为CD上一点,过点G作GH⊥AD于点H,交BD于点M,在AE上取点N,使AN=2HM,连接BN,CM,求证:BN=CM;
(3)如图③,将△ABD沿射线BD的方向平移得到△A'B'D',连接A'C,A'D,B'C,求A'C+A'D的最小值.
【解答】(1)解:如图①,连接AC,
∵四边形ABCD是菱形,
∴AB=CB=AD=CD,AC⊥BD,AD∥BC,
∴∠DAF=∠BEF=90°,
∵AE⊥BC,2BE=BC,DF=,
∴BE=CE=BC,
∴AB=AC=CB=AD=CD,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠ADC=∠BAC=60°,
∴∠EBF=∠ABC=30°,∠ADF=∠ADC=30°,
∴BC=AD=DF•cs30°=×=1,
∴BE=×1=,
∴EF=BE•tan30°=×=,
∴EF的长是.
(2)证明:如图②,∵GH⊥AD,∠HDM=30°,
∴∠DHM=90°,
∴DM=2HM,
∵AN=2HM,
∴AN=DM,
∵∠BAN=∠BAC=30°,∠CDM=∠ADC=30°,
∴∠BAN=∠CDM,
∴△ABN≌△DCM(SAS),
∴BN=CM.
(3)如图③,连接AC交BD于点O,作直线AA′,由平移得AA′∥BD;
作点D关于AA′的对称点G,连接CG交AA′于点H、交AD于点L,连接DG交AA′于点R,连接DH,
∵AA′垂直平分DG,
∴∠ARD=90°,
∴∠OAR=∠AOB=∠AOD=90°,
∴四边形AODR是矩形,
∴DR=OA,
∵DG=2DR,DC=AC=2OA,
∴DG=DC=1,
∵∠LDG=∠LDC=∠DAC=60°,
∴DL⊥CG,
∴CL=GL,∠DLC=90°,
∴CL=CD•sin60°=1×=,
∴CG=2CL=2×=,
∵A′G=A′D,
∴A′C+A′D=A′C+A′G,
∵A′C+A′G≥CG,
∴当点A′与点H重合时,A′C+A′G=CG=,此时A′C+A′G的值最小,
∴A′C+A′D的最小值为.
3.(1)如图①,在等边△ABC中,BC=4,点P是BC上一动点,点P关于直线AB,AC的对称点分别为点M,N,连接MN.
①当点P与点B重合时,线段MN的长是 ,
当AP的长最小时,线段MN的长是 ;
②如图②,PM,PN分别交AB,AC于点D,E.当PB=1时,求线段MN的长;
(2)如图③,在等腰△ABC中,∠BAC=30°,AB=AC,点P,Q,R分别为边BC,AB,AC上(均不与端点重合)的动点,当△PQR的周长最小时,求∠PQR+∠PRQ的度数.
【解答】解:(1)如图①﹣1中,当点P与B重合时,设PN交AC于点T.
∵P,N关于AC对称,
∴PN⊥AC,
∵△ABC是等边三角形,
∴AB=BC=AC=4,
∴AT=CT=2,
∵BT=TN==2,
∴MN=4,
如图①﹣2中,连接AM,AN.
当AP⊥BC时,AP=2,
∵P,M关于AB对称,P,N关于AC对称,
∴AM=AP=AN,∠BAP=∠BAM,∠PAC=∠NAC,
∴∠MAN=2∠BAC=120°,
∴MN=AM=AP=6,
故答案为:4,6;
②如图②中,连接AM,AN.作AH⊥BC于点H.
∵AB=AC=BC=4,AH⊥CB,
∴BH=CH=2,
∵PB=1,
∴PH=1,
∴AP===.
∵P,M关于AB对称,P,N关于AC对称,
∴PM=PM=PA=,
∵∠MAN=120°,
∴MN=AM=;
(2)作点P关于AB的对称点P',作P关于AC的对称点P'',连接P'P'',分别交AB、AC于点Q、R,连接AP'、AP''.
则P'Q=PQ,P''R=PR,AP=AP'=AP'',∠P'AQ=∠PAQ,∠P''AR=∠PAR,
∴△PQR周长=PQ+QR+PR=P'Q+QR+P''R=P'P'',
∠P'AP''=∠P'AQ+∠PAQ+∠P''AR+∠PAR=2∠BAC=2×30°=60°,
∴△AP'P''为等边三角形,
∴P'P''=AP=AP'=AP'',
当AP⊥BC时,AP最短,即为△PQR周长的最小值,
此时∠P′=∠APQ=60°,∠P″=∠APR=60°,
∴∠QPR=120°,
∴∠PQR+∠PRQ=60°.
4.如图①,在正方形ABCD中,点E为AB上的一个点,作射线DE交CB的延长线于点F,过点C作CM⊥DE交AD于点M,交DE于点N,连接AF.
(1)当点E为AB的中点时.
①求证:DE=CM;
②若点G,H分别为AC,DC上一点,AB=2,求△MGH周长的最小值;
(2)如图②,若点P,Q分别为AF,BC的中点,连接PQ交DF于点O,求证:OQ=OF.
【解答】(1)①证明:∵CM⊥DE,
∴∠CND=90°,
∴∠NCD+∠NDC=90°,
∵四边形ABCD为正方形,
∴∠BAD=∠ADC=90°,AD=DC,
∴∠ADE+∠NDC=90°,
∴∠ADE=∠DCM,
∴△ADE≌△DCM(ASA),
∴DE=CM;
②解:由(1)①得,△ADE≌△DCM,
∴DM=AE.
∵点E为AB的中点,
∴DM=AE=1/2AB,即点M为AD的中点,
∴点M与点E关于AC对称,
如图,作点M关于DC的对称点M′,连接EM′交AC于点G,交DC于点H,连接MG,MH.
∵△MGN的周长=MG+MH+GH=EG+HM′+GH≥EM′,当且仅当E,G,H,M′四点共线时取等号,
∴△MGH周长的最小值为EM′的长.
∵AB=2,
∴DM′=DM=AE=1,
∴AM′=3,
∴EM′==,
∴△MGH周长的最小值为;
(2)证明:如图,过点P作PT∥AD交DF于点T,连接PB,TQ,
∵点P为AF的中点,
∴PT=AD.
∵AD=BC,AD∥BC,点Q为BC的中点,
∴PT∥BQ,PT=BC=BQ,
∴四边形PTQB为平行四边形,
∴TQ∥PB,TQ=PB.
在Rt△ABF中,
∵点P为AF的中点,
∴PB=AF=PF,
∴TQ=PF,∠PFB=∠PBF=∠TQF.
在△PFQ和△TQF中,
,
∴△PFQ≌△TQF(SAS),
∴∠PQF=∠TFQ,
∴OQ=OF.
5.如图,在矩形ABCD中,AB=4,AD=6,点E在AB上,且AE=1,点F,G分别为BC,DC上的动点,连接EC,FE,FG,点M为△EBC的外心.
(1)求点M到AB的距离;
(2)若EF⊥FG,且FC=2BF,求DG的长;
(3)连接AG,求四边形AEFG周长的最小值.
【解答】解:(1)这MN⊥AB于N,
∵点M为△EBC的外心,
∴EM=MC,
∵MN∥BC,
∴EN=BN,
∴MN=BC=3;
(2)∵EF⊥FG,
∴∠GFC+∠EFB=∠BEF+∠EFB=90°,
∴∠GFC=∠BEF,
∵∠EBF=∠FCG,
∴△EBF∽△FCG,
∴BF:CG=EB:FC,
∴2:CG=3:4,
∴CG=;
(3)作A关于DC的对称点Q,连接CQ,
作E关于BC的对称点P,连接PF,连接PQ,
当点P,F,G,Q共线时,四边形AEFG的周长最小,
∵PQ2=PA2+QA2,
∴PQ2=72+122,
∴PQ=,
∴四边形AEFG的周长最小值为:+1.
6.(1)如图①,在四边形ABCE中,∠E=90°,∠B=∠BCE=60°,AB=4,D是边AB的中点,连接CA,若CA恰好平分∠BCE.
①求EC的长;
②若P,Q分别是边BC,EC上的动点(不与端点重合),试求DP+PQ+AQ的最小值;
(2)如图②,在四边形MNPQ中,MN=4,MQ=5,∠N=∠Q=90°,∠M=60°,点A,B,C,D分别在边MQ,MN,NP,QP上,若AQ=1,求四边形ABCD周长的最小值.
【解答】解:(1)①如图①中,∵AC平分∠BCE,
∴∠ACB=∠ACE=∠BCE=30°,
∵∠B=60°,
∴∠BAC=90°,
∴AC=AB=4,
∵∠E=90°,
∴EC=AC•cs30°=4×=6;
②如图①中,作点D关于BC的对称点D′,作点A关于EC的对称点A′,连接A′D′交BC于点P,交EC于点Q,连接DP,AQ,此时DP+PQ+AQ的值最小,最小值为A′D′的长,
连接A′C,过点D′作D′T⊥A′C于点T.设DD′交BC于点J.
∴A,A′关于EC的长,
∴∠ECA′=∠ECA=30°,
∵∠BCE=60°,
∴∠A′CB=∠BCT=90°,
∵∠T=∠D′JC=90°,
∴四边形CJD′T是矩形,
∵BD=AD=2,∠DJB=90°,∠B=60°,
∴BJ=1,DJ=JD′=,
∵BC=2AB=8,
∴CJ=TD′=7,
∵CA′=AC=4,CT=JD′=,
∴A′T=5,
∴A′D′===2,
∴DP+PQ+AQ的最小值为2;
(3)如图②中,作点A关于PQ的对称点E,点A关于MN的对称点F,点B关于PN的对称点G,点F关于PN的对称点H,连接BF,CG,DE,GH,EH,过点E作ET⊥FH于T交MN于K,设AF交MN于J.
由对称性可知,DA=DE,CB=CG,AB=BF,BF=GH,
∴AD+CD+CB+AB=DE+CD+CB+BF=ED+CD+CG+GH≥EH,
在Rt△AMJ中,∠AJM=90°,AM=MQ﹣AQ=5﹣1=4,∠M=60°,
∴MJ=AM•cs60°=2,AJ=JF=KT=2,
∴JN=MN﹣MJ=4﹣2=2,
∴FH=2JN=4,
在Rt△EMK中,EK=EM•sin60°=3,BM=EM•cs60°=3,
∴TE=EK+KT=5,JK=FT=MK﹣MJ=1,TH=FH﹣FT=4﹣1=3,
∴EH==2,
∴当E,D,C,G,H共线时,AD+CD+CB+BA的值最小,最小值为2.
7.如图,在矩形ABCD中,AB=4,BC=2,点E,F分别是AB,CD边上的点(不与点B,D重合),且EF⊥AC,EF与AC交于点O.
(1)请在①OA=OC;②∠EFC=∠ECF;③AF∥CE;④AF=AE中选择一个条
件 (填序号),使得四边形AECF为菱形,并加以证明(选择一个即可);
(2)求EF的值;
(3)求AF+EF+CE的最小值.
【解答】解:(1)①③④都满足条件.
当OA=OC时,∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FCO=∠EAO,
在△FCO和△EAO中,
,
∴△FCO≌△EAO(ASA),
∴CF=AE,
∵CF∥AE,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形;
当AF∥EC时,∵CF∥AE,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形;
当AE=AE时,∵AC⊥EF,
∴OF=OE,
同法可证△FCO≌△EAO,
∴CF=AE,
∵CF∥AE,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形;
故答案为:①③④;
(2)如图,过点F作FH⊥AB于点H.
∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,AB=CD=4,AD=BC=2,
∴AC===2,
∵FH⊥AB,AC⊥EF,
∴∠D=∠FHE=∠AOE=∠DAH=90°,
∴四边形ADFH是矩形,
∴FH=AD=2,
∵∠DAC+∠CAB=90°,∠CAB+∠FEH=90°,
∴∠DAC=∠FEH,
∴△CDA∽△FHE,
∴=,
∴=,
∴EF=;
(3)设DF=x.
在Rt△EFH中,EH===1,
∵四边形ADFH是矩形,
∴AH=DF=x,
∴EB=4﹣x﹣1=3﹣x,
∴AF+EC=+,
欲求AE+EC的最小值,相当于在x轴上找一点M(x,0),使得点M到,P(0,2),Q(3,2)的距离和最小,如图1中,
作点P关于x轴的对称点P′,连接QP′交x轴于点M,连接PM,此时PM+MQ的值最小,最小值=QP′的长,
∵P′(0,﹣2),Q(3,2),
∴QP′==5,
∴AF+EC的最小值为5,
∴AF+EF+CE的最小值为5+.
8.如图①,在正方形ABCD中,点E,F分别是BC,CD边上的动点(均不与正方形的顶点重合),且∠EAF=45°,连接EF.
(1)求证.EF=BE+DF;
(2)如图②,点P是EF的中点,连接AP,作点E关于直线AB的对称点E',作点F关于直线AD的对称点F',连接E'F',求证:E'F'=2AP;
(3)如图③,正方形ABCD是李叔叔家菜地示意图,其中AB=800米,李叔叔计划在菜地中开拓一条小路EM﹣MN﹣NF,其中点E为AB的中点,点F为CD边上一点,且CF=300米,点M,N在线段BC上(点M在点N的左侧),且MN=100米.为了尽可能少的破坏植物,需要以最小长度来修建,请你帮李叔叔计算这条小路长度的最小值.(结果保留整数,参考数据:≈1.41,≈1.73)
【解答】(1)证明:如图①中,延长CB至K,使得BK=DF,连接AK,则△ABK≌△ADF,
∴AK=AF,∠BAK=∠DAF,
∴∠EAK=∠EAB+∠BAK=∠EAB+∠DAF=90°﹣∠EAF=45°,
∴∠EAK=∠EAF,
在△EAK和△EAF中,
,
∴△EAK≌△EAF(SAS),
∴EF=EK=BK+BE=DF+BE;
(2)证明:如图②中,延长AP至T,使得PT=AP,连接AE',AF',ET,
由题可得,点E关于直线AB的对称点为E',点F关于直线AD的对称点为F′,
∴B为EE'的中点,D为FF'的中点,
又∵四边形ABCD为正方形,
∴∠ABE=∠ADF=90°,
∴AB为EE'的中垂线,AD为FF'的中垂线,
∴AE=AE',AF=AF',
∵点P是EF的中点,
∴PE=PF,
又∵∠EPT=∠FPA,AP=TP,
∴△PET≌△PFA(SAS),
∴ET=AF,∠PET=∠PFA,
∴ET=AF',且∠AET=∠AEP+∠PET=∠AEP+∠AFP=180°﹣∠EAF,
∵AE'=AE,AB=AB,∠ABE'=∠ABE=90°,
∴Rt△ABE≌Rt△ABE'(HL),
∴∠BAE'=∠BAE,
同理可得∠FAD=∠F'AD,
∴∠E'AF'=∠BAE'+∠DAF'+∠BAD=∠BAE+∠DAF+∠BAD=(∠BAD﹣∠EAF)+∠BAD=180°﹣∠EAF,
∴∠AET=∠E'AF',
又∵AE'=AE,AF'=ET,
∴△E'AF'≌△AET(SAS),
∴E'F'=AT=2AP;
(3)解:如图③中,作ET∥BC,使得ET=MN=100米,延长ET交CD于点H,作点F关于BC的对称点F′,连接TF′交BC于点N,此时EM+MN+NF的值最小.
∵四边形ABCD是正方形,
∴AB=CD=BC=AD=800米,AD∥BC,
∵AE=EB,
∴DH=HC=400米,EH=AD=800米,
∴CF=CF′=300米,ET=MN=100米,
∴TH=700米,HF′=700米,
∴TF′===700=987(米),
∴EM+MN+NF=TN+ET+NF′=ET+TF′=1087米,
EM+MN+NF的最小值为1087米.
相关试卷
这是一份2024年中考数学专题训练 专题12 两之间线段最短求最值(四大类型含将军饮马)(知识解读),共27页。
这是一份2024年中考数学专题训练 专题02 二次函数与将军饮马最值问题(专项训练)(原卷版+解析),共14页。
这是一份2024年中考数学专题训练 专题11 利用垂线段最短求最值(三大类型含“胡不归”)(专项训练)(原卷版+解析),共21页。试卷主要包含了已知等内容,欢迎下载使用。










