2024年中考数学二轮专题提升训练：圆的综合

这是一份2024年中考数学二轮专题提升训练：圆的综合，共23页。

1．如图，⊙O是△ABC的外接圆，是的直径，为⊙O上一点，，垂足为，连接．
(1)求证：平分；
(2)当，时，求扇形的面积．
2．如图，为⊙O的直径，为⊙O上一点，连接，点是的中点，交的延长线于点，于点．
(1)求证：是⊙O的切线；
(2)若，，求⊙O的半径．
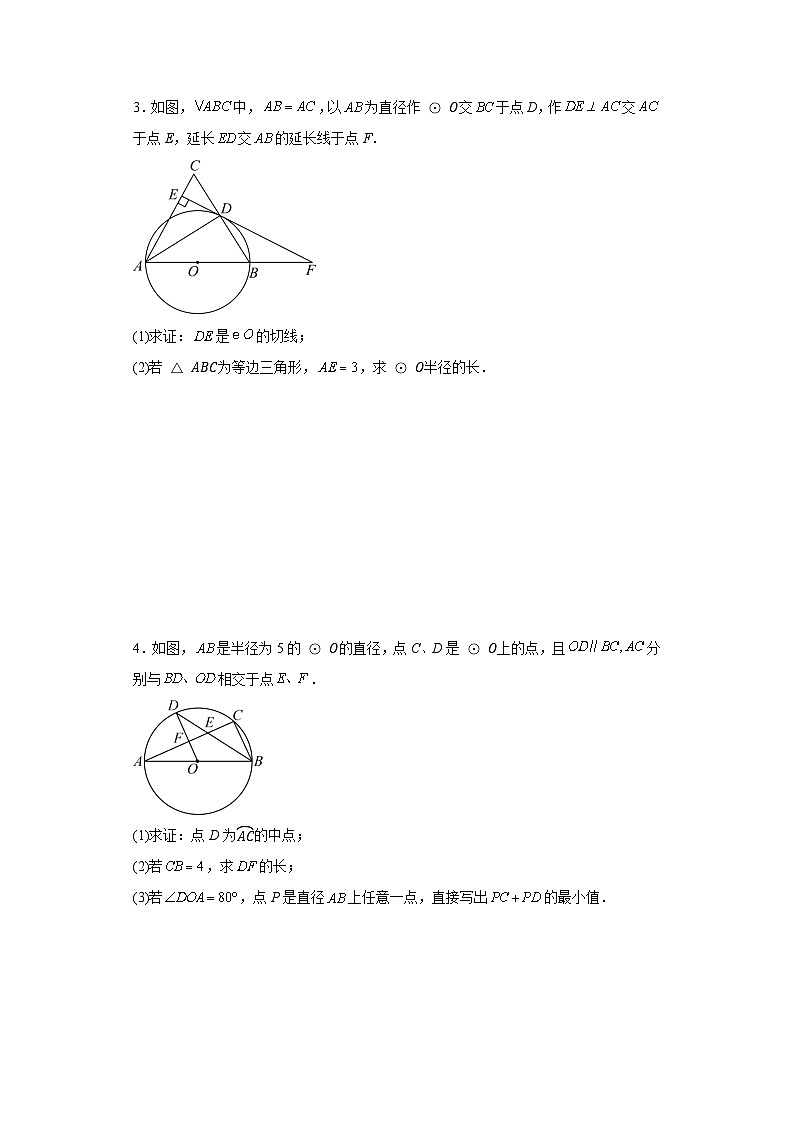
3．如图，中，，以为直径作⊙O交于点D，作交于点E，延长交的延长线于点F．

(1)求证：是的切线；
(2)若△ABC为等边三角形，，求⊙O半径的长．
4．如图，是半径为5的⊙O的直径，点C、D是⊙O上的点，且分别与相交于点．
(1)求证：点D为AC的中点；
(2)若，求的长；
(3)若，点P是直径上任意一点，直接写出的最小值．
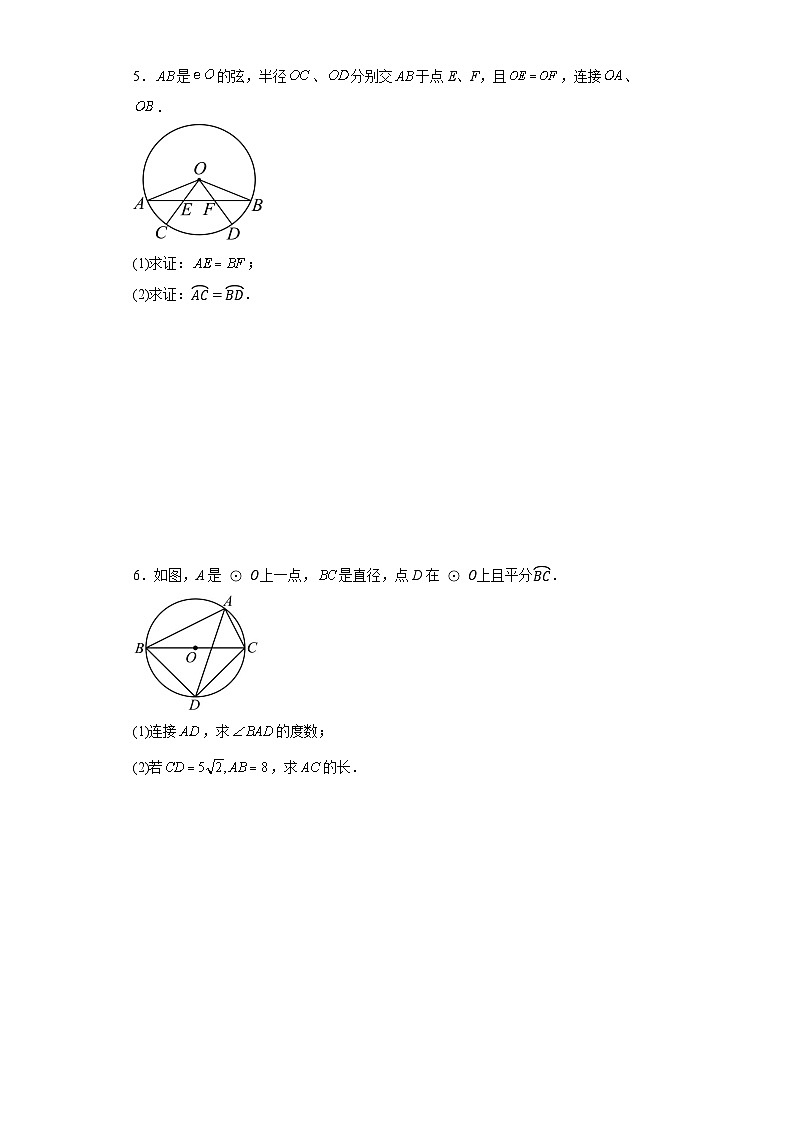
5．是的弦，半径、分别交于点E、F，且，连接、．
(1)求证：；
(2)求证：AC=BD．
6．如图，A是⊙O上一点，是直径，点D在⊙O上且平分BC．

(1)连接，求的度数；
(2)若，求的长．
7．如图，半圆中，点是BC的中点，点在直径上，且，半径交于点．
(1)求证：；
(2)若，，求的长．
8．如图，已知为的直径，是弦，于E，于F，连接，，.
(1)求证：；
(2)若cm，求的值及阴影部分的面积.
9．如图，是⊙O的直径，点D在的延长线上，与⊙O相切于点C．连接，．
(1)求证：；
(2)若，，求的长．
10．如图，A、P、B、C是⊙O上的四个点，，且平分．
(1)判断△ABC的形状，并证明你的结论；
(2)若⊙O的半径为2，求△ABC的面积．
11．如图，中，，点在边上，过点且分别与边、相交于、两点，，点为垂足．
(1)求证：直线是的切线；
(2)当是等边三角形，且直线与相切时，直接写出长度为线段长度2倍的所有线段．
12．如图1，是的直径，M是上一点．过点B作的垂线交射线于点C． 取的中点N，连结．
(1)求证：是的切线．
(2)如图2，连结，，若，求的值．
13．如图，矩形中，，．点是上的动点，以为直径的与交于点，过点作于点．
(1)当是的中点时：的值为 ；
(2)在（1）的条件下，证明：是的切线；
(3)试探究：能否与相切？若能，求出此时的长；若不能，请说明理由．
14．AB为⊙O的直径，弦CD⊥AB，垂足为H，F为弧BC上一点，且∠FBC＝∠ABC，连接DF，分别交BC、AB于E、G．
(1)如图1，求证：DF⊥BC；
(2)如图2，连接EH，过点E作EM⊥EH，EM交⊙O于点M，交AB于点N．
①求证：EN＝GN；
②连接OC，求证：△CHO≌△HEN．
15．如图1，在中，D在边上，圆O为锐角的外接圆，连接并延长交于点E，设．

(1)若，求的度数；
(2)如图2，作，垂足为F，与交于点G，已知．
①求证：；
②若，求的值．
参考答案：
1．（1）证明：∵，
∴，
∴，
∴平分
（2）解：∵，
∴
∴
∵
∴
2．1）证明：如图所示，连接．
∵点D是的中点，
∴，
∴，
∵，
∴．
∴．
∴．
∴．
∵，
∴．
∴．
∴．
又∵是半径，
∴是⊙O的切线．
（2）解：∵，，，
∴，
设的半径为r，则，
∴，
在中，由勾股定理得，
∴，
解得，
∴的半径为．
3．（1）证明：连接，
∵，
∴，
∵，

∴，
∴，
∴，
∵
∴，
∵是的半径，
∴是的切线；
（2）解：∵为等边三角形，
∴，
∵是的直径，
∴，
∴，，
∴，
∴，
∴，
∴
在中，，
∴
∴，
∴．
∴半径的长为2．
4．（1）证明：是的直径，
．
，
，
，
，
即点D是的中点．
（2）解：为的中点，
∴是的中位线，
．
又∵半径为5，
．
（3）解：作点C关于的对称点，即交于点P，连接，
．
，
此时的值最小，
，
，
．
∵点C与关于对称，
，
，．
作交于点H，
则，则，
在中，，
根据勾股定理，得，
，
的最小值为．
5．（1）证明：过O作于M，
（2）证明：，
，
，
6．（1）解：∵是直径，
∴，
∵点在上且平分，
，
；
（2）解：点D在上且平分，
，
，
，
，
．
7．（1）证明：如图，连接，交于点，
是半圆的直径，
，
，
是 的中点，是半径，
，
∴，
，
，
，
，
；
（2）解：，，
，，
，，
在中，，
是半径且，
，
在中，，
，
在中，．
8．（1）证明：∵，
∴，
∴，
∵，为的直径，
∴，
又∵，
∴；
（2）解：如图，连接．
∵，
∴点F是AC的中点，
∴是的中位线，
∴，
∵，
∴，，，
∴，
∴，
∴，
∴，，
∴，
∴．
9．（1）证明：连接，
∵与相切于C，
∴，
∴，
∴，
∵为的直径，
∴，
∴，
∴，
∵，
∴，
∴；
（2）解：在与中，
，
∴，
∴ ，
∵，
∴，
∴，
．
10．（1）为等边三角形，理由如下：
平分，，
，
，
为等边三角形；
（2）连接，并延长，交于点．
为等边三角形，
，
，
，
，
∵点在的垂直平分线上，
垂直平分，
，
，
，
．
11．1）证明：连接，如图，
，
．
，
，
，
．
，
，
为的半径，
直线是的切线；
（2）解：连接，如图，
为的直径，
，
是等边三角形，
，
，
．
，
，
．
直线与相切，
，
，
，
为等边三角形，
．
在和中，
，
，
．
同理：，
．
．
由题意：，
，
，
长度为线段长度2倍的所有线段有：，，，．
12．（1）证明：如图，连接，，
∵是的直径，
∴，
∵点N是的中点，
∴，
∴，
∵，
∴，
∴，
即，
∵，
∴，
∵是的半径，
∴是的切线；
（2）解：∵，
∴，
设，，
∴
∵，
∴，
∵，，
∴是的中位线，
∴，
∴．
13．（1）解：四边形是矩形，
，，，
，
是的中点，
，
．
故答案为：．
（2）证明：连接，
在矩形中，，，
又，
，
，
．
，
，
．
．
，
，
是的切线．
（3）解：若能与相切，由是的直径，则，．
设，则．
由勾股定理得：，
即，
整理得，
解得：，，
或9，
当时，，，
当时，，，
能与相切，此时或．
14．（1）证明：∵CD⊥AB，
∴∠BHC＝90°，
∴∠C+∠ABC＝90°，
∵∠FBC＝∠ABC，∠F＝∠C，
∴∠F+∠FBC＝90°，
∴∠BEF＝90°，
∴DF⊥BC．
（2）①证明：由（1）得∠CED＝∠BEF＝90°，
∵AB为⊙O的直径，弦CD⊥AB，
∴点H为CD的中点，
∴HE＝CD＝CH＝DH，
∴∠D＝∠HED，
∵EM⊥EH，
∴∠HED+∠DEN＝90°，
∵CD⊥AB，
∴∠D+∠DGH＝90°，
∴∠DEN＝∠DGH，
又∵∠DGH＝∠EGN，
∴∠DEN＝∠EGN，
∴EN＝GN；
②连接OC，
∵OC＝OB，
∴∠OCB＝∠OBC，
由①得∠DEN＝∠EGN，
∴∠BEN＝∠OBC，
∴∠OCB＝∠BEN，
∴∠COH＝∠HNE，
在△COH和△HNE中，
，
∴△COH≌△HNE（AAS）．
15．（1）如图，连接，

∵，
又∵，
∴，
∵，
∴；
（2）①证明：∵，
∴，
设，则，
由（1）得：，
∵，
∴，
∴，
∴；
②解：如图，作于点M，于点N，

由①得：，
∵
∴，
∴
∴，
∵
∴，
∴由勾股定理得，，
∵
∴四边形为矩形，
∴，
∵，
∴，
∴．