

02,浙江省杭州市文海中学2023-2024学年九年级上学期期中数学试题
展开答题时间120分钟 总分120分
一、选择题(每小题3分,共30分,每小题有四个选项,只有一个选项是正确的,请选出正确的选项)
1. 下列函数中,是二次函数的是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据二次函数的定义逐项判断即可.
【详解】A项,是二次函数,故本项符合题意;
B项,不是二次函数,故本项不符合题意;
C项,不是二次函数,故本项不符合题意;
D项,不是二次函数,故本项不符合题意;
故选:A.
【点睛】此题考查了二次函数的定义,熟记二次函数的定义及一般形式是解题的关键.二次函数的一般式是,其中 .
2. “清明时节雨纷纷”这个事件是( )
A. 必然事件B. 确定性事件C. 不可能事件D. 随机事件
【答案】D
【解析】
【分析】根据事件发生的可能性大小判断,即可得到答案.
【详解】解:“清明时节雨纷纷”这个事件是随机事件,
故选:D.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
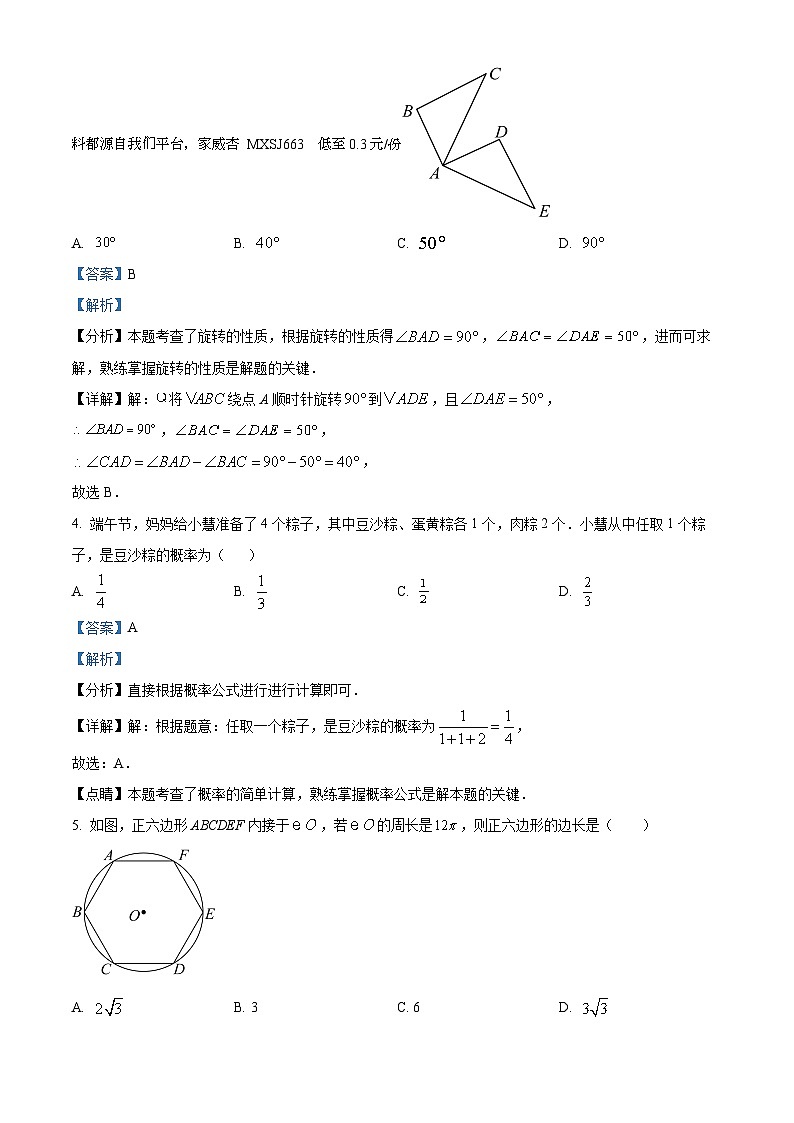
3. 如图将绕点A顺时针旋转到,若,则等于( )您看到的资料都源自我们平台,家威杏 MXSJ663 低至0.3元/份
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了旋转的性质,根据旋转的性质得,,进而可求解,熟练掌握旋转的性质是解题的关键.
【详解】解:将绕点A顺时针旋转到,且,
,,
,
故选B.
4. 端午节,妈妈给小慧准备了4个粽子,其中豆沙粽、蛋黄粽各1个,肉粽2个.小慧从中任取1个粽子,是豆沙粽的概率为( )
A. B. C. D.
【答案】A
【解析】
【分析】直接根据概率公式进行进行计算即可.
【详解】解:根据题意:任取一个粽子,是豆沙粽的概率为,
故选:A.
【点睛】本题考查了概率的简单计算,熟练掌握概率公式是解本题的关键.
5. 如图,正六边形ABCDEF内接于,若的周长是,则正六边形的边长是( )
A. B. 3C. 6D.
【答案】C
【解析】
【分析】如图所示,由正六边形ABCDEF内接于,可知是等边三角形,由的周长是,可得即可得出结果.
【详解】解:如图所示:
∵正六边形ABCDEF内接于,
是等边三角形,
∵的周长是,
故选:
【点睛】本题主要考查了圆内接正六边形的性质,等边三角形的判定及性质,正确运用圆与正六边形的性质是解此题的关键.
6. 如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )
A. 30°B. 40°C. 45°D. 50°
【答案】B
【解析】
【分析】首先根据等腰三角形性质及三角形内角和定理求出∠AOB的度数,再利用圆周角与圆心角的关系求出∠ACB的度数.
【详解】解:△AOB中,OA=OB,∠ABO=50°,
∴∠AOB=180°-2∠ABO=80°,
故选B.
【点睛】本题主要考查了圆周角定理应用,涉及到的知识点还有:等腰三角形的性质以及三角形内角和定理.
7. 如图,弦垂直平分半径,若的半径为2,则弦的长为( )
A. B. C. D.
【答案】D
【解析】
【分析】连接,先求解,再利用勾股定理求解,再利用垂径定理可得,从而可得答案.
【详解】解:连接,如图:
∵弦垂直平分半径,,
∴,,
在中,由勾股定理得:,
∴,
故选:D.
【点睛】本题考查的是勾股定理的应用,垂径定理,掌握以上知识是解题的关键.
8. 二次函数,当时,y随x的增大而减小,则实数a和t满足( )
A. ,B. ,C. ,D. ,
【答案】B
【解析】
【分析】首先根据题意得到二次函数的对称轴为,然后利用二次函数的性质求解即可.
【详解】∵二次函数,
∴对称轴为,
∵当时,y随x的增大而减小,
∴,.
故选:B.
【点睛】此题考查了二次函数的性质,解题的关键是熟练掌握二次函数的性质.
9. 一次综合实践的主题为:只用一张矩形纸条和刻度尺,如何测量一次性纸杯杯口的直径?小聪同学所在的学习小组想到了如下方法:如图,将纸条拉直紧贴杯口上,纸条的上下边沿分别与杯口相交于,,,四点,利用刻度尺量得该纸条宽为,,.请你帮忙计算纸杯的直径为( )
A. B. C. D.
【答案】B
【解析】
【分析】设圆心为O,根据垂径定理可以得到,,再根据勾股定理构建方程解题即可.
【详解】设圆心为O,为纸条宽,连接,,
则,,
∴,,
设,则,
又∵,
∴,即,
解得:,
∴半径,
即直径为,
故选B.
【点睛】本题考查垂径定理,勾股定理,构建直角三角形利用勾股定理计算是解题的关键.
10. 在平面直角坐标系中,抛物线与x轴交于,两点,其中,将此抛物线向上平移,与x轴交于,两点,其中,下面结论正确的是( )
A. 当时,
B. 当时,
C. 当时,
D. 当时,
【答案】A
【解析】
【分析】本题考查二次函数的性质和平移,分情况讨论:或,根据抛物线与x轴两交点关于对称轴对称,故得到交点横坐标之间的关系.由对称轴得到抛物线与x轴交点的横坐标之间的数量关系是解题的关键.
【详解】当时,如图所示:
由图象可得,
∵抛物线,
∴抛物线的对称轴为直线,
∴,
由∵,
∴,,
当时,如图所示:
由图象可得,
∵抛物线
∴抛物线的对称轴为直线,
∴,.
故选:A.
二、填空题(每小题4分,共24分)
11. 抛物线经过点,是__________.
【答案】
【解析】
【分析】把点的坐标代入抛物线即可得到答案,熟练掌握抛物线上的点满足函数表达式是解题的关键.
【详解】解:∵抛物线经过点,
∴,
故答案为:
12. 一个仅装有球的不透明布袋里只有6个红球和个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则_________.
【答案】9
【解析】
【分析】根据概率公式列分式方程,解方程即可.
【详解】解:从中任意摸出一个球是红球的概率为,
,
去分母,得,
解得,
经检验是所列分式方程的根,
,
故答案为:9.
【点睛】本题考查已知概率求数量、解分式方程,解题的关键是掌握概率公式.
13. 如图,中,弦,相交于点P,,,则__________度.
【答案】
【解析】
【分析】此题主要考查了圆周角定理,根据三角形外角的性质可求出,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等可得答案.关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
【详解】解:∵,,
∴,
∵,
∴.
故答案为:.
14. 公园草坪上,自动浇水喷头喷出的水线呈一条抛物线,水线上水珠的高度(米)关于水珠与喷头的水平距离(米)的函数解析式是.水珠可以达到的最大高度是__________米.
【答案】14
【解析】
【分析】本题考查了二次函数的应用,根据二次函数的顶点式即可求解.解决本题的关键是掌握把二次函数的解析式化为顶点式.
【详解】∵,
∴时,y取最大值,
∴水珠可以达到的最大高度是14米.
故答案为:14.
15. 如图,是半圆的直径,,是半圆弧的三等分点,于点,连接,若,则图中阴影部分的面积为 ______ .
【答案】
【解析】
【分析】过点作,连接,,,分别求出扇形和三角形的面积,即可求出阴影部分的面积.
【详解】过点D作,连接,,,
∵,
∴,
∵是半圆的直径,,是半圆弧的三等分点,
∴,
∴,
∴,
∵,,
∴,
∵是半圆的直径,,是半圆弧的三等分点,
∴,
∴,
∵,,
∴,
∴,
∴图中阴影部分的面积为:.
故答案为:.
【点睛】本题考查不规则图形的面积,解题的关键是作出辅助线,将不规则图形的面积转化为规则图形的面积.
16. 如图,以为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆G上一动点,于F.
(1)的长度为__________;
(2)当点E在圆G的运动过程中,线段的长度的最小值为__________.
【答案】 ①. ②.
【解析】
【分析】(1)连接,作,连接,由垂径定理得到,由为圆心,半径为4,得到,在中,,,,,则,,即可得到,则,由弧长公式得到的长度为;
(2)由可知,点F在以为直径的圆M上移动,当点F在的延长线上时,的长最小,根据含30度角的直角三角形的性质及勾股定理求出,即可解答.
【详解】解:(1)连接,作,连接,
∵,
∴,
∵为圆心,半径为4,
∴,
在中,,,
∴,,
∵,
∴,
∵,
∴,
∴,
∴的长度为,
(2)∵,
∴,
∵,
∴点F在以为直径的圆M上移动,
当点F在的延长线上时,的长最小,最小值为,
故答案为;.
【点睛】此题考查了垂径定理、圆周角定理、等腰三角形的判定和性质、度角的直角三角形的性质、勾股定理、弧长公式等知识,解题的关键是学会添加常用的辅助线解决问题.
三、解答题(共8小题,总分66分)
17. 已知,求的值.
【答案】
【解析】
【分析】根据比例的基本性质得到,整理得到,即可得到的值,此题考查了比例的基本性质,熟练掌握比例式的外项之积等于内项之积是解题的关键.
【详解】解:∵,
∴,
∴,
∴.
18. 如图,在中,.
(1)作的外接圆(要求尺规作图,并保留作图痕迹);
(2)求此外接圆半径.
【答案】(1)见解析 (2)
【解析】
【分析】(1)分别作和的中垂线,它们的交点O就是圆心,连接,以点O为圆心,为半径画圆即可;
(2)连接,根据的度数以及等腰三角形的性质得出为等边三角形,然后求出半径即可.
【小问1详解】
如图所示:即为所求的的外接圆;
【小问2详解】
连接,
∵,
∴,
∴
∵,
∴是等边三角形,
∴,
即它的外接圆半径为.
【点睛】此题考查了三角形外接圆的作法、等边三角形的判定与性质、等腰三角形的性质、圆周角定理等知识,准确作图是解题的关键.
19. 如图,已知二次函数图象经过点和.
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当时,请根据图象直接写出x的取值范围.
【答案】(1)二次函数的表达式为,顶点坐标为
(2)
【解析】
【分析】本题考查的是利用待定系数法求解二次函数的解析式,二次函数的顶点坐标,利用图象法解不等式,
(1)把和代入,建立方程组求解解析式即可,再把解析式化为顶点式,可得顶点坐标;
(2)把代入函数解析式求解的值,再利用函数图象可得时的取值范围.
熟练的运用数形结合的方法解题是关键.
【小问1详解】
解:∵二次函数图象经过点和.
∴,解得:,
∴抛物线为,
∴顶点坐标为:;
【小问2详解】
当时,,
∴
解得:,,
如图所示,
∴当时,.
20. 第19届亚运会于2023年9月23日至10月8日在杭州举行,杭州亚运会吉祥物是“宸宸”“琮琮”和“莲莲”,将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.
(1)若从中任意抽取1张,抽得卡片上的图案恰好为“琮琮”的概率是________;
(2)若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片图案相同的概率.(请用树状图或列表的方法求解)
【答案】(1)
(2)
【解析】
【分析】本题主要考查列表或画树状图求随机事件的概率,掌握列表或树状图计算随机事件的概率的方法是解题的关键.
(1)根据概率的计算公式即可求解;
(2)运用列表或画树状图把所有等可能结果表示出来,再根据概率的计算方法即可求解.
【小问1详解】
解:从中任意抽取1张,抽得卡片上的图案恰好为“琮琮”的概率是,
故答案为:;
【小问2详解】
把吉祥物“宸宸”、“琮琮”、“莲莲”三张卡片分别记为A、B、C,
画树状图如图:
共有9种等可能的结果,两次抽取的卡片图案相同的结果有3种,
∴两次抽取的卡片图案相同的概率为.
21. 如图,是的直径,是的一条弦,且于点E.
(1)求证:;
(2)若,求阴影部分面积.
【答案】(1)见解析 (2)
【解析】
【分析】(1)由等边对等角可得,再根据同弧所对的圆周角相等可得,最后根据等量代换即可解答;
(2)根据垂径定理可得,设的半径为r,则,结合可得,最后在中运用勾股定理列式计算即可求出的半径为4,再利用三角函数求出,再利用即可求出答案.
小问1详解】
证明:∵,
∴,
∵,
∴.
【小问2详解】
解:∵是的直径,且于点E,,
∴.
设的半径为r,则,.
∵,
∴.
在中,,
∴,
解得,
∴,,
∴,
∴,
∴.
【点睛】本题主要考查了等腰三角形的性质、圆周角定理、垂径定理、勾股定理、锐角三角形函数、扇形面积公式等知识点,灵活运用相关性质和定理成为解答本题的关键.
22. 小明的妈妈创办了一个微店商铺,营销一款儿童玩具,成本是20元/个,在“双十一”前20天进行了网上销售后发现,该玩具的日销售量p(个)与时间x(天)之间满足一次函数关系,且第1天销售了78个,第4天销售了72个.该玩具的销售价格y(元/个)与时间x(天)之间符合函数关系式(,且x为整数).
(1)求日销售量p(个)与时间x(天)之间的函数关系式,
(2)在这20天中,哪天的日销售利润最大?最大日销售利润是多少?
【答案】(1)
(2)第10日销售利润最大,最大日销售利润是450元
【解析】
【分析】本题考查了一次函数、二次函数的应用,
(1)设日销售量(盒与时间(天之间的函数关系式为,把,代入求出即可;
(2)设日销售利润为元,根据销售利润售价成本列出函数解析式,再根据函数的性质求最值;
主要考查学生能否把实际问题转化成数学问题,根据数量关系列出函数解析式是关键.
【小问1详解】
解:设日销售量(盏与时间(天之间函数关系式为,
把,代入得:,
解得:,
即日销售量(盏与时间(天之间的函数关系式为;
【小问2详解】
解:设日销售利润为元,
;
,,且为整数,
当时,取得最大值,最大值是450;
在这20天中,第10日销售利润最大,最大日销售利润是450元.
23. 在平面直角坐标系中,已知抛物线.
(1)若抛物线过点,求该抛物线的解析式
(2)当时,y的最小值是,则当时,求y的最大值.
(3)已知直线与抛物线存在两个交点,若两交点到x轴的距离相等,求a的值.
【答案】23.
24. 或
25.
【解析】
【分析】(1)把点代入得,求出的值即可;
(2)求出抛物线的对称轴为直线,可知顶点的纵坐标就是的最小值,分和,由此求出抛物线的解析式,再由二次函数的性质求出的最大值即可;
(3)由直线与抛物线存在两个交点,,且,即一元二次方程有两个不相等的实数根,则,,得到,由两交点到x轴的距离相等得到,即,解得.
【小问1详解】
解:把点代入,
得,
解得:,
该抛物线的解析式为:;
【小问2详解】
解:,
抛物线的对称轴为直线,
当时;
当时,的最小值是,
当时,,
解得:,
抛物线的解析式为:,
当时,随的增大而减小,当时,,
当时,随的增大而增大,当时,,
当时,∵时,的最小值是,抛物线的对称轴为直线,
∴当时,,将代入,
即,
解得:,
∴当时取得最大值,最大值为,
综上所述,当时,的最大值为或;
【小问3详解】
解:∵直线与抛物线存在两个交点,,且,
∴,即一元二次方程有两个不相等的实数根,,
则,,
,
∵两交点到x轴的距离相等,
∴,
∴,
即,
∴,
∴,
解得.
【点睛】本题考查了待定系数法求二次函数的解析式、二次函数和一次函数的交点问题、二次函数的图象与性质、一元二次方程的根的判别式和根与系数关系、分式方程等知识,熟练掌握二次函数的图象与性质是解此题的关键.
24. 如图,AB为⊙O的直径,点D为AB下方⊙O上一点,点C为弧ABD的中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长度.
【答案】(1)证明见解析;(2)见解析;(3).
【解析】
【分析】(1)连接AD,如图1,设∠BDC=α,∠ADC=β,根据圆周角定理得到∠CAB=∠BDC=α,由AB为⊙O直径,得到∠ADB=90°,根据余角的性质即可得到结论;
(2)根据已知条件得到∠ACE=∠ADC,等量代换得到∠ACE=∠CAE,于是得到结论;
(3)如图2,连接OC,根据圆周角定理得到∠COB=2∠CAB,等量代换得到∠COB=∠ABD,根据相似三角形的性质得到OH=5,根据勾股定理得到AB==26,由相似三角形的性质即可得到结论.
【详解】(1)连接AD.如图1,设∠BDC=α,∠ADC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,∴=,∴∠ADC=∠DAC=β,∴∠DAB=β﹣α,
∵AB为⊙O直径,∴∠ADB=90°,∴α+β=90°,∴β=90°﹣α,∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),∴∠ABD=2α,∴∠ABD=2∠BDC;
(2)∵CH⊥AB,∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,∴∠ACE=∠ADC,
∵∠CAE=∠ADC,∴∠ACE=∠CAE,∴AE=CE;
(3)如图2,连接OC,∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,∴△OCH∽△ABD,∴,
∵OH=5,∴BD=10,∴AB==26,∴AO=13,∴AH=18,
∵△AHE∽△ADB,∴,即=,∴AE=,∴DE=.
【点睛】本题考查了垂径定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.
2023-2024学年浙江省杭州市上城区开元中学九年级上学期期中数学试题: 这是一份2023-2024学年浙江省杭州市上城区开元中学九年级上学期期中数学试题,文件包含浙江省杭州市上城区开元中学九年级上学期期中数学试题原卷版docx、浙江省杭州市上城区开元中学九年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
浙江省杭州市2023-2024学年九年级上学期期中数学试题(含解析): 这是一份浙江省杭州市2023-2024学年九年级上学期期中数学试题(含解析),共22页。试卷主要包含了选择题等内容,欢迎下载使用。
浙江省杭州市拱墅区文澜中学2023-2024学年七年级上学期期中数学试题(无答案): 这是一份浙江省杭州市拱墅区文澜中学2023-2024学年七年级上学期期中数学试题(无答案),共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












