


- 专题14 全等与相似模型-一线三等角(K字)模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用) 试卷 0 次下载
- 专题15 全等与相似模型-手拉手模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用) 试卷 1 次下载
- 专题17 全等与相似模型-对角互补模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用) 试卷 0 次下载
- 专题18 全等与相似模型之十字模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用) 试卷 1 次下载
- 专题19 相似三角形重要模型之(双)A字型与(双)8字型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用) 试卷 0 次下载
专题16 全等与相似模型-半角模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用)
展开模型1.半角模型
半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半。
思想方法:通过旋转(或截长补短)构造全等三角形,实现线段的转化。
解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论。
【模型展示】
1)正方形半角模型
条件:四边形ABCD是正方形,∠ECF=45°;
结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④AEF的周长=2AB;
⑤CE、CF分别平分∠BEF和∠EFD。
2)等腰直角三角形半角模型
条件:ABC是等腰直角三角形,∠DAE=45°;
结论:①△BAD≌△CAG;②△DAE≌△GAE;③∠ECG==90°;④DE2=BD2+EC2;
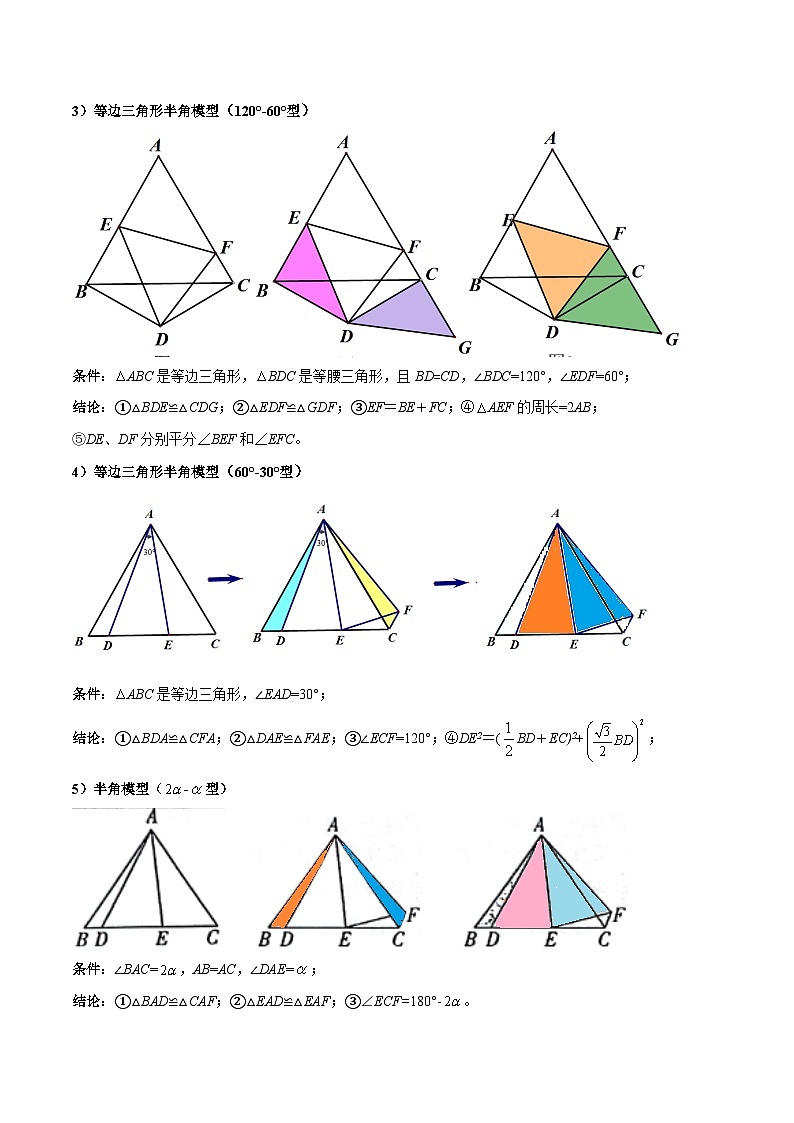
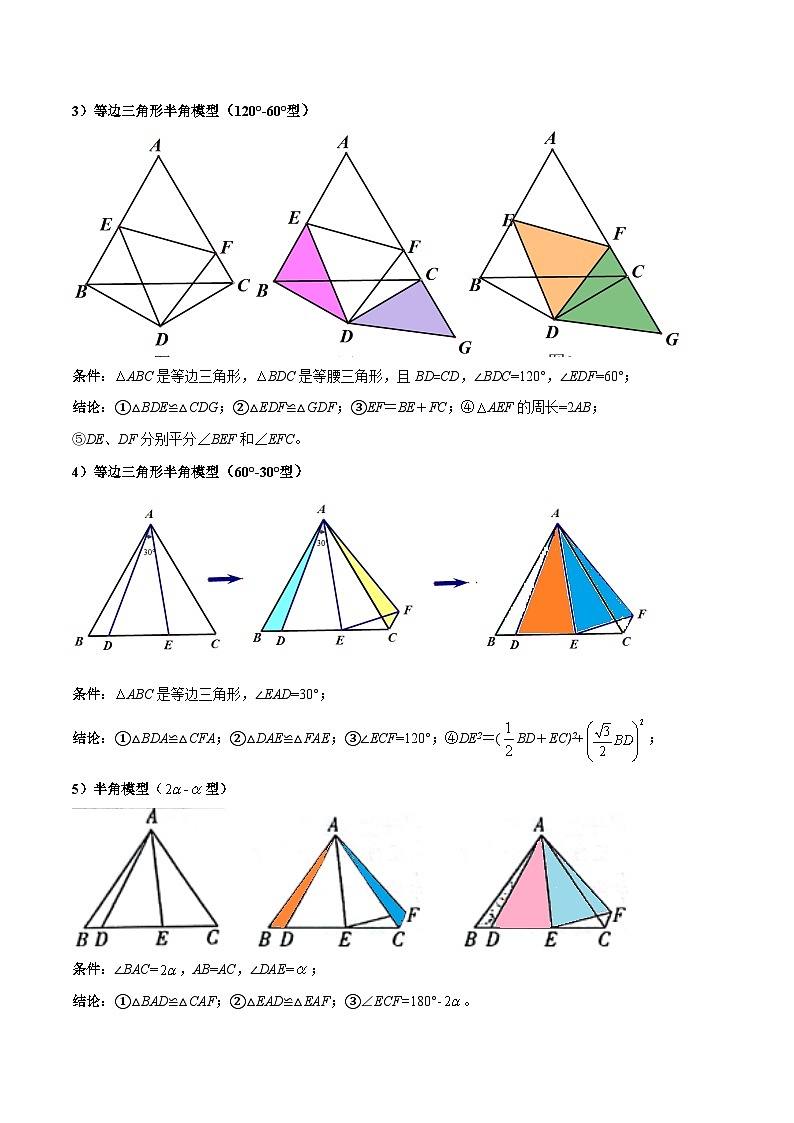
3)等边三角形半角模型(120°-60°型)
条件:ABC是等边三角形,BDC是等腰三角形,且BD=CD,∠BDC=120°,∠EDF=60°;
结论:①△BDE≌△CDG;②△EDF≌△GDF;③EF=BE+FC;④AEF的周长=2AB;
⑤DE、DF分别平分∠BEF和∠EFC。
4)等边三角形半角模型(60°-30°型)
条件:ABC是等边三角形,∠EAD=30°;
结论:①△BDA≌△CFA;②△DAE≌△FAE;③∠ECF=120°;④DE2=(BD+EC)2+;
5)半角模型(-型)
条件:∠BAC=,AB=AC,∠DAE=;
结论:①△BAD≌△CAF;②△EAD≌△EAF;③∠ECF=180°-。
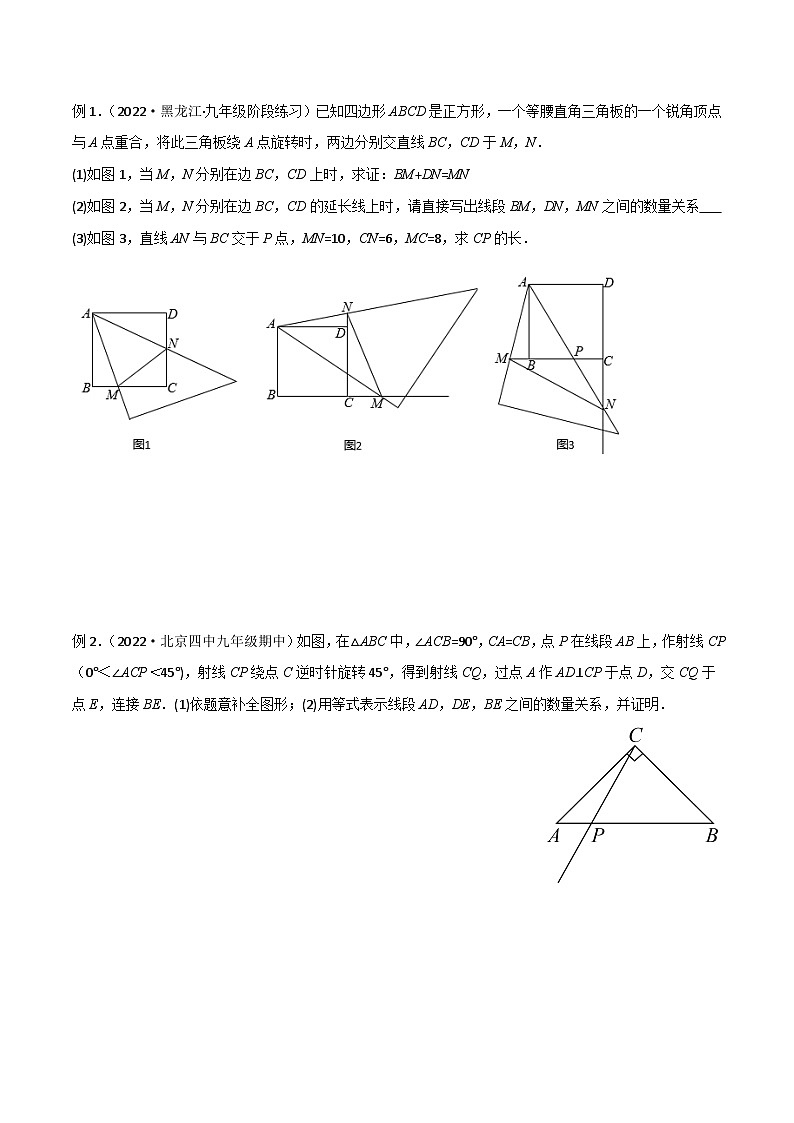
例1.(2022·黑龙江·九年级阶段练习)已知四边形ABCD是正方形,一个等腰直角三角板的一个锐角顶点与A点重合,将此三角板绕A点旋转时,两边分别交直线BC,CD于M,N.
(1)如图1,当M,N分别在边BC,CD上时,求证:BM+DN=MN
(2)如图2,当M,N分别在边BC,CD的延长线上时,请直接写出线段BM,DN,MN之间的数量关系
(3)如图3,直线AN与BC交于P点,MN=10,CN=6,MC=8,求CP的长.
【答案】(1)见解析;(2);(3)3
【分析】(1)延长到使,连接AG,先证明,由此得到,,再根据,,可以得到,从而证明,然后根据全等三角形的性质即可证明;(2)在BM上取一点G,使得,连接AG,先证明,由此得到,,由此可得,再根据可以得到,从而证明,然后根据全等三角形的性质即可证明;(3)在DN上取一点G,使得,连接AG,先证明,再证明,设,根据可求得,由此可得,最后再证明,由此即可求得答案.
【详解】(1)证明:如图,延长到使,连接AG,
∵四边形ABCD是正方形,∴,,
在与中,, ,,,
,,∴,
,,
在与中,, ,,
又∵,,;
(2),理由如下:如图,在BM上取一点G,使得,连接AG,
∵四边形ABCD是正方形,∴,,
在与中,, ,,,
∴,∴,
又,,
在与中,, ,,
又∵,,∴,故答案为:;
(3)如图,在DN上取一点G,使得,连接AG,
∵四边形ABCD是正方形,∴,,,
在与中,, ,
,,∴,∴,
又,,
在与中,, ,,
设,∵,,∴,,
∵,∴,解得:,∴,∵,∴,
在与中,, ,,∴CP的长为3.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,能够作出正确的辅助线并能灵活运用全等三角形的判定与性质是解决本题的的关键.
例2.(2022·北京四中九年级期中)如图,在△ABC中,∠ACB=90°,CA=CB,点P在线段AB上,作射线CP(0°<∠ACP<45°),射线CP绕点C逆时针旋转45°,得到射线CQ,过点A作AD⊥CP于点D,交CQ于点E,连接BE.(1)依题意补全图形;(2)用等式表示线段AD,DE,BE之间的数量关系,并证明.
【答案】(1)作图见解析.(2)结论:AD+BE=DE.证明见解析.
【分析】(1)根据要求作出图形即可.(2)结论:AD+BE=DE.延长DA至F,使DF=DE,连接CF.利用全等三角形的性质解决问题即可.
(1)解:如图所示:
(2)结论:AD+BE=DE.
理由:延长DA至F,使DF=DE,连接CF.∵AD⊥CP,DF=DE,∴CE=CF,∴∠DCF=∠DCE=45°,
∵∠ACB=90°,∴∠ACD+∠ECB=45°,∵∠DCA+∠ACF=∠DCF=45°,∴∠FCA=∠ECB,
在△ACF和△BCE中,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=DE.
【点睛】本题考查作图-旋转变换,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
例3.(2022秋·江苏扬州·八年级校考阶段练习)如图,在等边三角形中,在AC边上取两点使.若,,, 则以为边长的三角形的形状为( )
A.锐角三角形B.直角三角形C.钝角三角形D.随的值而定
【答案】C
【分析】将△ABM绕点B顺时针旋转60°得到△CBH,连接HN,根据等边三角形的性质及各角之间的等量关系可得:∠NBM=∠NBH,然后依据全等三角形的判定定理可得△NBM≌△NBH,由全等三角形的性质可将x、m、n放在△NCH中,即可确定三角形的形状.
【详解】解:如图所示:将△ABM绕点B顺时针旋转60°得到△CBH,连接HN,
由旋转性质可知,BM=BH,CH=AM,,,
∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°,∵∠MBN=30°,∴∠ABM+∠CBN=30°,
∴∠NBH=∠CBH+∠CBN=∠ABM+∠CBN =30°,∴∠NBM=∠NBH,
在△NBM与△NBH中,,∴△NBM≌△NBH(SAS),∴MN=NH=x,
∵∠BCH=∠A=60°,CH=AM=m,∴∠NCH=120°,
∴以x,m,n为边长的三角形△NCH是钝角三角形.故选:C.
【点睛】本题考查等边三角形的性质、全等三角形的判定和性质、旋转变换等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,
例4.(2022·广东深圳·八年级期末)如图,△ABC中,∠BAC=120°,AB=AC,点D为BC边上一点.点E为线段CD上一点,且CE=2,AB=,∠DAE=60°,则DE的长为 ______.
【答案】
【分析】将绕点A逆时针旋转至,连接ME,过M作于Q,过A作 于F,由旋转的性质得,设,则 ,,证明,得,最后利用勾股定理来解答.
【详解】解:如图,将绕点A逆时针旋转至,连接ME,过M作于Q,过A作 于F,
∵,,,AB=,
∴,, ∴,,
∴,.
在中,.∵,∴.
设,∴ ,,∴.
∵,,∴,∴.
∵.在和中,∴,
∴,由勾股定理得:,
∴,∴,即 .故答案为:.
【点睛】本题考查含30°角的直角三角形的性质,等腰三角形的性质,全等三角形有判定和性质,勾股定理,旋转的性质,作辅助线构造直角三角形是求解本题的关键.
例5.(2022·广东广州·二模)如图,点为等边外一点,,,点,分别在和上,且,,,则的边长为______.
【答案】
【分析】先证明∠DBM=∠DCN=90°,如图,延长AC至H,使CH=BM,连接DH,再证明△DBM≌△DCH(SAS), 证明△MDN≌△HDN(SAS),可得MN=HN=BM+CN,从而可得答案.
【详解】解:∵△ABC为等边三角形∴∠ABC=∠ACB=60°,
∵∠BDC=120°,BD=CD, ∴∠DBC=∠DCB=×(180°-120°)=30°, ∴∠DBM=∠DCN=90°,
如图,延长AC至H,使CH=BM,连接DH,
∴∠DCH=90°, ∴∠DBM=∠DCH,
在△DBM和△DCH中,, ∴△DBM≌△DCH(SAS), ∴DM=DH,∠BDM=∠CDH,
∵∠BDM+∠CDN=60°, ∴∠CDN+∠CDH=60°, ∴∠MDN=∠HDN,
在△MDN和△HDN中,, ∴△MDN≌△HDN(SAS),∴MN=HN=BM+CN,
,,,
即等边三角形的边长为: 故答案为:
【点睛】本题考查的是等边三角形的性质,全等三角形的判定与性质,作出适当的辅助线构建全等三角形是解本题的关键.
例6.(2023春·江苏·八年级专题练习)(1)如图①,在四边形中,,,,分别是边,上的点,且.请直接写出线段,,之间的数量关系:___________;
(2)如图②,在四边形中,,,,分别是边,上的点,且,(1)中的结论是否仍然成立?请写出证明过程;
(3)在四边形中,,,,分别是边,所在直线上的点,且.请画出图形(除图②外),并直接写出线段,,之间的数量关系.
【答案】(1);(2)成立,理由见解析;(3)图形见解析,
【分析】(1)延长到,使,连接.证明,则,,,证明,得出,由此可得,;
(2)思路和作辅助线的方法同(1);
(3)根据(1)的证法,可得出,,那么.
【详解】解:(1)延长至,使,连接,
∵,,,∴,
∴,,∴,∴,
在和中,∵,∴,∴,
∵,且∴,故答案为:.
()解:()中的结论仍成立,证明:如图所示,延长至,使,
∵,,∴,
在和中,,∴,∴,,
∵,∴,∴,即,
在和中,,∴,
∴,即.
(),证明:如图所示,在上截取使,连接,
∵,,∴,
在和中,,∴,
∴,,∴,∴,
在和中, ,∴,∴,
∵,且,∴.
【点睛】此题主要考查了三角形全等的判定与性质,通过全等三角形来实现线段的转换是解题关键,没有明确的全等三角形时,要通过辅助线来构建与已知和所求条件相关联的全等三角形.
例6.(2023.山东八年级期中)综合与实践
(1)如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,则MN,AM,CN的数量关系为 .(2)如图2,在四边形ABCD中,BC∥AD,AB=BC,∠A+∠C=180°,点M、N分别在AD、CD上,若∠MBN=∠ABC,试探索线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
(3)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=∠ABC,试探究线段MN、AM、CN的数量关系为 .
【答案】(1)MN=AM+CN;(2)MN=AM+CN,理由见解析;(3)MN=CN-AM,理由见解析
【详解】解:(1)如图,把△ABM绕点B顺时针旋转使AB边与BC边重合,则AM=CM',BM=BM',∠A=∠BCM',∠ABM=∠M'BC,
在正方形ABCD中,∠A=∠BCD=∠ABC=90°,AB=BC ,∴∠BCM'+∠BCD=180°,
∴点M'、C、N三点共线,∵∠MBN=45°,∴∠ABM+∠CBN=45°,
∴∠M'BN=∠M'BC+∠CBN=∠ABM+∠CBN=45°,即∠M'BN=∠MBN,
∵BN=BN,∴△NBM≌△NBM',∴MN= M'N,∵M'N= M'C+CN,∴MN= M'C+CN=AM+CN;
(2)MN=AM+CN;理由如下:
如图,把△ABM绕点B顺时针旋转使AB边与BC边重合,则AM=CM',BM=BM',∠A=∠BCM',∠ABM=∠M'BC,
∵∠A+∠C=180°,∴∠BCM'+∠BCD=180°,∴点M'、C、N三点共线,
∵∠MBN=∠ABC,∴∠ABM+∠CBN=∠ABC=∠MBN,∴∠CBN+∠M'BC =∠MBN,即∠M'BN=∠MBN,
∵BN=BN,∴△NBM≌△NBM',∴MN= M'N,∵M'N= M'C+CN,∴MN= M'C+CN=AM+CN;
(3)MN=CN-AM,理由如下:如图,在NC上截取C M'=AM,连接B M',
∵在四边形ABCD中,∠ABC+∠ADC=180°,∴∠C+∠BAD=180°,
∵∠BAM+∠BAD=180°,∴∠BAM=∠C,∵AB=BC,∴△ABM≌△CB M',
∴AM=C M',BM=B M',∠ABM=∠CB M',∴∠MA M'=∠ABC,
∵∠MBN=∠ABC,∴∠MBN=∠MA M'=∠M'BN,∵BN=BN,∴△NBM≌△NBM',∴MN= M'N,
∵M'N=CN-C M', ∴MN=CN-AM.故答案是:MN=CN-AM.
模型2.半角模型(相似模型)
【常见模型及结论】
1)半角模型(正方形中的半角相似模型)
条件:已知,如图,在正方形ABCD中,∠EAF的两边分别交BC、CD边于M、N两点,且∠EAF=45°
结论:如图1,△AMN∽△AFE且.(思路提示:∠ANM=∠AEF,∠AMN=∠AFE);
图1 图2
结论:如图2,△MAN∽△MDA,△NAM∽△NBA;
结论:如图3,连接AC,则△AMB∽△AFC,△AND∽△AEC.且;
图3 图4
结论:如图4,△BME∽△AMN∽△DFN.
2)半角模型(特殊三角形中的半角相似模型)
(1)含45°半角模型
图1 图2
条件:如图1,已知∠BAC=90°,;
结论:①△ABE∽△DAE∽△DCA;②;③ ()
(2)含60°半角模型
条件:如图1,已知∠BAC=120°,;
结论:①△ABD∽△CAE∽△CBA;②;③ ()
例1.(2023·山东济南·九年级期中)如图,在正方形中,点E、F分别是、边上的两点,且,、分别交于M,N.下列结论:①;②平分;③;④.其中正确的结论是( )
A.①②③④B.①②③C.①③D.①②
【答案】A
【分析】①转证AB:BN=DM:AB,因为AB=AD,所以即证AB:BN=DM:AD.证明△ABN∽△MDA;②把△ABE绕点A逆时针旋转90°,得△ADH证明△AFH≌△AFE(SAS);③即证AM:AN=AF:AE,证明△AMN∽△AFE(两角相等);④由②得BE十DF=EF,当E点与B点重合、F与C重合时,根据正方形的性质,结论成立.
【详解】①∠BAN=∠BAM+∠MAN=∠BAM+45°,
∠AMD=∠ABM+∠BAM=45°+∠BAM,∠BAN=∠AMD.
又∠ABN=∠ADM=45°,△ABN∽△MDA,AB:BN=DM:AD,
AD=AB,.故①正确;
②如图,把△ABE绕点A逆时针旋转90°,得到△ADH,
∠BAD=90°,∠EAF=45°,∠BAE+∠DAF=45°.∠EAF=∠HAF,
AE=AH,AF=AF,△AEF≌△AHF,
∠AFH=∠AFE,即AF平分∠DFE,故②正确;
③AB∥CD,∠DFA=∠BAN,
∠AFE=∠AFD,∠BAN=∠AMD,∠AFE=∠AMN,
又∠MAN=∠FAE,△AMN∽△AFE,
AM:AF=AN:AE,即AM·AE=AN·AF,故③正确;
④由②得BE+DF=DH+DF=FH=FE,过A作AO⊥BD,作AG⊥EF,
则△AFE与△AMN的相似比就是AG:AO,易证△ADF≌△AGF(AAS),
则可知,从而得证,故④正确,故选:A .
【点睛】此题考查了正方形的性质、相似(包括全等)三角形的判定和性质、旋转的性质等知识点,综合性极强,难度较大.
例2.(2023·山西晋城·校联考模拟预测)如图,在矩形中,,,,分别为,边上的点.若,,则的长为 .
【答案】3
【分析】先做辅助线,作出相似三角形,再用等腰直角三角形的性质,相似的判定和性质即可求得的长.
【详解】在上作点G,使,在上作点H,使,
∵∴
又∵∴,∴
设,则 同理可得,
∴∴
∵
∴
∵,∴∴∴∴∴故填:3
【点睛】本题考查了矩形的性质,等腰直角三角形的性质,相似的判定与性质,严格的逻辑思维时解题的关键,做辅助线时解题的难点.
例3.(2023秋·江苏泰州·九年级统考期末)如图,已知中,,,点、在边上,.(1)求证:;(2)当,时,求的长.
【答案】(1)见解析(2)
【分析】(1)根据已知条件得出,,又,根据两边成比例夹角相等证明,根据相似三角形的性质即可得证;
(2)过点作于点,勾股定理求得,由(1)可知,根据相似三角形的性质列出比例式,进而即可求解.
【详解】(1)证明:∵,,∴
∵∴,又∵,∴,
∴,即;
(2)解:如图,过点作于点,∴,
∵,∴是等腰直角三角形,
∵,,∴
∵,∴,,,
∵,∴,在中,,
由(1)可知∴,
设,∴解得:,∴.
【点睛】本题考查了相似三角形的性质与判定,掌握相似三角形的性质与判定是解题的关键.
例4.(2023·江苏无锡·九年级期中)如图,在中,,,点D、E都在边上,.若,则的长为 .
【答案】/
【分析】将绕点A逆时针旋转120°得到,取的中点G,连接、,由,,可得出,根据旋转的性质可得出,结合可得出为等边三角形,进而得出为直角三角形,求出的长度以及证明全等找出,设,则,在中利用勾股定理可得出,利用可求出x以及的值,此题得解.
【详解】解:将绕点A逆时针旋转120°得到,取的中点G,连接、,如图所示:
过点A作于点N,如图,
∵,,∴,.
在中,,,∴,
∴,∴.∴,∴.
∵,∴,∴为等边三角形,
∴,∴,∴为直角三角形.
∵,∴,
∴.
在和中,,∴,∴.
设,则,
在中,,,
∴,∴,∴.故答案为:.
【点睛】本题考查了全等三角形的判定与性质、勾股定理、旋转的性质,通过勾股定理找出关于x的方程是解题的关键.
例5.(2023秋·江苏泰州·九年级校考期末)(1)如图1,、为等边中边所在直线上两点,,求证:;(2)中,,请用不含刻度的直尺和圆规在上求作两点、,点在点的左侧,使得为等边三角形;
(3)在(1)的条件下,为边上一点,过作交延长线于点,交延长线于点,若,,,求的值.(用含有的代数式表示)
【答案】(1)见解析;(2)见解析;(3)
【分析】(1)根据等边三角形的性质可得,再由,可得,从而得到,即可;
(2)作,分别交于点B,C,即可;
(3)根据等边三角形的性质以及,可得,再由,可得,再由,可得,,可证得,从而得到,同理,可得,从而得到,即可求解.
【详解】(1)证明:∵是等边三角形,∴,
∴,∴,
∵,∴,
∴,∴;
(2)解:如图,即为所求;
理由:根据作图得:,
∴,∴,∴,
∵,∴,,
∵,,
∴,∴,∴是等边三角形;
(3)∵是等边三角形,∴,,
∵,,∴,
∴,∵,∴,
由(1)得:,∴,,
∴,即,∴,∴,
∴,同理,∴,∴,∴.
【点睛】本题主要考查了相似三角形的判定和性质,等边三角形的判定和性质,熟练掌握相似三角形的判定和性质,等边三角形的判定和性质是解题的关键.
例6.(2023·江西吉安·统考一模)综合与实践
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF,如图1.
(1)_________,写出图中两个等腰三角形:_________(不需要添加字母);
转一转:将图1中的绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2)线段BP、PQ、DQ之间的数量关系为_________;(3)连接正方形对角线BD,若图2中的的边AP、AQ分别交对角线BD于点M、点N.如图3,则________;
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.(4)求证:.
【答案】(1)45,,;(2);(3);(4)见解析
【分析】(1)由翻折的性质可知:,,根据正方形的性质:, ,则,为等腰三角形;
(2)如图:将顺时针旋转,证明全等,即可得出结论;
(3)证明即可得出结论;
(4)根据半角模型,将顺时针旋转,连接,可得,通过得出,为直角三角形,结合勾股定理即可得出结论.
【详解】(1)由翻折的性质可知:
为正方形,为等腰三角形
(2)如图:将顺时针旋转,
由旋转的性质可得:, 由(1)中结论可得
为正方形,
在和中
(3)为正方形对角线
,
,
(4)如图:将顺时针旋转,连接,
由(2)中的结论可证
根据旋转的性质可得:,
在中有
【点睛】本题是四边形的综合题,考查了正方形的性质,折叠的性质,旋转变换的性质,全等三角形的判定和性质,以及相似三角形的判定和性质,勾股定理等知识,能够综合运用这些性质是解题关键.
例7.(2023·湖北武汉·校考模拟预测)在矩形中, ,(),点E、F分别是边、上的点,过点F作,交直线于点G.
(1)如图1:若,,,,则________,________;
(2)如图2:若,,过点F作,交于点G,过E作,交于点H,求证:;(3)如图3:若,,过点F作,交于点G,,直接写出的值________.
【答案】(1),(2)见详解(3)
【分析】(1)由,可得四边形是正方形,将绕逆时针旋转,得到,可求,可证,设,由,即可求解;
(2)过作交的延长线于,取的中点,连接、,过作交于,可得,可证,可得,可证,可得,,设,可证,由,可证、、、四点共圆,可得,从而可得证;(3)过作交的延长线于,连接,由(2)得可证,,即可求解.
【详解】(1)解:
,四边形是正方形,,
,,,
如上图,将绕逆时针旋转,得到,
,,,
,、、三点共线,
,,,
在和中,(),,
设,则,,,,解得:,
,.故答案:,.
(2)证明:如图,过作交的延长线于,取的中点,连接、,过作交于,
,,,,,
四边形是矩形,,,
,,,
,,,,
,,,,
在和中,(),,,
,,设,则,
,
,,
,,,
,,,
、、、四点共圆,,
,,.
(3)解:如图,过作交的延长线于,连接,
由(2)得,同理可证,,
,,
在,.故答案:.
【点睛】本题考查了正方形的性质,矩形的性质,旋转的性质,三角形全等的判定及性质,三角形相似的判定及性质,中位线定理,等腰三角形的判定及性质,勾股定理等,掌握相关的判定方法及性质,并根据题意作出辅助线是解题的关键.
课后专项训练
1.(2022·成都市·八年级期末)如图,在边长为4的正方形ABCD中,对角线AC,BD交于点O,E在BD上,连接CE,作EF⊥CE交AB于点F,交AC于点G,连接CF交BD于点H,延长CE交AD于点M,连接FM,则下列结论:①点E到AB,BC的距离相等;②∠FCE = 45°;③∠DMC =∠FMC;④若DM = 2,则BF = .正确的有( )个.
A.1B.2C.3D.4
【答案】C
【分析】过E点作、,由正方形对角线平分每一组对角以及角平分线性质可得点E到AB,BC的距离相等,故①正确;再证明(AAS)可得是等腰直角三角形,得,故②正确;然后延长MD至P,使,(SAS)再证明(SAS)即可得,故③正确;由全等三角形性质和勾股定理列方程可求.
【详解】解:如图1,过E点作、,∴,
∵在正方形ABCD中,,,
∴,即点E到AB,BC的距离相等,故①正确;
;∴,由∵,∴,
∴,∴(AAS)∴,∴,故②正确;
如图2,延长MD至P,使,连接,易证(SAS)∴,,
∵,∴,∴,
又∵,∴,∴,∴,,故③正确,
在边长为4的正方形ABCD中,,若,则,
设,则,,
在中,∴,解得:,故;④错误,
综上所述,正确的①②③,故选C.
【点睛】本题主要考查了正方形和三角形综合知识,解题关键是构造全都三角形转换边角关系.
2.(2022·广东深圳·统考一模)如图,正方形ABCD中,E是BC的中点,F在CD上,,连接AE,AF与对角线BD交于点M,N,连接MF,EN.给出结论:①;②;③;④.其中正确的是( )
A.①②③B.①②④C.①③④D.②③④
【答案】A
【分析】将顺时针旋转,使得AB与AD重合,此时得,将逆时针旋转,使得AD与AB重合,此时得,根据,即可求得,①正确;根据可得,即可求,即可得③正确;根据如图正方形构造直角坐标系,求出直线AE、AF、BD的解析式,再联立解析式,即可求得M、N两点的坐标,再根据坐标求出DN、MN、BM、AN、NE,即可知,则有,则有,,②正确;根据DN、MN、BM长度可知,④错误.
【详解】将顺时针旋转,使得AB与AD重合,此时得,将逆时针旋转,使得AD与AB重合,此时得,链接EF,如图所示:
为了方便计算,设正方形的边长为6,则有AB=BC=CD=AD=6,
则有BE=EC=3=DG,CF=4,DF=2=BH,,则有:HE=5=FG,
利用勾股定理,易求得:AH=AF=,AE=AG=,EF=5,BD=,
根据图形的旋转,可知,,∴,
∵ AH=AF,HE=5=FG,AE=AE,∴,同理可证得,∴,
又∵,∴,故①正确;
∵,,∴,同理可证,
∴,∴,故③正确;
以B为坐标原点O,AB所在的直线为y轴,以BC所在的直线为x轴,构建直角坐标系,则有A点坐标为,B点坐标为,C点坐标为,D点坐标为,F点坐标为,E点坐标为,
则直线AF的解析式为:,BD的解析式为,AE的解析式为,
联立:,得到N点坐标为:,同理的M点坐标为,
过M点作MP垂直于BC,交BC于P点,过N点作NQ垂直于DC,交DC于Q点,
则有MP=2,,
则有,,
则有,
则有:,故④错误;
根据N点坐标为:,A点坐标为:,E点坐标为:,
可得,
则在中,,∴,∴,故②正确;故选:A.
【点睛】本题考查了直角坐标系的构建、相似三角形以及坐标系中求解两点间距离等知识.准确作出辅助线并构建直角坐标系是解答本题的关键.
3.如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( )
A.2B.C.D.3
【答案】A
【分析】构造如图所示的正方形,然后根据相似三角形的判定和性质解直角三角形FNP即可.
【详解】如图,延长CE,FG交于点N,过点N作,延长交于,
∴∠CMN=∠DPN=90°,∴四边形CMPD是矩形,
根据折叠,∠MCN=∠GCN,CD=CG,,
∵∠CMN=∠CGN=90°,CN=CN,∴,
∴,四边形为正方形,
∴,∴,
,,,设,则,
在中,由可得解得;故选A.
【点拨】本题考查了折叠问题,正方形的性质与判定,矩形的性质,平行线的性质,全等三角形的性质和判定,相似三角形,勾股定理等知识点的综合运用,难度较大.作出合适的辅助线是解题的关键.
4.(2022春·广东河源·八年级校考阶段练习)如图,在边长为6的正方形内作,交于点,交于点,连接,将绕点顺时针旋转90°得到,若,则的长为______.
【答案】5
【分析】由题意易得,则有,然后可证,则有,设,则有,进而根据勾股定理可求解.
【详解】解:∵四边形ABCD是正方形,且边长为6,
∴,∵绕点顺时针旋转90°得到,
∴,∴点G、B、E三点共线,
∵,∴,∵AE=AE,∴,∴,
设,则有,∴在Rt△ECF中,由勾股定理可得,
即,解得:,∴;故答案为5.
【点睛】本题主要考查正方形的性质、旋转的性质及勾股定理,熟练掌握正方形的性质、旋转的性质及勾股定理是解题的关键.
5.(2023·浙江绍兴·校联考三模)矩形中,,,连接,E,F分别在边,上,连接,分别交于点M,N,若,,则的长为 .
【答案】
【分析】根据矩形的性质,由勾股定理得出,延长至P,使,过P作的平行线交的延长线于Q,得正方形,延长交于H,连接,将绕点A顺时针旋转,点D与点P重合,得到,由旋转的性质可得,,,,证出,得出,可证,得出,证出,设,则,利用勾股定理列出方程求出,然后由,得,所以 ,即可求出的长.
【详解】解:在矩形中, ∵,,,
∴,
如图,延长至P,使,过P作的平行线交的延长线于Q,得正方形, 延长交于H,连接, 将绕点A顺时针旋转,点D与点P重合,得到,
∵四边形是正方形,
∴,,
由旋转得:,
∴,,,,
∴, 即, ,,三点共线,
∵, ∴, ∴,
在和中,, ∴, ∴,
∵, ∴, 设,则,
∵,,∴, ∴, ∴,
∴,, 在中,由勾股定理得:,
∴(, 解得:, ∴,
∵, ∴, ∴ ,
∴. 故答案为:.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等知识;证明三角形全等和由勾股定理得出方程是解题的关键.
6.(2023·成都市·九年级专题练习)如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2;⑤BE=EF﹣DC;其中正确的选项是 (填序号)
【答案】①③④
【分析】①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②当△ABE∽△ACD时,该比例式成立;
③根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;
④据①知BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF;由此即可确定该说法是否正确.
【详解】解:①根据旋转的性质知∠CAD=∠BAF,AD=AF.
∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°,
∴∠EAF=45°,∴△AED≌△AEF;故本选项正确;
②∵AB=AC,∴∠ABE=∠ACD;∴当∠BAE=∠CAD时,△ABE∽△ACD,
∴;当∠BAE≠∠CAD时,△ABE与△ACD不相似,即;
∴此比例式不一定成立,故本选项错误;③根据旋转的性质知△ADC≌△AFB,
∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积,故本选项正确;
④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2.
∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD.
又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;
⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,
∴BE+DC=BE+BF>DE=EF,即BE+DC>FE,故本选项错误.
综上所述:正确的说法是①③④.故答案为:①③④.
【点睛】本题考查了图形的旋转变换以及全等三角形的判定等知识,三角形三边的关系,相似三角形的性质与判定,解题时注意旋转前后对应的相等关系.
7.(2023·上海宝山·校考一模)如图,在△ABC中,AB=AC ,点D、E在边BC上,∠DAE=∠B=30°,且,那么的值是 .
【答案】.
【分析】由已知可得,从而可知,,
设AB=3x,则BE=2x,再利用勾股定理和等腰三角形性质用x表示DE和BC,从而解答
【详解】解:∵∠BAE=∠DAE+∠BAD,∠ADE=∠B+∠BAD,
又∵∠DAE=∠B=30°,∴∠BAE=∠ADE,∴,∴,,
过A点作AH⊥BC,垂足为H,
设AB=3x,则BE=2x,
∵∠B=30°,∴,,∴,
在中,,
又∵,∴,∴,
∵AB=AC,AH⊥BC,∴,∴,
故答案为: .
【点睛】本题考查了相似三角形的判定和性质、等腰三角形的性质以及勾股定理,利用三角形相似得到AB与BE的关系是解题的关键.
8.(2022·江苏南京·九年级专题练习)(1)阅读理解:如图1,在正方形ABCD中,若E,F分别是CD,BC边上的点,∠EAF=45°,则我们常会想到:把△ADE绕点A顺时针旋转90°得到△ABG.易证△AEF≌_______,得出线段BF,DE,EF之间的数量关系为____________;
(2)类比探究:如图2,在等边△ABC中,D,E为BC边上的点,∠DAE=30°,BD=3,EC=4,求线段DE的长;(3)拓展应用:如图3,在△ABC中,AB=AC,∠BAC=150°,点D,E在BC边上,∠DAE=75°,若DE是等腰△ADE的腰长,请直接写出BD:CE的值.
【答案】(1);;(2);(3)或
【分析】(1)由旋转的性质可得,,,进而得到,由全等三角形的性质可得,即可解答;(2)将绕点顺时针旋转,得到,连接,过点作,交的延长线于点,进而证≌,得到,即可求出和,再根据勾股定理即可解答;(3)用的方法,分类讨论是等腰的腰长,求出:的值即可.
【详解】解:(1)把绕点顺时针旋转得到,可知:,,,
,,
在和中,≌,,
,,故答案为;.
(2)如图,将△ACE绕点A顺时针旋转60°,得到△ABF,连接DF,过点F作FG⊥BC,交CB的延长线于点G,如图所示:
∵△ABC是等边三角形,∴∠CAB=∠ABC=∠C=60°,AB=AC,
∵∠DAE=30°,∴∠CAE+∠BAD=30°,∴∠DAF=30°,
又∵AD=AD,∴△ADE≌△ADF,∴DE=DF,∵∠ABF=∠ABC=∠C=60°,∠FBG=60°,
∵BF=CE=4,∠G=90°,∴BG=BF=2,FG==,
∴DG=5,∴在Rt△DFG中,DF=,∴线段DF的长为.
(3)如图,将△ACE绕点A顺时针旋转150°,得到△ABG,连接DG,过点D作DH⊥BG,交BG的于点H,∠DAE=75°,若DE是等腰△ADE的腰,∠ADE为顶角,则∠ADE=30°,
∵AB=AC,∠BAC=150°,∴∠ABC=∠C=(180°-150°)=15°,
∴由旋转性质得△ABG≌△ACE,∴BG=CE,AG=AE,∠ABG=∠C=15°,∴∠DBG=30°,
∵将△ACE绕点A顺时针旋转150°,得到△ABG,∴∠EAG=150°,
∵∠DAE=75°,∴∠GAD=75°,∴∠ADE=30°,
在△ADE和△ADG中,,∴△ADE≌△ADG,∴∠GDA=∠ADE=30°,∴∠GDE=60°,
∵∠GDE=∠GBD+∠BGD,∴∠BGD=60°-30°=30°,∴BD=DG,∴BH=GH=BG=CE,
在Rt△BHD中,设HD=x,∵∠DBG=30°,∴BD=2x,由勾股定理得:BH=,
∴BG=2,∴CE=2,∴BD:CE=:3;
如图将△ACE绕点A顺时针旋转150°,得到△ABM,连接DM,过点M作MN⊥BD,交BD于点N,
∵∠DAE=75°,若DE是等腰△ADE的腰长,∠E为顶角,∴∠E=30°,
∵AB=AC,∠BAC=150°,∴∠C=∠ABC=15°,∴∠CAE=15°,
∴AE=CE=DE,∴∠BAD=150°-75°-15°=60°,由旋转性质可知△ABM≌△ACE,
∴∠BAM=∠CAE=15°,∠ABM=∠ACE=15°,AM=AE,BM=CE,∴∠MAD=15°+60°=75°=∠DAE,
在△MAD和△EAD中,,∴△MAD≌△EAD,∴DM=DE=CE=BM,
∵MN⊥BD,∴BN=DN=BD,∵∠MBD=∠ABM+∠ABC=15°+15°=30°,
∴在Rt△BNM中 ,设MN=a,∴BM=2a,∴CE=2a,
由勾股定理得:BN=,∴BD=2a,∴BD:CE=2a:2a=:1=.
【点睛】本题考查了四边形的综合题,正方形的性质,全等三角形的判定和性质,旋转的性质,正确的作出辅助线是解题的关键.
9.(2022·湖北十堰·中考真题)【阅读材料】如图①,四边形中,,,点,分别在,上,若,则.
【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知,,,,道路,上分别有景点,,且,,若在,之间修一条直路,则路线的长比路线的长少_________(结果取整数,参考数据:).
【答案】370
【分析】延长交于点,根据已知条件求得,进而根据含30度角的直角三角形的性质,求得,,从而求得的长,根据材料可得,即可求解.
【详解】解:如图,延长交于点,连接,
,,,,,
是等边三角形,,,
在中,,,
,,,
中,,,
,
,
,中,
是等腰直角三角形
由阅读材料可得,
路线的长比路线的长少.答案:370.
【点睛】本题考查了含30度角的直角三角形的性质,勾股定理,理解题意是解题的关键.
10.(2022·山东青岛九年级期中)【模型引入】
当几何图形中,两个共顶点的角所在角度是公共大角一半的关系,我们称之为“半角模型”
【模型探究】(1)如图1,在正方形ABCD中,E、F分别是AB、BC边上的点,且∠EDF=45°,探究图中线段EF,AE,FC之间的数量关系.
【模型应用】(2)如图2,如果四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45°,且BC=7,DC=13,CF=5,求BE的长.
【拓展提高】(3)如图3,在四边形ABCD中,AB=AD,∠ABC与∠ADC互补,点E、F分别在射线CB、DC上,且∠EAF∠BAD.当BC=4,DC=7,CF=1时,CEF的周长等于 .
(4)如图4,正方形ABCD中,AMN的顶点M、N分别在BC、CD边上,AH⊥MN,且AH=AB,连接BD分别交AM、AN于点E、F,若MH=2,NH=3,DF=2,求EF的长.
(5)如图5,已知菱形ABCD中,∠B=60°,点E、F分别是边BC,CD上的动点(不与端点重合),且∠EAF=60°.连接BD分别与边AE、AF交于M、N,当∠DAF=15°时,求证:MN2+DN2=BM2.
【答案】(1)EF=FC+AE,理由见解析;(2)BE=5;(3)13;(4)EF=;(5)见解析
【分析】(1)求证△DEF≌△DMF,即可推出EF与FM的数量关系;
(2)在DC上取一点G,使得DG=BE,证明△ABE≌△ADG(SAS),推出AE=AG,∠BAE=∠DAG,证明△AFE≌△AFG(SAS),推出EF=FG,设BE=x,则CG=13-x,EF=FG=18-x,在Rt△ECF中,根据EF2=EC2+CF2,构建方程求出x即可解决问题;
(3)证明△ADM≌△ABE(SAS)和△EAF≌△MAF,即可求解;
(4)先求出BM,DN,进而求出正方形的边长,再判断出∠EAF=45°,借助探究的结论即可得出结论.
(5)将△ADF绕A顺时针旋转120°,AD与AB重合,F转到G,在AG上取AH=AN,连接BH、MH,利用△ABH≌△ADN和△AMH≌△AMN,证明MN=MH,DN=BH,再证明△BMH为直角三角形即可.
【详解】(1)EF=FC+AE,理由如下:
证明:将△DAE绕点D逆时针旋转90°,得到△DCM,∴△DAE≌△DCM,
∴DE=DM,AE=CM,∠ADE=∠CDM,B、C、M三点共线,
∵∠EDF=45°,∴∠ADE+∠FDC=∠CDM+∠FDC=∠MDF=45°,
在△DEF和△DMF中,
,∴△DEF≌△DMF(SAS),∴EF=FM
∴EF=FM=FC+CM=FC+AE;
(2)解:如图,在DC上取一点G,使得DG=BE,
∵∠BAD=∠BCD=90°,∴∠ABC+∠D=180°,∠ABE+∠ABC=180°,∴∠ABE=∠D,
∵AB=AD,BE=DG,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,
∵∠EAF=45°,∴∠EAB+∠BAF=∠DAG+∠BAF=45°,
∵∠BAD=90°,∴∠FAG=∠FAE=45°,
∵AE=AG,AF=AF,∴△AFE≌△AFG(SAS),∴EF=FG,
设BE=x,则EC=EB+BC=x+7,EF=FG=18-x,
在Rt△ECF中,∵EF2=EC2+CF2,
∴52+(7+x)2=(18-x)2,∴x=5,∴BE=5;
(3)解:在DF上截取DM=BE,
∵∠D+∠ABC=∠ABE+∠ABC=180°,∴∠D=∠ABE,
∵AD=AB,∴△ADM≌△ABE(SAS),∴AM=AE,∠DAM=∠BAE;
∵∠EAF=∠BAE+∠BAF=∠BAD,∴∠MAF=∠BAD,∴∠EAF=∠MAF;
∵AF是△EAF与△MAF的公共边,∴△EAF≌△MAF,∴EF=MF;
∵MF=DF-DM=DF-BE,∴EF=DF-BE.
∴△CEF的周长=CE+EF+FC=BC+BE+DC+CF-BE+CF=BC+CD+2CF=13,故答案为:13;
(4)解:∵四边形ABCD是正方形,∴AB=AD,∠ABC=∠ADC=90°,
∵AH⊥MN,∴∠AHM=∠ABC=90°,在Rt△AMB和Rt△AMH中,
,∴Rt△AMB≌Rt△AMH,∴∠MAB=∠MAH,BM=MH=2,
同理可证Rt△AND≌Rt△ANH,∴∠NAD=∠NAH,DN=NH=3,
∴2∠MAH+2∠NAH=90°,∴∠MAH+∠NAH=45°,
∴∠MAN=45°.设正方形的边长为a,∴CM=a-2,CN=a-3,
根据勾股定理得,(a-2)2+(a-3)2=25,∴a=-1(舍)或a=6,∴BC=6,∴BD=6,
逆时针旋转△ABE至△ADG,
∴△ABE≌△ADG,∴AE=AG,∠ABE=∠ADG=45°,
∴∠GDF=∠ADG+∠ADB=90°,连接GF,根据勾股定理得,GF2=DG2+DF2=BE2+DF2,
∵△ABE≌△ADG,∴AE=AG,∠BAE=∠DAG,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=90°-∠EAF=45°=∠EAF,
∵AF=AF,∴△GAF≌△EAF,∴GF=EF,∴EF2=BE2+AD2;
设EF=x,∵BD=6,DF=2.∴BE=6-2-x=4-x,
∴(4-x)2+(2)2=x2,解得x=,∴EF=;
(3)将△ADF绕A顺时针旋转120°,此时AD与AB重合,F转到G,在AG上取AH=AN,连接BH、MH,如图:∵△ADF绕A顺时针旋转得△ABG,∴∠BAG=∠DAF,
又AH=AN,AB=AD,∴△ABH≌△ADN(SAS),∴DN=BH,∠ABH=∠ADN,
∵∠B=60°,且∠EAF=60°.∴∠BAD=120°,∴∠DAF+∠BAE=∠EAF=60°,
∴∠BAG+∠BAE=∠EAF,即∠MAH=∠MAN,而AH=AN,AM=AM,
∴△AMH≌△AMN(SAS),∴MN=MH,∠AMN=∠AMH,
∵菱形ABCD,∠B=60°,∴∠ABD=∠ADB=30°,∴∠HBD=∠ABH+∠ABD=60°,
∵∠DAF=15°,∠EAF=60°,∴△ADM中,∠DAM=∠AMD=75°,∴∠AMN=∠AMH=75°,
∴∠HMB=180°-∠AMN-∠AMH=30°,∴∠BHM=90°,∴BH2+MH2=BM2,∴DN2+MN2=BM2.
【点睛】本题是四边形综合题,主要考查了旋转的性质、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题关键是学会用旋转法添加辅助线,构造全等三角形解决问题,学会利用探究的结论解决新的问题,属于中考压轴题.
11.(2022·江西九江·一模)如图(1),在四边形ABCD中,,,以点A为顶点作,且,连接EF.(1)观察猜想 如图(2),当时,
①四边形ABCD是______(填特殊四边形的名称);②BE,DF,EF之间的数量关系为______.(2)类比探究 如图(1),线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请加以证明;若不成立,请说明理由.(3)解决问题 如图(3),在中,,,点D,E均在边BC上,且,若,求DE的长.
【答案】(1)①正方形;②BE+ DF=EF(2)详见解析(3)详见解析
【分析】(1)①根据正方形的判定定理即可得出;
②延长CD至点G,使得DG=BE,证得,得出,由,证得,从而得出BE,DF,EF之间的数量关系;(2)同(1)②即可得出BE,DF,EF之间的数量关系;(3)作,且,证得,同(1)②证得,在中,由勾股定理可解得DE的长.
(1)解:①∵,∴四边形ABCD是矩形,又∵,∴矩形ABCD是正方形.
②如下图,延长CD至点G,使得DG=BE,
∵,,∴,∴,
∴,,,∵,∴,
∴,即,
又∵,∴,∴,即∴.
(2)如下图,延长CD至点H,使得DH=BE,∵,∴,
同(1)②的证明方法得,同理证,从而得.
(3)如图过点C作,且,
在中, 由, ,
∴,∴,∴,
同(1)②的证明方法得,∴,
∵,,,,
设,则,
在中,由勾股定理得,,,解得,即.
【点睛】本题考查了特殊的平行四边形的判定、全等三角形的性质和判定及勾股定理的应用,熟练应用相关定理和性质是解决本题的关键.
12.(2023·福建泉州·统考二模)(1)如图1,在正方形中,,分别为,边上的点,且满足,连接,则,,之间的数量关系为________.
(2)如图2,将沿斜边翻折得到,,分别为,边上的点,且,试猜想,,之间的数量关系,并证明你的猜想.
(3)将两个全等的等腰直角和按如图3所示摆放在一起,为公共顶点,,,与边的交点分别为,,求证:.
【答案】(1);(2),证明见解析;(3)证明见解析
【分析】(1) 将绕点顺时针旋转到的位置,证出,进而证出,得出结论;(2) 将绕点顺时针旋转到的位置,证出,进而证出,得出结论;(3) 将绕点顺时针旋转至的位置,证出,由勾股定理得出结论.
【详解】解:(1). 理由如下:
如图,将绕点顺时针旋转到的位置,
由旋转可得,.,.
在和中,,∴,∴.
∵,∴.
(2),理由如下: 如图,将绕点顺时针旋转到的位置,
由旋转可得,,.
∵,∴,,三点共线.
∵,∴,∴.
在和中,,∴,∴.
∵,∴.
(3)证明:如图,将绕点顺时针旋转至的位置,
则,,,旋转角.连接,在和中,
∵,,.∴,∴.
∵,∴,∴.
【点睛】本题考查旋转的性质,全等三角形的判定和性质,勾股定理.其中准确作出辅助图形是解题关键.
13.(2023·陕西西安·九年级校考期中)问题研究,如图,在等腰中,,点、为底边上的两个动点(不与、重合),且.
(1)请在图中找出一个与相似的三角形,这个三角形是__________;
(2)若,分别过点、作、的垂线,垂足分别为、,且、的反向延长线交于点,若,求四边形的面积;
问题解决(3)如图所示,有一个矩形仓库,其中米,米,现计划在仓库的内部的、两处分别安装监控摄像头,其中点在边上,点在边上.设计要求且,则的长应为多少米?
【答案】(1);(2)四边形的面积为;(3)CE的长为米.
【分析】(1)根据已知条件及相似三角形的判定可直接得出;
(2)把绕点A逆时针旋转得到,连接EH,根据旋转可得,利用三角形全等的性质得出,,,利用角和边之间的关系可得:为直角三角形,根据勾股定理及等量代换得出,根据全等三角形的判定得出≅,得,再求出各三角形的面积确定,再根据图形中三角形的关系得出,即可求得四边形面积;
(3)根据(2)中思路,作图:延长AD到S,延长BC到G,使,连接SG,延长AF交SG于点H,连接EH,延长GS到T,使,连接AT,则四边形ABGS为正方形,根据全等三角形的判定定理得出≅,根据全等三角形的性质及等量代换得出,再利用三角形全等的判定证明≅,设,可得出,,,在根据相似三角形的判定和性质得出,将各边代入得出,,,在中,利用勾股定理得出方程求解即可.
【详解】解:(1)∵,,
∴,故答案为:;
(2)如图所示:把绕点A逆时针旋转得到,连接EH,
∴,,∴,,,
∵,,∴,
∴,∴,
∴,∴,
∵,∴,∵,∴,
在和中,,∴≅,∴,∴,
∵于点G,,∴,
∴,∴,∵,∴,同理可得:,
在中,,∴,同理可得:,
∵,∴,∴,即,
∵,∴,即四边形的面积为;
(3)如图,延长AD到S,延长BC到G,使,连接SG,延长AF交SG于点H,连接EH,延长GS到T,使,连接AT,则四边形ABGS为正方形,
∴,,
在和中,,∴,,
∴,,∴,
在和中,,∴≅,∴,
设,则,,,
∵DFSH,∴,∴,即:,
解得:,∴=,
,
∴在中,,
解得:,(舍去),即CE的长为米.
【点睛】题目主要考查相似三角形的判定和性质、全等三角形的判定和性质、勾股定理、一元二次方程的运用求解等,根据题意作出相应辅助线,融会贯通综合运用这些知识点是解题关键.
14.(2023·陕西汉中·九年级统考期末)如图,中,,,点为边上一点.
(1)如图1,若,.①求证:;②若,求的值.
(2)如图2,点为线段上一点,且,,,求的长.
【答案】(1)①见解析,②(2)
【分析】(1)①通过证明,即可求证;②由①可得,再根据等边对等角求出和的度数,即可得出,最后根据直角三角形中角所对的边是斜边的一半即可求证;
(2)过点E作于G,过A作于F,证明,可以求出,利用勾股定理可以求出的长,从而可以求解.
【详解】(1)证明:①∵,,
∴,即,
在和中,,∴,∴;
②∵,,∴,
由①可得:,∴,
∴,
∵,∴在中,,
∴,整理得:,由①可得,∴.
(2)过点A作于点F,过点E作于点G,
∵,,∴,
∵,,∴,
在中,根据勾股定理可得:,
∵,∴,
∵,,∴,
在中,根据勾股定理可得:,
∴,
∵,,,∴,
∵,∴,即,
∵,∴,
∴,即,解得:,∴.
【点睛】本题主要考查了全等三角形的性质与判定,等腰三角形的性质,含30度角的直角三角形的性质,勾股定理等等,解题的关键在于能够熟练掌握相关知识进行求解.
15.(2023·辽宁沈阳·九年级统考期末)【教材呈现】
(1)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠G=90°,BC=6,若△ABC固定不动,将△AFG绕点A旋转,边AF、AG与边BC分别交于点D,E(点D不与点B重合,点E不与点C重合)①求证:AE2=DE•BE;②求BE•CD的值;
【拓展探究】(2)如图2,在△ABC中,∠C=90°,点D,E在边BC上,∠B=∠DAE=30°,且,请直接写出的值.
【答案】(1)①证明见解析;②18;(2)
【分析】(1)①只需要证明△ABE∽△DAE,得到,即可推出;
②先证明∠AEB=∠DAC,则可证△AEB∽△DAC,推出,然后利用勾股定理求出,即可得到;
(2)设,,先证明△ADE∽△BDA,推出,设,,得到,求出,,则在直角△ACD中,,则,即可推出,由此求解即可.
【详解】解:(1)①∵△ABC和△AGF都是等腰直角三角形,∠BAC=∠G=90°,∴∠B=∠C=∠GAF=45°,
又∵∠AED=∠NEA,∴△ABE∽△DAE,∴,∴;
②∵∠DAC=∠DAE+∠CAE,∠AEB=∠C+∠CAE,∠C=∠DAE=45°,∴∠AEB=∠DAC,
又∵∠B=∠C,∴△AEB∽△DAC,∴,∴,
∵AB=AC,∠BAC=90°,BC=6,∴,即,
∴,∴;
(2)∵,∴可设,,
∵∠B=∠DAE=30°,∠ADE=∠BDA,∴△ADE∽△BDA,
∴,∴,可设,,∴,
∵∠B=30°,∠ACB=90°,∴,∴,
∴ 在直角△ACD中,,
∴,∴,∴.
【点睛】本题主要考查了等腰直角三角形的性质,相似三角形的性质与判定,含30度角的直角三角形的性质,勾股定理等等,熟练掌握相似三角形的性质与判定条件是解题的关键.
16.(2022秋·广东·九年级校考期中)如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.
【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.
(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.
(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.
【答案】(1)12(2)猜想:,理由见解析(3)4
【分析】(1)由旋转的性质可得△ABE≌△ADM, 易证:△ANM≌△ANE,从而得DM+BN=MN.则可得MN+CM+CN=2BC,从而可求得正方形的边长;
(2)过点D作DP⊥DF,且DP=BE,连接PF、AP,可证明△APD≌△AEB,则可得AP=AE,∠EAP=90°;再证明△APF≌△AEF,可得EF=FP,在Rt△PDF中,由勾股定理即可得三条线段EF、BE、DF之间满足的数量关系; (3)把矩形ABCD补成正方形AEFD,延长AN交EF于G,连接GN.由△ABN∽△AEG,可求得EG、FG的长,设DM=x,则可得FM,由(1)的证明知,GM=EG+DM,由勾股定理建立方程即可求得x的值,即DM的长.
【详解】(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ABC=∠C=∠D=90°.由旋转得:△ABE≌△ADM,
∴AE=AM,BE=DM,∠ABE=∠D=90°,∠EAB=∠MAD.
∴∠ABE+∠ABC=180°.∴E、B、N在同一直线上.∵∠MAN=45°,∠BAD=90°,∴∠BAN+∠MAD=45°.
∴∠BAN+∠EAB=45°.即∠EAN=45°.∴∠EAN=∠MAN.
在△ANM与△ANE中,∴△ANM≌△ANE.∴MN=EN.
∵EN=BE+BN=DM+BN, ∴MN=DM+BN.∴MN+CM+CN=DM+BN+CM+CN=CD+BC=2BC.
在Rt△CMN中,由勾股定理得:,
∴10+8+6=2BC.∴BC=12.故答案为:12.
(2)三条线段EF、BE、DF之间满足的数量关系为;
理由如下:如图②,过点D作DP⊥DF,且DP=BE,连接PF、AP.
则∠PDA+∠ADF=∠ADF+∠NDM=90°.∴∠PDA=∠NDM.∵四边形ABCD是正方形,∴BN∥DM.
∵BN=DM,∴四边形BNDM是平行四边形.∴∠EBA=∠NDM.∴∠PDA=∠EBA.
在△APD与△AEB中, ∴△APD≌△AEB.∴AP=AE,∠PAD=∠EAB.
∵∠EAP=∠EAD+∠PAD=∠EAD+∠EAB=∠BAD=90°,∠EAF=45°,∴∠PAF=∠EAF=45°.
在△APF与△AEF中,∴△APF≌△AEF.∴EF=FP.
在Rt△PDF中,由勾股定理得:,即.
(3)如图③,把矩形ABCD补成正方形AEFD,延长AN交EF于G,连接GN,则AE=EF=DF=AD=8.
∵四边形ABCD是矩形,∴BN∥EG.∴△ABN∽△AEG.
∴.∴.∴.
设DM=x,则FM=DF−DM=8−x,∵四边形AEFD是正方形,∠GAM=45°,
∴由(1)的证明知,.在Rt△GMF中,勾股定理得:,
即,解得:x=4即DM的长为4.
【点睛】本题是四边形的综合问题,考查了正方形性质,平行四边形的判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,旋转的性质等知识,综合性较强,证明三角形全等及由勾股定理得出方程是关键.
17.(2023·浙江杭州·九年级期中)已知正方形的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边、的延长线交于点E、F,连接.设.
(1)如图1,当被对角线平分时,求a、b的值;(2)当是直角三角形时,求a、b的值;(3)如图3,探索绕点A旋转的过程中,的面积是否发生变化?请说明理由.
【答案】(1);(2)当时,,;当时,,;(3)的面积不变,证明见解析
【分析】(1)利用正方形的性质可得,由被对角线平分可得,从而可证≌,根据全等三角形的性质可得,然后根据角度关系可得,即可得到a、b的值;(2)由题意可知,分两种情况计算,①当时,首先根据题意得到是等腰直角三角形,再根据勾股定理得到,根据已知条件可得∽,根据相似三角形的性质得出,两式联立解方程组即可;②当时,方法和上面的方法一致,即可解答;(3)先利用平行线的性质和正方形的性质得到,再利用三角形的内角和得到,从而求出,而,得到∽,然后再利用相似三角形的对应边成比例,即可求出的值,进而可知的面积是否变化.
【详解】(1)∵四边形是正方形,∴,
∵是正方形的对角线,∴,∴,
∵被对角线平分,∴,
在和中,,∴≌,
∴,,∵,,∴,
∵,∴,∵,,∴,
∵,∴,∴,即;
(2)当是直角三角形时,①当时,∵,∴,
∴是等腰直角三角形,∴,
∵,∴,∴,
∴,∴,∴①
∵,,∴,∴∽,
∴,∴,∴②,
联立①②得,,,∴,;
②当时,同①的方法得,,,∴,;
(3)∵,∴,∵,∴,∴,
∵,∴,
∵,∴∽∴,
∴,∴,
∵,∴,∴的面积不变.
【点睛】此题是四边形的综合题,本题考查了全等三角形的判定和性质,直角三角形的性质,相似三角形的性质和判定,解本题的关键是判断∽,也是本题的难点.
18.(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形.如图①,把一个含有角的三角尺放在正方形中,使角的顶点始终与正方形的顶点重合,绕点旋转三角尺时,角的两边,始终与正方形的边,所在直线分别相交于点,,连接,可得.
【探究一】如图②,把绕点C逆时针旋转得到,同时得到点在直线上.求证:;【探究二】在图②中,连接,分别交,于点,.求证:;
【探究三】把三角尺旋转到如图③所示位置,直线与三角尺角两边,分别交于点,.连接交于点,求的值.
【答案】[探究一]见解析;[探究二]见解析;[探究三]
【分析】[探究一]证明,即可得证;[探究二]根据正方形的性质证明,根据三角形内角和得出,加上公共角,进而即可证明。[探究三]先证明,得出,,将绕点顺时针旋转得到,则点在直线上.得出,根据全等三角形的性质得出,进而可得,证明,根据相似三角形的性质得出,即可得出结论.
【详解】[探究一] ∵把绕点C逆时针旋转得到,同时得到点在直线上,
∴,∴,∴,
在与中∴∴
[探究二]证明:如图所示,
∵四边形是正方形,∴,
又,∴,∵,∴,
又∵,∴,
又∵公共角,∴;
[探究三] 证明:∵是正方形的对角线,
∴,,∴,
∵,∴,
即,∴,∴,,
如图所示,将绕点顺时针旋转得到,则点在直线上.
∴,,∴,
又,∴,∴,
∵,∴,又,∴,
∴,即.
【点睛】本题考查了全等三角形的性质与判定,旋转的性质,正方形的性质,相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
专题40 重要的几何模型之模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用): 这是一份专题40 重要的几何模型之模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用),文件包含专题40重要的几何模型之模型原卷版docx、专题40重要的几何模型之模型解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
专题18 全等与相似模型之十字模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用): 这是一份专题18 全等与相似模型之十字模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用),文件包含专题18全等与相似模型之十字模型原卷版docx、专题18全等与相似模型之十字模型解析版docx等2份试卷配套教学资源,其中试卷共77页, 欢迎下载使用。
专题15 全等与相似模型-手拉手模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用): 这是一份专题15 全等与相似模型-手拉手模型-备战2024年中考数学常见模型题型归纳与总结高分突破(全国通用),文件包含专题15全等与相似模型-手拉手模型原卷版docx、专题15全等与相似模型-手拉手模型解析版docx等2份试卷配套教学资源,其中试卷共78页, 欢迎下载使用。












