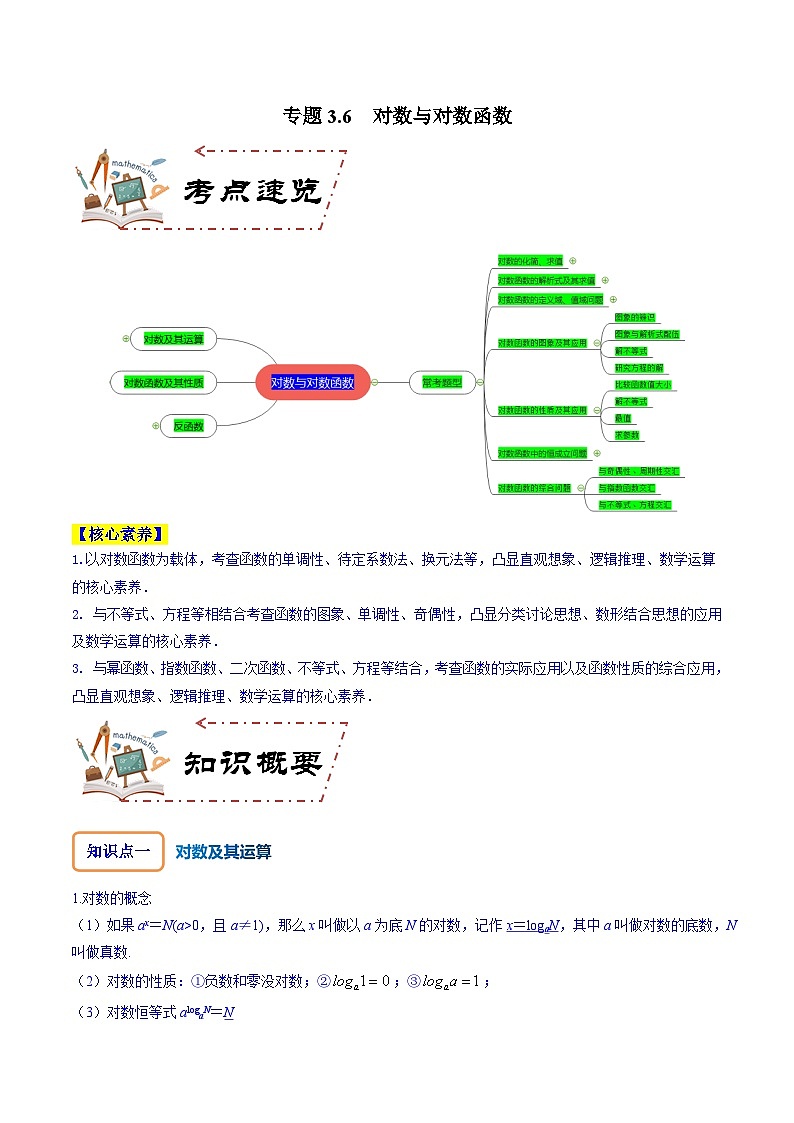
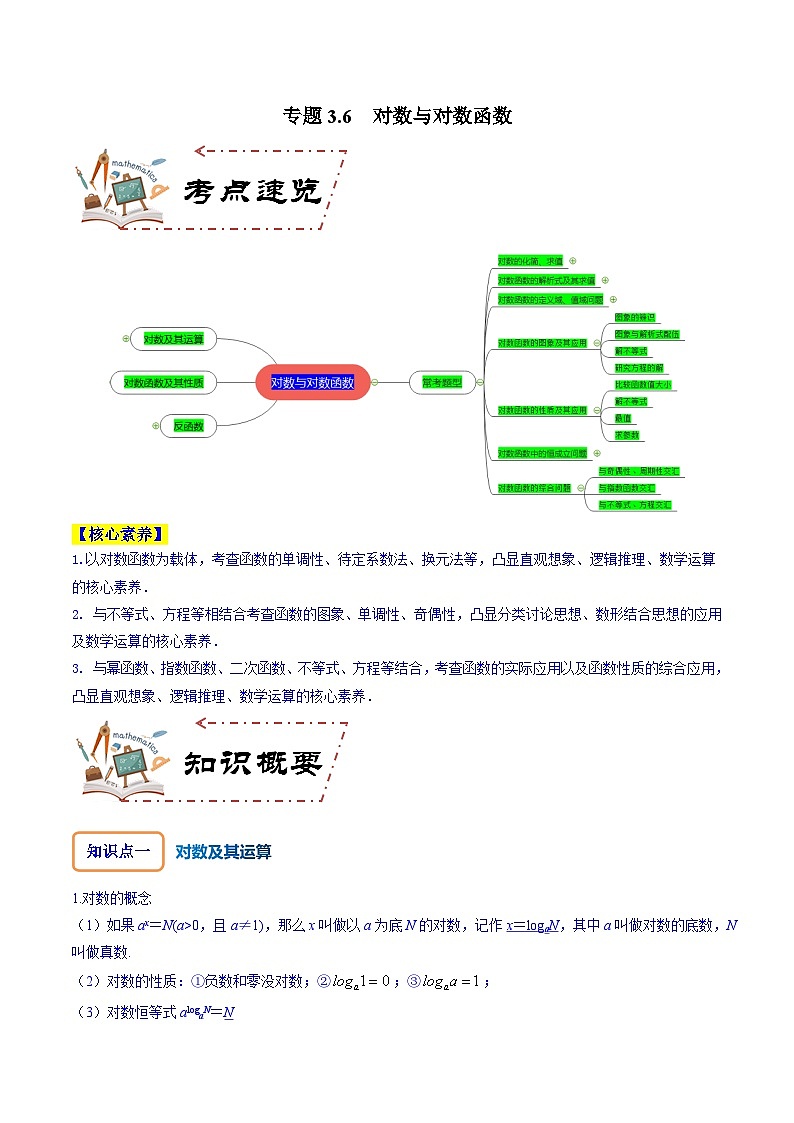
专题3.6 对数与对数函数-2024年高考数学大一轮复习核心考点精讲精练（新高考专用）

这是一份专题3.6 对数与对数函数-2024年高考数学大一轮复习核心考点精讲精练（新高考专用），文件包含专题36对数与对数函数原卷版docx、专题36对数与对数函数解析版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。


【核心素养】
1.以对数函数为载体，考查函数的单调性、待定系数法、换元法等，凸显直观想象、逻辑推理、数学运算的核心素养．
2. 与不等式、方程等相结合考查函数的图象、单调性、奇偶性，凸显分类讨论思想、数形结合思想的应用及数学运算的核心素养．
3. 与幂函数、指数函数、二次函数、不等式、方程等结合，考查函数的实际应用以及函数性质的综合应用，凸显直观想象、逻辑推理、数学运算的核心素养．
知识点一
对数及其运算
1.对数的概念
（1）如果ax＝N(a>0，且a≠1)，那么x叫做以a为底N的对数，记作x＝lgaN，其中a叫做对数的底数，N叫做真数.
（2）对数的性质：①负数和零没对数；②； = 3 \* GB3 ③；
（3）对数恒等式algaN＝N
2.对数的运算法则
如果a>0且a≠1，M>0，N>0，那么
①lga(MN)＝lgaM＋lgaN；
②lgaeq \f(M,N)＝lgaM－lgaN；
③lgaMn＝nlgaM(n∈R)；
④lgamMn＝eq \f(n,m)lgaM(m，n∈R，且m≠0).
(3)对数的重要公式
①换底公式：lgbN＝eq \f(lgaN,lgab)(a，b均大于零且不等于1)；
②lgab＝eq \f(1,lgba)，推广lgab·lgbc·lgcd＝lgad.
= 3 \* GB3 ③lgaab＝b(a>0，且a≠1)
知识点二
对数函数及其性质
1.概念：函数y＝lgax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞).
2.对数函数的图象与性质
3.对数函数的图象规律
(1)不管a>1还是0(2)在第一象限内，依图象的分布，逆时针方向a逐渐变小，即a的值越小，图象越靠近y轴．
知识点三
反函数
对数函数y＝lgax(a＞0，且a≠1)和指数函数y＝ax(a＞0，且a≠1)互为反函数，它们的图象关于直线y＝x对称．
常考题型剖析
题型一：对数的化简、求值
【典例分析】
例1-1. （2022·浙江·统考高考真题）已知，则（ ）
A．25B．5C．D．
例1-2. （2022·天津·统考高考真题）化简的值为（ ）
A．1B．2C．4D．6
例1-3. （2020·全国高考真题（理））已知55<84，134<85．设a=lg53，b=lg85，c=lg138，则（ ）
A．a【规律方法】
1.对数性质在计算中的应用
(1)对数运算时的常用性质：lgaa＝1，lga1＝0.
(2)使用对数的性质时，有时需要将底数或真数进行变形后才能运用；对于多重对数符号的，可以先把内层视为整体，逐层使用对数的性质．
2.对数运算的一般思路
(1)拆：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后利用对数运算性质化简合并．
(2)合：将对数式化为同底数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．
【变式训练】
变式1-1. （2020·全国·统考高考真题）设，则（ ）
A．B．C．D．
变式1-2. （2023·全国·高三专题练习）若，则的值为（ ）
A．B．3C．4D．
变式1-3. （2023·天津武清·天津市武清区杨村第一中学校考模拟预测）已知，，且，则的最小值为（ ）
A．B．21C．25D．
题型二：对数函数的解析式及其求值
例2-1. （2023·广东东莞·统考模拟预测）已知函数，则（ ）
A．4B．5C．6D．7
例2-2.（2023·全国·高三专题练习）写出一个具有性质①②③的函数____________.
①的定义域为；
②；
③当时，.
例2-3.（2023·北京·统考高考真题）已知函数，则____________．
【规律方法】
1.对数函数的解析式同时满足：
①对数符号前面的系数是1；②对数的底数是不等于1的正实数(常数)；③对数的真数仅有自变量x.
2.确定对数函数的解析式，常常利用“待定系数法”.
3.涉及对数函数求函数值问题，有时直接将自变量值代入，有时需先求函数的解析式，再求函数值.
【变式训练】
变式2-1. （2006·辽宁·高考真题）设，则______．
变式2-2. （2022秋·北京·高三北京市第十三中学校考开学考试）已知函数，且.则___________；___________.
变式2-3. （2020·全国·高三对口高考）已知，其中且，若，，则___________．
题型三：对数函数的定义域、值域问题
【典例分析】
例3-1．（2023·全国·高三对口高考）函数的定义域是（ ）
A．B．
C．D．
例3-2．（2022秋·江苏南京·高三校考阶段练习）已知（且），且.
(1)求a的值及的定义域；
(2)求在上的值域.
【方法技巧】
1.确定对数函数或与对数有关的函数定义域，应注意：（1）对数的真数大于零；（2）对数的底数大于零且不等于1；（3）当涉及多方面要求时，注意求“交集”.
2.对数函数的值域问题，往往利用复合函数的单调性.
【变式训练】
变式3-1. 【多选题】（2023·广东·统考模拟预测）已知函数，则（ ）
A．当时，的定义域为R
B．一定存在最小值
C．的图象关于直线对称
D．当时，的值域为R
变式3-2.（2023春·北京东城·高三北京市第十一中学校考阶段练习）函数的定义域为__________．
题型四：对数函数的图象及其应用
【典例分析】
例4-1.（2019浙江高考真题）在同一直角坐标系中，函数且的图象可能是（ ）
A．B．
C．D．
例4-2．（2022秋·福建宁德·高三福建省福安市第一中学校考阶段练习）已知函数且的图象恒过定点，点在幂函数的图象上，则（ ）
A．B．2C．1D．
例4-3．（2023·北京顺义·北京市顺义区第一中学校考模拟预测）已知函数，则不等式的解集为（ ）
A．B．
C．D．
【总结提升】
1.对数函数图象特征：
(1)不管a>1还是0(2)在第一象限内，依图象的分布，逆时针方向a逐渐变小，即a的值越小，图象越靠近y轴．
2.熟记函数图象的分布规律，就能在解答有关对数图象的选择、填空题时，灵活运用图象，数形结合解决．
3．对数值lgax的符号(x>0，a>0且a≠1)规律：“同正异负”．
(1)当01，a>1时，lgax>0，即当真数x和底数a同大于(或小于)1时，对数lgax>0，即对数值为正数，简称为“同正”；
(2)当01或x>1,04．指数型、对数型函数的图象与性质的讨论，常常要转化为相应指数函数，对数函数的图象与性质的问题．
【变式训练】
变式4-1. （2023·安徽安庆·校考一模）函数与在同一直角坐标系下的图象大致是（ ）
A．B．
C．D．
变式4-2.（2023·全国·模拟预测）函数在区间上的大致图象为（ ）
A．B．
C．D．
变式4-3.（2023春·黑龙江哈尔滨·高三哈尔滨市第十三中学校校考开学考试）已知函数．若，且，则的取值范围是（ ）
A．B．C．D．
题型五：对数函数的性质及其应用
【典例分析】
例5-1. （2022·全国·统考高考真题）已知，则（ ）
A．B．C．D．
例5-2.（2022·天津·统考高考真题）已知，，，则（ ）
A．B．C．D．
例5-3．（2023·全国·高三专题练习）已知，若，且的最大值为，则函数的最小值为______
例5-4. （2022秋·重庆·高三统考阶段练习）已知且，函数有最小值，则的取值范围是___________.
【总结提升】
1.比较函数值大小时，要注意区分底数相同还是指数相同．是用指数函数的单调性，还是用幂函数的单调性或指数函数的图象解决．涉及对数值，要注意中间量-1、0、1等的运用．
2.应用对数型函数的图象可求解的问题
(1)在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合思想．
(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．
【变式训练】
变式5-1. （2021·天津·统考高考真题）设，则a，b，c的大小关系为（ ）
A．B．C．D．
变式5-2. （2023·全国·高三专题练习）若函数有最小值，则实数a的取值范围是（ ）
A．B．
C．D．
变式5-3. （2023·全国·高三专题练习）已知函数且，若函数的值域是，则实数的取值范围是（ ）
A．B．
C．D．
变式5-4.（2023·湖南长沙·长郡中学校考模拟预测）已知函数（且），若对任意，，则实数a的取值范围为________．
题型六：对数函数中的恒成立问题
【典例分析】
例6-1.（2022春·江西宜春·高三校联考阶段练习）若，不等式恒成立，则实数的取值范围为___________.
例6-2. （2023·全国·高三对口高考）若函数的定义域为，则a的取值范围为__________；若函数的值域为，则a的取值范围为__________.
【规律方法】
1.当对数的真数为二次函数时，“判别式法”常用于解答“恒成立问题”．
2.“分离参数法”、“分离变量法”常用于解答“恒成立问题”.
【变式训练】
变式6-1.（2022·全国·高三专题练习）若关于的不等式对任意的恒成立，则实数的取值范围是______．
变式6-2. （2023·全国·高三专题练习）已知函数的值域为，则的取值范围是______．
题型七：对数函数的综合问题
【典例分析】
例7-1. （2023·河南开封·校考模拟预测）已知函数，若，则实数的取值范围是（ ）
A．B．
C．D．
例7-2.（2020·全国·统考高考真题）若，则（ ）
A．B．C．D．
例7-3.（2022·全国·统考高考真题）若是奇函数，则_____，______．
例7-4.（2023春·山东淄博·高三山东省淄博实验中学校联考阶段练习）已知函数，若函数恰有4个不同的零点，则的取值范围是__________．
【特别提醒】
应用对数函数的图象和性质，解答与对数函数有关问题，必须弄清三方面的问题：一是定义域，所有问题都必须在定义域内讨论；二是底数与1的大小关系；三是复合函数的构成，即它是由哪些基本初等函数复合而成的．另外，解题时要注意数形结合、分类讨论、转化与化归思想的使用．
【变式训练】
变式7-1. （2022春·江西抚州·高三临川一中校考期中）已知定义在上的函数满足，函数为偶函数，且当时，，则（ ）
A．B．1C．504D．无法确定
变式7-2. （2023·江西南昌·统考三模）设函数，，若存在实数满足：①；②，③，则的取值范围是（ ）
A．B．C．D．
变式7-3. （2023·陕西宝鸡·校考模拟预测）已知函数，若函数有6个不同的零点，且最小的零点为，则（ ）．
A．6B．C．2D．
变式7-4. （2019秋·上海·高三上海市七宝中学校考期末）已知定义在上的函数，设为三个互不相同的实数，满足，则的取值范围为_______.
一、单选题
1．（2023·安徽阜阳·安徽省临泉第一中学校考三模）已知，则（ ）
A．B．
C．D．
2．（2023·广东汕头·统考三模）已知，，，则a，b，c大小为（ ）
A．B．
C．D．
3．（2022秋·江西赣州·高三校联考阶段练习）已知函数，则不等式的解集为（ ）
A．B．
C．D．
4．（2023·全国·高三专题练习）函数的图象可能是（ ）．
A．B．
C．D．
5．（2023·全国·高三专题练习）已知，，，则的最小值为（ ）
A．4B．6C．8D．10
6．（2023·湖南·校联考模拟预测）已知，则下列结论正确的是（ ）
A．B．
C．D．
7．（2023·广东深圳·深圳中学校考模拟预测）已知，，，则（ ）
A．B．C．D．
二、多选题
8．（2023·全国·高三专题练习）已知函数，关于的方程有且只有一个实根，则实数的取值可以是（ ）
A．B．C．D．
9．（2023·全国·高三专题练习）已知函数（a＞0，且）的定义域为，值域为．若的最小值为，则实数a的值可以是（ ）
A．B．C．D．
三、填空题
10．（2023·全国·高三专题练习）命题：“”是真命题，则实数的取值范围为________________.
11．（2023·浙江嘉兴·校考模拟预测）若函数的图象不过第四象限，则实数a的取值范围为________．
12．（2023·全国·高三专题练习）已知函数在内的最大值是最小值的两倍，且，则______
a>1
0图象
性质
定义域：(0，＋∞)
值域：R
当x＝1时，y＝0，即过定点(1，0)
当x>1时，y>0；
当0当x>1时，y<0；
当00
在(0，＋∞)上是增函数
在(0，＋∞)上是减函数