人教版八年级下册第二十章 数据的分析20.2 数据的波动程度优质ppt课件

这是一份人教版八年级下册第二十章 数据的分析20.2 数据的波动程度优质ppt课件，文件包含202《数据的波动程度》课件-人教版数学八年级下册pptx、202方差重难点专项练习四大题型原卷版docx、202方差重难点专项练习四大题型解析版docx等3份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

1.理解方差的意义，学会如何刻画一组数据波动的大小.2.理解方差的计算公式，并会用它来比较两组数据的波动大小解决一些实际问题.3.探索方差产生的过程，发展合情推理的能力.4.能用样本的方差估计总体的方差及根据方差做决策.
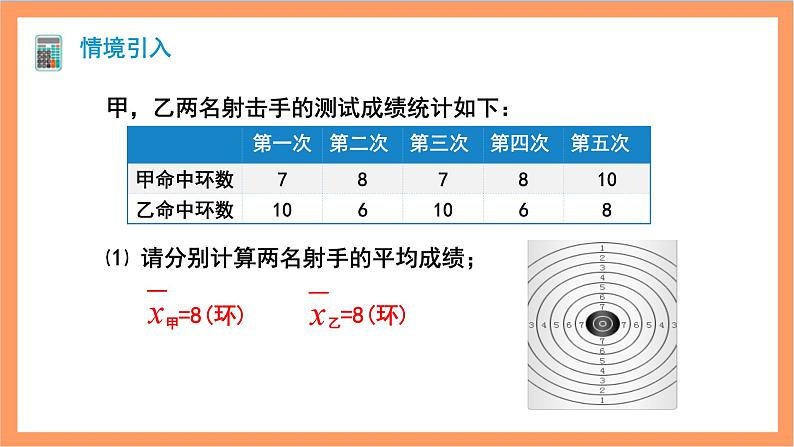
甲，乙两名射击手的测试成绩统计如下：⑴ 请分别计算两名射手的平均成绩；
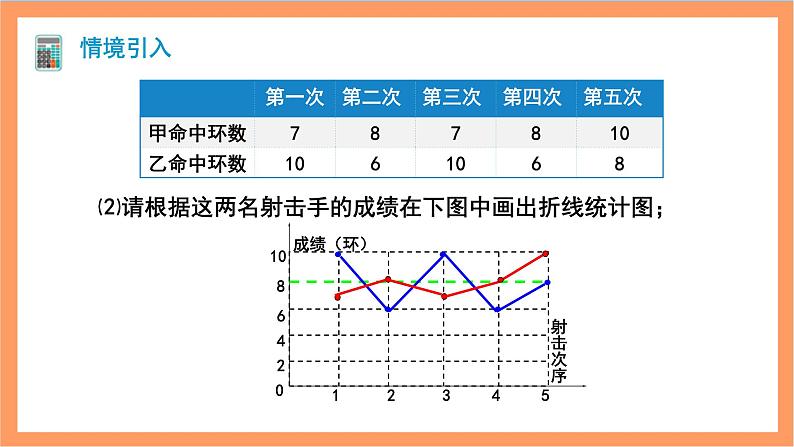
⑵请根据这两名射击手的成绩在下图中画出折线统计图；
思考 甲，乙两名射击手现要挑选一名射击手参加比赛，若你是教练，你认为挑选哪一位比较适宜？
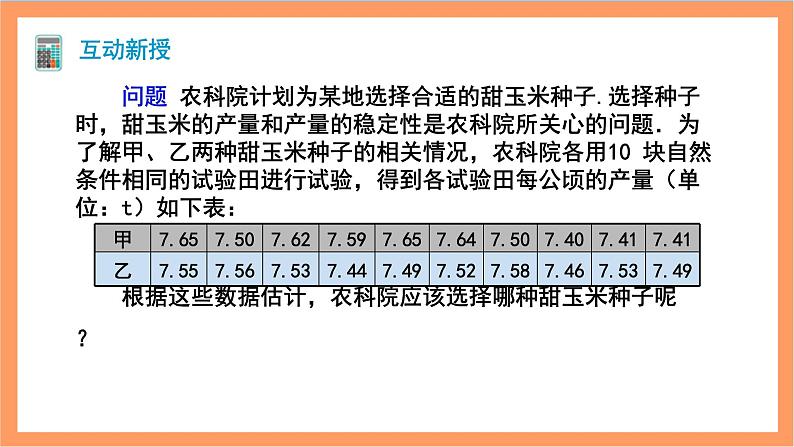
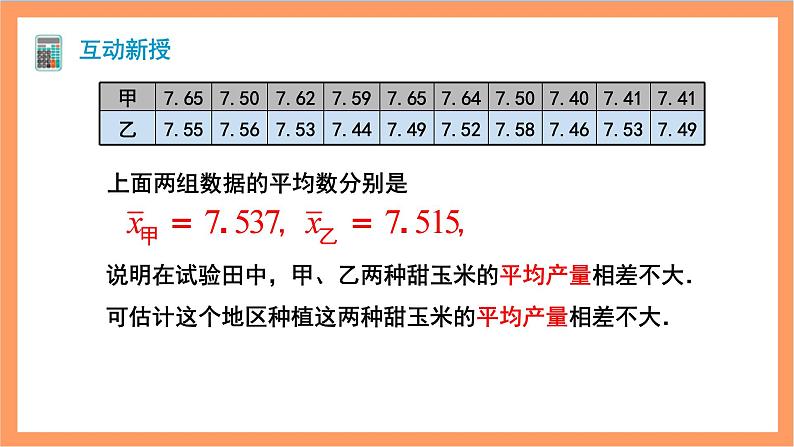
问题 农科院计划为某地选择合适的甜玉米种子.选择种子时，甜玉米的产量和产量的稳定性是农科院所关心的问题．为了解甲、乙两种甜玉米种子的相关情况，农科院各用10 块自然条件相同的试验田进行试验，得到各试验田每公顷的产量（单位：t）如下表：
根据这些数据估计，农科院应该选择哪种甜玉米种子呢？
上面两组数据的平均数分别是
说明在试验田中，甲、乙两种甜玉米的平均产量相差不大．可估计这个地区种植这两种甜玉米的平均产量相差不大．
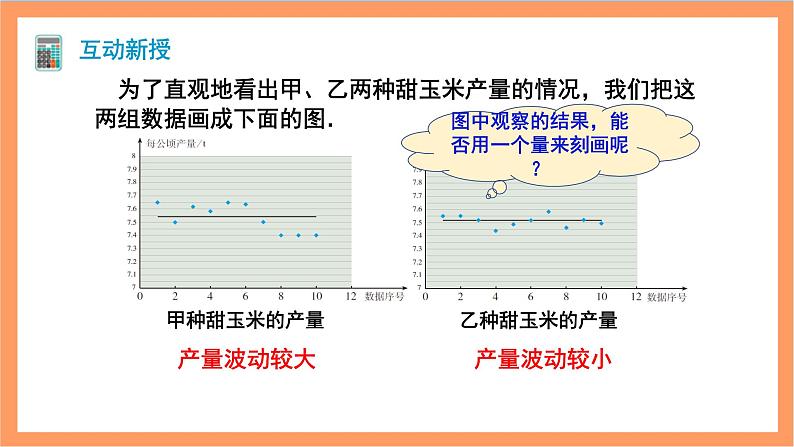
为了直观地看出甲、乙两种甜玉米产量的情况，我们把这两组数据画成下面的图．
图中观察的结果，能否用一个量来刻画呢？
为了刻画一组数据波动的大小，可以采用很多方法.统计中常采用下面的做法： 设有n个数据x1，x2，…，xn，各数据与它们的平均数　 的差的平方分别是 ，我们用这些值的平均数，即用 来衡量这组数据的波动大小，并把它叫作这组数据的方差，记作 ．
方差的意义: 方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小). 方差越大，数据的波动越大； 方差越小，数据的波动越小．
下面我们利用方差来分析甲、乙两种甜玉米的波动程度． 　
两组数据的方差分别是：
例1 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高（单位：cm）如表所示. 哪个芭蕾舞团女演员的身高更整齐？
解：甲、乙两团演员的身高平均数分别是
使用计算器说明：1.不同品牌的计算器的操作步骤有所不同，操作时需要参阅计算器的使用说明书.2.通常需要先按动有关键，使计算器进入统计状态；然后依次输入数据x1，x2，…，xn ；最后按动求方差的功能键（例如 键），计算器便会求出方差 的值.
例2 现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿，两家鸡腿的价格相同，品质相近，快餐公司决定通过检查鸡腿的重量来确定选购哪家公司的鸡腿，检查人员从两家的鸡腿中各抽取15个鸡腿，记录它们的质量如下（单位：g）：根据表中数据，你认为快餐公司应该选购哪家加工厂的鸡腿？
解：甲、乙两家抽取的样本数据的平均数分别是
样本数据的方差分别是：　　　
3.甲乙两名同学本学期参加了相同的5次数学考试，老师想判断这两位同学的数学成绩谁更稳定，老师需比较这两人5次数学成绩的（　　）A．平均数 B．中位数 C．众数 D．方差4.为了比较甲乙两足球队的身高谁更整齐，分别量出每人身高，发现两队的平均身高一样，甲、乙两队的方差分别是1.7、2.4，则下列说法正确的是（　　）A．甲、乙两队身高一样整齐 B．甲队身高更整齐C．乙队身高更整齐 D．无法确定甲、乙两队身高谁更整齐
1.人数相同的八年级（1）、（2）两班学生在同一次数学单元测试中，班级平均分和方差下： 则成绩较为稳定的班级是（ ） A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
2.甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数统计结果如下表： 某同学分析上表后得出如下结论：①甲、乙两班学生成绩平均水平相同；②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀)；③甲班成绩的波动比乙班大.上述结论正确的有 .
3.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛，在相同条件下对他们的电脑知识进行10次测验，成绩（单位：分）如下：
（2）利用以上信息，请从不同的角度对甲、乙两名同学的成绩进行评价.
解：从众数看，甲成绩的众数为84分，乙成绩的众数是90分，乙的成绩比甲好； 从方差看，s2甲=14.4， s2乙=34，甲的成绩比乙相对稳定；从甲、乙的中位数、平均数看，中位数、平均数都是84分，两人成绩一样好； 从频率看，甲85分以上的次数比乙少，乙的成绩比甲好.
1.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛．在最近10次选拔赛中，他们的成绩（单位: cm）如下：甲：585 596 610 598 612 597 604 600 613 601乙：613 618 580 574 618 593 585 590 598 624（1）这两名运动员的运动成绩各有何特点？
由上面计算结果可知：甲队员的平均成绩较好，也比较稳定，乙队员的成绩相对不稳定．但甲队员的成绩不突出，乙队员和甲队员相比比较突出．
（2）历届比赛表明，成绩达到5.96 m就很可能夺冠，你认为为了夺冠应选谁参加这项比赛？如果历届比赛成绩表明，成绩达到6.10 m就能打破纪录，那么你认为为了打破纪录应选谁参加这项比赛．
解：从平均数分析可知，甲、乙两队员都有夺冠的可能．但由方差分析可知，甲成绩比较平稳，夺冠的可能性比乙大． 但要打破纪录，成绩要比较突出，因此乙队员打破纪录的可能性更大，我认为为了打破纪录，应选乙队员参加这项比赛．
方差的统计学意义（判断数据的波动程度）：方差越大（小），数据的波动越大（小）.
方差的作用：比较数据的稳定性
利用样本方差估计总体方差
1.某篮球队对运动员进行3分球投篮成绩测试，每人每天投3分球10次，对甲、乙两名队员在五天中进球的个数统计结果如下： 经过计算，甲进球的平均数为 =8，方差为 ．
（1）求乙进球的平均数和方差；（2）现在需要根据以上结果，从甲、乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员去？为什么？