浙江省杭州市钱塘区2023-2024学年六年级上学期数学期末模拟试卷（三）

这是一份浙江省杭州市钱塘区2023-2024学年六年级上学期数学期末模拟试卷（三），共18页。试卷主要包含了认真填空，慎重选择，仔细计算，综合应用，解决问题等内容，欢迎下载使用。

一、认真填空（每题2分，共16分）
1．14÷ =7： =0.35=21( )= %
2． km的23是15km， 比15km多23km是 km。
3．六（1）班有学生25人，1人请事假，1人请病假，这一天的缺勤率是 。
4．在横线上填上“>”“<”“=”。
125% 0.125 625 28%
4143×89 89 20192020÷9798 20192020
5．45吨大豆可以榨油27吨，那么1吨大豆可以榨油 吨。
6．一根长m米的绳子，如果用去13米，还剩下 米；如果用去它的13，还剩下 米。
7．一个时钟的时针长4cm，当它从12时走到9时，它的尖端走了 cm，时针扫过部分的面积是
cm2。
8．如图，一个小圆沿着一个等边三角形滚动一周，若小圆半径是2cm，三角形边长是10cm，小圆绕三角形滚动一周圆心走过的路线长是 cm。
二、慎重选择（每题2分，共16分）
9．估计下面算式的结果，得数最大的是（ ）。
A．800×（1+13）B．800×（1-13）
C．800÷（1+13）D．800×120%
10．12月7日某学校共有37人请假，包括流感、诺如病毒、意外受伤等情况，校医务室想统计各种原因请假人数比例情况，你建议医务室采用（ ）。
A．条形统计图B．折线统计图C．扇形统计图
11．一个比的前项是18，比值是2，这个比的后项是（ ）
A．9B．14C．4D．16
12．龙湖天街“双十一”一件衣服先降价10%，然后再提价10%，价格比原来（ ）
A．降低了B．提高了C．不变D．不能确定
13．一种盐水有150g，盐和水的比是1：5；如果再加入10g盐，那么盐和盐水的比是（ ）
A．7：32B．1：6C．7：25D．3：18
14．完成一份稿件，甲用13小时，乙用25小时，甲、乙的工作效率比是（ ）。
A．13：25B．5：6C．6：5D．25：13
15．某类玩具按15%的利润率出售，出售价为92元，该类玩具原价是多少元？（ ）。
A．92×（1+15% ）B．92÷（1+15%）
C．92÷（1-15%）D．92× （1-15%）
16．如图：下面说错误的是（ ）。
A．阴影部分面积占整个图形的37.5%
B．阴影部分的面积比空白部分的面积小40%
C．阴影部分面积占整个图形的38
D．空白部分比阴影部分大25
三、仔细计算（共28分）
17．直接写出得数。
18．选择合理的方法计算。
①613÷511×56
②3.7×65+13÷56
③(1115−45+720)÷160
④7÷（79+0.875）
⑤22×34+25×75%-6×0.75-34
⑥37×3536
19．操作题
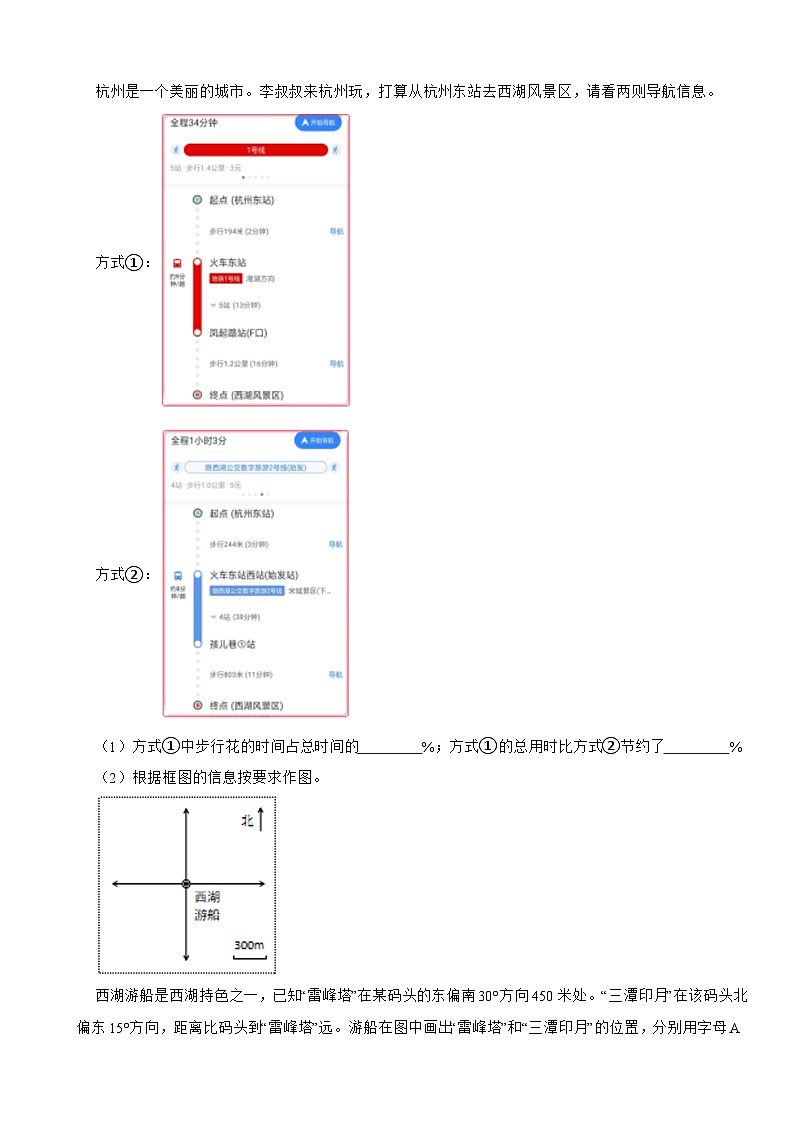
杭州是一个美丽的城市。李叔叔来杭州玩，打算从杭州东站去西湖风景区，请看两则导航信息。
方式①：
方式②：
（1）方式①中步行花的时间占总时间的 %；方式①的总用时比方式②节约了 %
（2）根据框图的信息按要求作图。
西湖游船是西湖持色之一，已知“雷峰塔”在某码头的东偏南30°方向450米处。“三潭印月”在该码头北偏东15°方向，距离比码头到“雷峰塔”远。游船在图中画出“雷峰塔”和“三潭印月”的位置，分别用字母A和B表示．
四、综合应用（共16分）
20．浙江省各地积极践行垃圾分类活动。
（1）所有垃圾一共有 吨，有害垃圾C类占垃圾总数的 %；
（2）B类垃圾的吨数是 ；
（3）请将条形统计图补充完整；
（4）据统计，可回收垃圾中的1吨废塑料可回炼600kg的柴油。如果此次可回收垃圾中的20%是废弃塑料，那么可以回炼 千克柴油。
21．如图，如果钟面上的12时作为正北方向，那么7时可描述为 偏 、 °的方向， 时为东偏北30°。
22．下图A、B两阴影部分的面积相等。
（1）A、B两阴影部分的面积和是 cm。
（2）比较A、B两部分阴影部分的周长，则CA CB（填“>”或者“<”）。
23．按下面用小棒摆正六边形。摆4个正六边形需要 根小棒；摆10个正六边形需要 根小棒；摆n个正六边形需要 根小棒。
24．某商品的售价是60元，比原来的定价便宜了20%，求比原来的定价便宜了多少元？正确的算式是（ ）。
A．60÷（1-20%）-60B．60÷（1-20%）
C．60-60÷（1-20%）D．60×（1-20%）
五、解决问题（每题4分，共24分）
25．一根绳子，剪掉全长的25，剩下的还有1.8米，这根绳子全长多少米？
26．服装厂生产一批校服，已经完成了总套数的13，如果再生产300套，已完成的与剩下的套数比是2：3。这批校服有多少套？
27．一项工程，两队合作12天完成。甲队独做4天完成了这项工程的15，乙队再独做几天可以完成这项工程？
28．有一个环形跑道，它由两条直道和两条半圆形跑道组成，直道长50m，每条跑道宽为1.25米（如图）。淘淘在这个跑道上进行200m赛跑，那么第3道的起跑线与第1道相差多少米？ （ π取3.14）
29．买一台电脑；分期付款购买要加价6%如果一次性付清可按原价的98%成交，刘老师算了算，发现分析付款比一次性付清多付300元，这台电脑原价多少元？
30．有甲、乙两个粮库，原来甲粮库存粮的吨数是乙粮库的57。如果从乙粮库调6吨粮食到甲粮库，那么甲粮库存粮的吨数就是乙粮库的45。原来甲、乙粮库各存粮食多少吨？（列方程解决问题）
答案解析部分
1．【答案】40；20；60；35
【知识点】百分数与小数的互化；比与分数、除法的关系
【解析】【解答】解：因为14÷0.35=40，所以14÷40=0.35；
因为7÷0.35=20，所以7：20=0.35；
因为21÷0.35=60，所以2160=0.35；
0.35=35%
故答案为：40；20；60；35。
【分析】在除法里，已知被除数和商，要求除数，被除数÷商=除数；
在比里，已知比的前项和比值，要求后项，比的前项÷比值=后项；
在分数里，已知分子与分数值，要求分母，分子÷分数值=分母；
小数化成百分数：只要把小数点向右移动两位，同时在后面添上百分号。
2．【答案】22.5；1523
【知识点】除数是分数的分数除法
【解析】【解答】解：15÷23=22.5（km）；
15+23=1523（km）。
故答案为：22.5；1523。
【分析】已知一个数的几分之几是多少，要求这个数，用除法计算；
求比一个数多几的数是多少，用加法计算。
3．【答案】8%
【知识点】百分数的应用--求百分率
【解析】【解答】解：（1+1）÷25×100%
=2÷25×100%
=0.08×100%
=8%
故答案为：8%。
【分析】此题主要考查了百分率的应用，缺勤率=缺勤的人数÷总人数×100%，据此列式解答。
4．【答案】>；<；<；>
【知识点】分数与分数相乘；除数是分数的分数除法；百分数与小数的互化；百分数与分数的互化；商的变化规律；积的变化规律
【解析】【解答】解：因为125%=1.25，1.25＞0.125，所以125%＞0.125；
因为625=6÷25=0.24，28%=0.28，0.24＜0.28，所以625＜28%；
因为4143＜1，所以4143×89＜89；
因为9798＜1，所以20192020÷9798＞20192020。
故答案为：＞；＜；＜；＞。
【分析】比较百分数和小数的大小，先将百分数化成小数，把百分数化成小数，只要把百分号去掉，同时把小数点向左移动两位，然后比较大小；
比较分数和百分数的大小，可以把分数和百分数化成小数，再比较大小，分数化成小数：用分子除以分母，能除尽的就化成有限小数，有的不能除尽，不能化成有限小数的，一般保留三位小数；把百分数化成小数，只要把百分号去掉，同时把小数点向左移动两位；
在乘法里，一个非0数乘小于1的非0数，积小于这个数；一个非0数乘大于1的数，积大于这个数，据此比较大小；
在除法里，一个非0数除以小于1的非0数，商大于被除数；一个非0数除以大于1的数，商小于被除数，据此解答。
5．【答案】514
【知识点】除数是分数的分数除法
【解析】【解答】解：27÷45=514（吨）
故答案为：514。
【分析】根据题意可知，榨油的总吨数÷大豆的质量=1吨大豆可以榨油的质量。
6．【答案】m-13；23m
【知识点】分数乘法与分数加减法的混合运算
【解析】【解答】解：剩下：m-13（米）；
m×（1-13）
=m×23
=23m（米）
故答案为：m-13；23m。
【分析】根据题意可知，绳子的长度-用去的长度=还剩下的长度；把这根绳子的总长度看作单位“1”，这条绳子的总长度×（1-13）=剩下的长度。
7．【答案】18.84；37.68
【知识点】圆的周长；圆的面积
【解析】【解答】解：3.14×4×2×34
=25.12×34
=18.84（cm）
3.14×42×34
=3.14×16×34
=50.24×34
=37.68（cm2）
故答案为：18.84；37.68。
【分析】时针从12时走到9时，它的尖端走过的痕迹是圆周长的34，圆的周长C=2πr；
时针扫过部分的面积是圆面积的34，圆的面积S=πr2。
8．【答案】42.56
【知识点】圆的周长
【解析】【解答】解：3.14×2×2+10×3
=12.56+30
=42.56（cm）
故答案为：42.56。
【分析】观察图可知，小圆绕三角形滚动一周圆心走过的路线长度=小圆的周长+等边三角形的周长。
9．【答案】A
【知识点】分数乘法与分数加减法的混合运算；分数除法与分数加减法的混合运算；含百分数的计算；商的变化规律；积的变化规律
【解析】【解答】选项A，800×（1+13）=800×43>800；
选项B，800×（1-13）=800×23<800；
选项C，800÷（1+13）=800÷43<800；
选项D，800×120%=800×65>800；
因为B、C的结果都小于800，所以比较选项A、D的结果；
又因为43>65，所以800×（1+13）>800×120%。
故答案为：A。
【分析】 一个数（0和负数除外）除以小于1的数，所得的商大于原来的数；反之，商小于原来的数。
一个数（0和负数除外）乘小于1的数，所得的积小于原来的数；反之，积大于原来的数。
10．【答案】C
【知识点】统计图的选择
【解析】【解答】解：要知道因各种原因请假人数比例情况，应采用扇形统计图。
故答案为：C。
【分析】条形统计图特点：可以清楚地看出数量的多少；折线统计图特点：不但可以表示数量的多少，还可以清楚的看出数量的增减变化情况；扇形统计图特点：可以看出各个部分数量与总数之间的关系。据此结合题意选择合适的统计图。
11．【答案】A
【知识点】比的化简与求值
【解析】【解答】解：18÷2=9
故答案为：A。
【分析】已知前项和比值，要求后项，前项÷比值=后项。
12．【答案】A
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：假设原价是“1”，
1×（1-10%）×（1+10%）
=1×90%×110%
=0.99
0.99＜1，降低了。
故答案为：A。
【分析】此题主要考查了百分数的应用，假设原价是“1”，原价×（1-10%）×（1+10%）=现价，然后对比即可。
13．【答案】A
【知识点】比的应用
【解析】【解答】解：150×15+1=25（g）
（25+10）：（150+10）
=35：160
=（35÷5）：（160÷5）
=7：32
故答案为：A。
【分析】已知盐水的质量与盐和水的比，可以求出盐的质量，然后用原来的盐+加入的盐的质量=现在盐的质量，现在盐的质量：（原来盐水的质量+加入的盐的质量）=现在盐和盐水的比，据此化简比。
14．【答案】C
【知识点】比的化简与求值
【解析】【解答】解：把工作总量看作单位“1”，
甲的工效：1÷13=3，
乙的工效：1÷25=52，
3：52=（3×2）：（52×2）=6：5
故答案为：C。
【分析】此题主要考查了工程应用题，把工作总量看作单位“1”，工作总量÷工作时间=工作效率，分别求出甲、乙的工作效率，然后用甲的工效与乙的工效相比，据此化简比。
15．【答案】B
【知识点】百分数的应用--利润
【解析】【解答】解：把原价看作单位“1”，求原价，用92÷（1+15%）。
故答案为：B。
【分析】此题主要考查了利润的知识，把原价看作单位“1”，原价×（1+利润率）=售价，要求原价，用除法计算。
16．【答案】D
【知识点】百分数的意义与读写；百分数的应用--增加或减少百分之几
【解析】【解答】选项A，3÷8=0.375=37.5%，原题说法正确；
选项B，（5-3）÷5=40%，原题说法正确；
选项C，3÷8=38，原题说法正确；
选项D，（5-3）÷3=23，原题说法错误。
故答案为：D。
【分析】观察图可知，把长方形平均分成8份，其中阴影部分占其中的3份，空白部分占其中的5份，据此解答。
17．【答案】
【知识点】除数是分数的分数除法；分数除法与分数加减法的混合运算；含百分数的计算；比的化简与求值
【解析】【分析】分数与小数相乘，先约分，再计算；
含百分数的计算，可以把百分数化成分数或小数，再计算；
一个算式中有除法和加法，先算除法，后算加法；
分数比的化简：比的前项和后项同时乘分母的最小公倍数，如果还不是最简比，再同时除以相同的数变为最简比；
分数除法的计算法则：甲数除以乙数（0除外），等于甲数乘乙数的倒数，据此解答。
18．【答案】解：①613÷511×56
=613×115×56
=1113
②3.7×65+13÷56
= 3.7×65+1.3×65
=(3.7+1.3)×65
= 5×65
=6
③(1115−45+720)÷160
=(1115−45+720)× 60
=1115× 60-45×60+720× 60
=44-48+21
=44+21-48
=65-48
= 17
④7÷(79 +0.875)
= 7÷(79+78)
= 7÷(5672+6372)
= 7÷11972
=7×72119
=7217
⑤22×34+25×75%-6×0.75-34
=22×34+25×34-6×34-34×1
=(22+25-6-1)×34
=40×34
=30
⑥37×3536
=(36 +1)×3536
=36×3536+3536
=353536
【知识点】分数四则混合运算及应用；含百分数的计算；分数乘法运算律
【解析】【分析】①观察数据可知，先把除法变成乘法，再约分计算；
②观察数据可知，先把除法变成乘法，再利用乘法分配律简算；
③观察数据可知，先把除法变成乘法，再利用乘法分配律简算；
④观察算式可知，算式中有小括号，先算小括号里面的加法，再计算小括号外面的除法；
⑤观察数据可知，先把百分数、小数化成分数 ，再利用乘法分配律简算；
⑥观察数据可知，先把37分成（36+1），再利用乘法分配律简算。
19．【答案】（1）52.9；46.0
（2）解：根据分析，作图如下：
【知识点】根据方向和距离确定物体的位置；百分数的应用--增加或减少百分之几
【解析】【解答】解：（1）（2+16）÷34
=18÷34
≈0.529
=52.9%
1小时3分=63分
（63-34）÷63
=29÷63
≈0.460
=46.0%
故答案为：（1）52.9；46.0。
【分析】（1）方式①步行的时间÷总时间=步行花的时间占总时间的百分比；
（方式②用的时间-方式①的时间）÷方式②的时间=方式①的总用时比方式②节约了百分之几；
（2）观察图可知，此图是按“上北下南，左西右东”来规定方向的，图上距离1厘米表示实际距离300米，根据方向和距离，找出“雷峰塔”和“三潭印月”的位置，分别用字母A和B表示。
20．【答案】（1）50；6
（2）15吨
（3）
（4）3240
【知识点】从扇形统计图获取信息；百分数的应用--运用乘法求部分量
【解析】【解答】解：（1）5÷10%=50（吨）；
1-（54%+10%+30%）
=1-94%
=6%
（2）50×30%=15（吨）；
（3）补充统计图如下：
（4）50×54%=27（吨）；
27×20%=5.4（吨）；
5.4×600=3240（千克）。
故答案为：（1）50；6；（2）15吨；（4）3240。
【分析】（1）观察条形统计图可知，D类垃圾有5吨，观察扇形统计图可知，D类垃圾占垃圾总量的10%，D类垃圾的质量÷10%=垃圾的总量；
把垃圾的总量看作单位“1”，单位“1”-（A类垃圾占总量的百分比+B类垃圾占总量的百分比+D类垃圾占总量的百分比）=有害垃圾C类占垃圾总数的百分比；
（2）垃圾的总量×B类垃圾占总量的百分比=B类垃圾的质量；
（3）观察条形统计图可知，纵轴每格代表5吨，由此绘制B类垃圾的条形即可；
（4）根据题意可知，先求出可回收垃圾的质量，然后求出可回收垃圾中废弃塑料的质量，最后用废弃塑料的质量×每吨废弃塑料可以回炼的柴油质量=一共可以回炼的柴油质量，据此列式解答。
21．【答案】南；西；30；2
【知识点】根据方向和距离描述路线图
【解析】【解答】解：观察图可知，每大格所对应的圆心角是30°， 如果钟面上的12时作为正北方向，那么7时可描述为南偏西、30°的方向，1时为东偏北30° 。
故答案为：南；西；30；2。
【分析】根据条件“如果钟面上的12时作为正北方向”可知，图中是按“上北下南，左西右东”来规定方向的，钟面被12个数字平均分成12大格，每个大格所对的圆心角是360°÷12=30°，据此描述位置。
22．【答案】（1）471
（2）＞
【知识点】组合图形面积的巧算；圆的周长；圆的面积
【解析】【解答】解：（1）3.14×102×34×2
=3.14×100×34×2
=314×34×2
=235.5×2
=471（cm2）
（2）3.14×102×34
=314×34
=235.5（cm2）
235.5÷10=23.55（cm）
阴影部分A的周长：
3.14×10×2×34+10×2
=47.1+20
=67.1（cm）
阴影部分B的周长：
3.14×10×2×14+23.55+10+（23.55-10）
=15.7+23.55+10+13.55
=39.25+10+13.55
=49.25+13.55
=62.8（cm）
67.1＞62.8， CA＞CB。
故答案为：（1）471；（2）＞。
【分析】（1）阴影部分A的面积等于圆面积的34，据此列式计算，已知A、B两阴影部分的面积相等，直接乘2即可得到两个阴影部分的面积和；
（2）根据题意，分别求出两个阴影部分的周长，再对比即可。
23．【答案】21；51；5n+1
【知识点】数形结合规律
【解析】【解答】解：摆1个正六边形需要：5×1+1=6根小棒，
摆2个正六边形需要：5×2+1=11根小棒，
摆3个正六边形需要：5×3+1=16根小棒，
摆4个正六边形需要：5×4+1=21根小棒，
……
摆10个正六边形需要：5×10+1=51根小棒，
摆n个正六边形需要：5×n1+1=5n+1根小棒。
故答案为：21；51；5n+1。
【分析】此题主要考查了数形结合的知识，观察图形可得规律：摆n个正六边形需要5n+1根小棒。
24．【答案】A
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：把原价看作单位“1”，求原价：60÷（1-20%），
比原来便宜：60÷（1-20%）-60。
故答案为：A。
【分析】此题主要考查了百分数的应用，把原价看作单位“1”，先求出原来的定价，售价÷（1-20%）=原来的定价，原来的定价-现在的售价=现在比原来的定价便宜的钱数。
25．【答案】解：1.8÷(1-25)
=1.8÷35
=3(米)
答：这根绳子全长3米。
【知识点】分数除法与分数加减法的混合运算
【解析】【分析】根据题意可知，把这根绳子的总长看作单位“1”，剩下的长度÷剩下的占全长的分率=绳子的全长，据此列式解答。
26．【答案】解：300÷(23+2−13)
=300÷115
=4500(套)
答：这批校服有4500套。
【知识点】比的应用
【解析】【分析】根据题意可知，把总套数看作单位“1”，求出生产的300套的对应分率是关键，生产的300套÷（现在已完成的占总套数的分率-原来完成的占总套数的分率）=这批校服的总套数，据此列式解答。
27．【答案】解：(1-15)÷(112−15÷4)
=45÷130
=24(天)
答：乙队再独做24天可以完成这项工程。
【知识点】工程问题；分数除法与分数加减法的混合运算
【解析】【分析】此题主要考查了工程应用题，把这项工程的总量看作单位“1”，工作总量÷工作时间=工作效率，（这项工程的总量“1”-甲队单独完成的分率）÷（两队的工作效率和-甲队的工效）=乙队单独需要做的天数，据此列式解答。
28．【答案】解：3.14×1.25× (3-1) ×2
=3.14×1.25×2×2
=3.925×2×2
=7.85×2
=15.7 (米)
答：那么第3道的起跑线与第1道相差15.7米．
【知识点】圆的周长
【解析】【分析】在确定起跑线的应用题中，环形跑道的直道长度是相等的，相邻跑道起跑线相差的距离=π×跑道宽度，据此列式解答。
29．【答案】解：1-98%=2%
300÷(6%+2%)
=300÷8%
=3750(元)
答：这台电脑原价3750元。
【知识点】百分数的其他应用
【解析】【分析】根据题意可知，这台电脑分期多付的钱数÷（分期需要加价的百分比+分期时比一次性付清多付的百分比）=这台电脑原价，据此列式解答。
30．【答案】解：设原来乙粮库有粮食x吨
(x-6)×45=57x+6
45x-57x=6+245
335x=545
x=126
126×57=90 (吨)
答：原来甲粮库存粮90吨，乙粮库存粮126吨。
【知识点】列方程解关于分数问题
【解析】【分析】此题主要考查了列方程解决问题，设原来乙粮库有粮食x吨，（乙粮库原来的粮食质量-调出的吨数）×45=原来甲粮库的存粮质量+调入的吨数，据此列方程解答。43×1.2=
10÷25% =
16+16÷16+16=
（ ）： 47=47
1÷43=
0.45+120=
67÷27=
78千克：375克=
43×1.2=1.6
10÷25% =40
16+16÷16+16=43
43： 47=73
1÷43=34
0.45+120=12
67÷27=3
78千克：375克=73