初中数学华师大版八年级上册第14章 勾股定理14.2 勾股定理的应用教课内容课件ppt

这是一份初中数学华师大版八年级上册第14章 勾股定理14.2 勾股定理的应用教课内容课件ppt，共25页。PPT课件主要包含了逐点学练，本节小结，作业提升，学习目标，本节要点，学习流程，知识点，感悟新知，勾股定理的应用，实际问题等内容，欢迎下载使用。
确定几何体表面上两点间的最短路线长勾股定理的应用
确定几何体表面上两点间的最短路线长
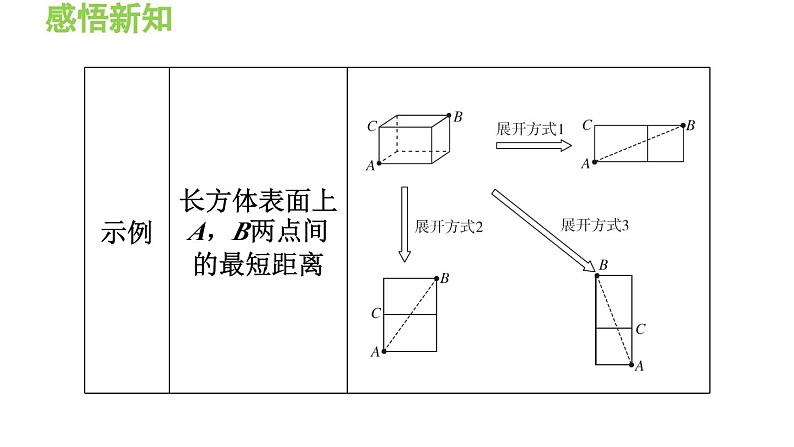
1. 求长方体表面上两点间的最短路线长的方法(1)将长方体的表面展开成平面图形，展开时要考虑各种可能的情况；(2)在各种可能的情况中，分别确定两点的位置并连结成线段；(3)利用勾股定理分别求每种情况中线段的长度；(4)对各线段长度进行比较，长度最短的线段为最短路线.
2. 求圆柱体侧面上两点间的最短路线长的方法(1)将圆柱体的侧面展开，确定两点的位置，连结两点的线段即为最短路线；(2)构造直角三角形，利用勾股定理求其长度.
特别解读1. 在平面上寻找两点之间的最短路线的依据：(1)两点之间线段最短；(2)直线外一点到直线上所有点的连线中，垂线段最短.2. 在立体图形中，由于受到物体和空间的阻隔，两点间的最短路线长不一定是两点间的线段长.3. 确定立体图形上的最短路线，需要先将立体图形展开成平面图形，再构造直角三角形进行计算，最后通过比较得出最短路线.
如图14.2-1，圆柱体的高为40 cm，底面周长为60 cm，一只蚂蚁从点A 出发，沿着圆柱体的侧面爬到点B，然后另找一条路线爬回点A，求蚂蚁爬行的最短路线的长度.
解题秘方：先利用展开图确定最短路线，再利用勾股定理求路线长.
解：将圆柱体的侧面展开如图14.2-2，连结AB、A′B.在Rt △ ABC 中，BC=40 cm，AC= AA′= =30(cm)，由勾股定理得AB= =50(cm).同理可得A′B=50 cm，则最短路线的长度为AB+A′B=50+50=100(cm).答：蚂蚁爬行的最短路线的长度为100 cm.
1-1. 如图，长方体的底面两条边长分别为1 cm和3 cm，高为6 cm. 如果用一根细线从点A 开始经过4 个侧面缠绕一圈到达点B，那么所用细线最短需要________cm.
1.勾股定理的应用范围 勾股定理是直角三角形的一个重要性质，它把直角三角形有一个直角的“形”的特点转化为三边“数”的关系. 利用勾股定理，可以解决与直角三角形有关的计算和证明问题，还可以解决生活、生产中的一些实际问题.
2. 勾股定理应用的常见类型(1)已知直角三角形的任意两边求第三边；(2)已知直角三角形的任意一边确定另两边的关系；(3)证明包含有平方(算术平方根)关系的几何问题；(4)求解几何体表面上的最短路程问题；(5)构造方程(或方程组)计算有关线段长度，解决生产、生活中的实际问题.
特别提醒运用勾股定理解决实际问题的一般步骤：1. 从实际问题中抽象出几何图形；2. 确定要求的线段所在的直角三角形；3. 找准直角边和斜边，根据勾股定理建立等量关系；4. 求得结果.
如图14.2-3， 在Rt△ABC 中，∠ACB=90 °，AC=3，BC=4，CD⊥ AB，垂足为D. 求CD的长.
解题秘方：紧扣“直角三角形的面积的两种表示法”求解.
解：∵∠ ACB=90°，AC=3，BC=4，∴ AB=∵ CD ⊥ AB，∴S△ABC= AB·CD= AC·BC.∴ AB·CD=AC·BC.∴ CD=
2-1. 如图，在△ABC中，∠B=40°，EF∥AB，∠1=50°，CE=3，EF比CF 大1，则EF的长为( )A. 5 B. 6 C. 3 D. 4
如图14.2－4，在Rt △ ABC 中，∠ C=90°，AM是中线，MN ⊥ AB，垂足为N. 求证：AN2－BN2=AC2.
解题秘方：将要证明的线段归结到不同的直角三角形中，结合等式性质证明.
证明：∵ MN ⊥ AB，∴在Rt △ AMN 中，AN2+MN2=AM2，在Rt △ BMN 中，BN2+MN2=MB2.∴ AN2－BN2=AM2－MB2.在Rt △ AMC 中，∵∠ C=90°，∴ AM2－MC2=AC2.∵ AM 是中线，∴ MC=MB.∴ AM2－MB2=AC2. ∴ AN2－BN2=AC2.
3-1. 如图，在Rt △ ABC中， ∠ C=90 °，AM=CM，MP ⊥ AB 于点P.求证：BP2=BC2+AP2.
证明：连结BM.∵PM⊥AB，∴△BMP和△AMP均为直角三角形．∴BP2＋PM2＝BM2，AP2＋PM2＝AM2.同理可得BC2＋CM2＝BM2，∴BP2＋PM2＝BC2＋CM2.又∵CM＝AM，∴CM2＝AM2＝AP2＋PM2.∴BP2＋PM2＝BC2＋AP2＋PM2.∴BP2＝BC2＋AP2.
一架长5 m 的梯子，斜靠在一竖直墙上，这时梯子的底端距墙脚3 m，若梯子的顶端下滑1 m，则梯子的底端将滑动( )A.0 m B.1 m C.2 m D.3 m
解题秘方：将实际应用问题通过建模转化为直角三角形的问题求解.
解：根据题意，建立如图14.2-5 的模型，BB1 的长即为所求.在Rt △ ABC 中，∠ ACB=90°，AB=5 m，BC=3 m，∴ AC= =4(m).在Rt △ A1B1C 中，∠ A1CB1=90°，A1C=AC－AA1=4－1=3(m)，A1B1=5 m，∴ B1C= =4(m).∴ BB1=B1C－BC=4－3=1(m).
4-1. 古诗赞美荷花“竹色溪下绿， 荷花镜里香”. 平静的湖面上，一朵荷花亭亭玉立，露出水面10 cm，忽见它随风斜倚，花朵恰好浸入水面，仔细观察，发现荷花偏离原地40 cm(如图). 请问： 水深多少？
解：设水深CB＝x cm，则AC＝(x＋10) cm，即CD＝(x＋10) cm.在Rt△BCD中，由勾股定理得x2＋402＝(x＋10)2，解得x＝75.答：水深75 cm.