


备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题11 函数的零点【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版
展开一、考向解读
考向:函数的零点问题一般以选择题或者填空题的形式出现,注意考查定义,方法中定义法和数形结合的思想用的较多。有时候也会在解答题中出现,主要是结合导数考查,一般是压轴题了。
考点:函数的零点与方程的根
导师建议:数形结合是零点问题的重难点!
二、知识点汇总
一、函数的零点与方程的根
1、定义:如果函数在实数处的值等于零,即,则叫做这个函数的零点.
2、等价定义
(1)函数的零点也就是函数的图象与轴交点的横坐标;
(2)函数的零点就是方程的实数根.
二、零点存在定理
1、定理:如果函数在区间上的图象是一条连续不断的曲线,且,
那么,函数在区间内至少有一个零点,即存在,使得。
2、函数在区间上的图象是一条连续不断的曲线,,且具有单调性,则函数在区间内只有一个零点.
三、函数零点个数判断的一般方法
1、直接法:直接求零点,令,求出它的解,但是要注意零点是否有相同的部分.
2、定理法:利用零点存在定理,函数的图象在区间上是连续不断的曲线,且,
结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.
3、图象法:
(1)单个函数图象:利用图象交点的个数,画出函数的图象,函数的图象与轴交点的个数就是函数的零点个数;
(2)两个函数图象:将函数拆成两个函数和的差,根据,则函数的零点个数就是函数和的图象的交点个数
【常用结论】
1.方程有实数根函数的图象与轴有交点函数有零点.
2.零点不是点喔,是一个数!(偷偷告诉你,极值点也不是点,是数来着)
三、题型专项训练
①求函数的零点
一、单选题
1.已知函数,则的零点为( )
A.和B.和
C.和D.和
2.已知函数则函数的零点的个数为( )
A.0B.1
C.2D.3
3.函数的零点是( )
A.1B.C.D.4
4.函数的零点为( )
A.4B.4或5C.5D.或5
②比较零点的大小关系
5.设方程的两个根为,则
A.B.C.D.
6.已知函数,,的零点分别为a,b,c,则( )
A.B.C.D.
7.已知是自然对数的底数,函数的零点为,函数的零点为,则下列不等式中成立的是
A.B.C.D.
③求零点的和
8.已知函数,则的所有零点之和为( )
A.B.C.D.
9.函数的零点之和为( )
A.-1B.1C.-2D.2
10.函数与,两函数图象所有交点的横坐标之和为( ).
A.0B.2C.3D.4
11.函数在上的所有零点之和为( )
A.B.C.D.
12.函数在区间上的所有零点之和等于( )
A.B.0C.3D.2
④根据零点个数求参数范围
13.若方程有两个不同的实数根,则实数的取值范围为( )
A.B.C.D.
14.已知函数,若函数有两个不同的零点,则实数的取值范围是( )
A.B.
C.D.
15.设,若有三个不同的实数根,则实数a的取值范围是( )
A.B.C.D.
16.若函数在区间内仅有1个零点,则的取值范围是( )
A.B.C.D.
17.已知函数(),若在上有两个零点,则的取值范围是( )
A.B.
C.D.
⑤判断零点所在区间
18.函数的零点所在区间是( )
A.B.C.D.
19.已知方程的解在内,则( )
A.0B.1C.2D.3
20.在下列区间中,函数的零点所在区间为( )
A.(0,1)B.(1,2)C.(2,3)D.(3,4)
21.函数的零点所在的区间为( )
A.(0,1)B.(1,2)C.(2,3)D.(3,4)
22.函数,则的零点所在区间为( )
A.B.C.D.
23.函数在区间上的零点所在的区间为( )
A.B.C.D.
二、多选题
24.已知函数,则以下结论正确的是( )
A.
B.函数是定义域上的增函数
C.函数有个零点
D.方程有两个实数解
25.已知函数,下列结论中正确的是( )
A.是的极小值点
B.有三个零点
C.曲线与直线只有一个公共点
D.函数为奇函数
26.已知函数的零点为,函数的零点为,则下列不等式中成立的是( )
A.B.
C.D.
27.已知函数,的零点分别为,,则( )
A.B.C.D.
28.已知是定义在R上的奇函数,当时,,若关于x的方程恰有4个不相等的实数根,则这4个实数根之和为( )
A.4B.C.D.8
29.已知函数,,则下列说法正确的是( )
A.当时,函数有3个零点
B.当时,若函数有三个零点,则
C.若函数恰有2个零点,则
D.若存在实数m使得函数有3个零点,则
30.已知,若恰有3个零点,则的可能值为( )
A.0B.1C.D.2
31.已知函数,若关于x的方程恰有两个互异的实数解,则实数a的值可以是( )
A.0B.1C.D.2
32.设函数,若关于x的方程有四个实根(),则下列结论正确的是( )
A.B.
C.D.的最小值为16
四、高考真题及模拟题精选
一、单选题
1.(2022·北京延庆·统考模拟预测)已知函数,且,则的零点个数为( )
A.个B.个C.个D.个
2.(2021·陕西西安·西安中学校考模拟预测)已知函数,则函数的零点个数为( ).
A.1B.2C.3D.4
3.(2021·浙江台州·统考二模)若函数在上有两个不同的零点,则的取值范围是( )
A.B.
C.D.
4.(2021·重庆·校联考三模)已知函数,,的零点分别为,,,则,,的大小为( )
A.B.C.D.
5.(2021·天津·统考高考真题)设,函数,若在区间内恰有6个零点,则a的取值范围是( )
A.B.
C.D.
6.(2020·广东中山·校联考模拟预测)定义域为的函数,若关于的方程恰有3个不同的实数解,,,则( )
A.1B.2C.D.
7.(2020·天津·统考高考真题)已知函数若函数恰有4个零点,则的取值范围是( )
A.B.
C.D.
二、多选题
8.(2022·河北石家庄·石家庄二中校考模拟预测)设函数,若关于的方程有四个实数解,且,则的值可能是( )
A.0B.1C.99D.100
9.(山东省临沂市2022-2023学年高一上学期期末数学试题)已知函数,令,则( )
A.若有1个零点,则或
B.若有2个零点,则或
C.的值域是
D.若存在实数a,b,c()满足,则的取值范围为(2,3)
10.(2022·全国·模拟预测)已知函数,若存在三个实数,使得,则( )
A.的取值范围为B.的取值范围为
C.的取值范围为D.的取值范围为
11.(2022·天津·统考高考真题)设,对任意实数x,记.若至少有3个零点,则实数的取值范围为______.
12.(2021·北京·统考高考真题)已知函数,给出下列四个结论:
①若,恰 有2个零点;
②存在负数,使得恰有1个零点;
③存在负数,使得恰有3个零点;
④存在正数,使得恰有3个零点.
其中所有正确结论的序号是_______.
13.(2022·北京·统考高考真题)若函数的一个零点为,则________;________.
五、题型精练,巩固基础
一、单选题
1.(2021·四川成都·统考二模)下列函数在区间内有零点且单调递增的是( )
A.B.C.D.
2.(2020·黑龙江哈尔滨·哈九中校考三模)下列函数在其定义域内,既是奇函数又存在零点的是( )
A.B.
C.D.
3.(2022·安徽合肥·合肥一中校考模拟预测)已知函数,则函数的零点为( )
A.B.,0C.D.0
4.(2021·云南·校联考模拟预测)函数在上的零点个数为( )
A.2B.3C.4D.5
5.(2020·浙江·模拟预测)已知函数有两个零点,,则“”是“”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件
6.(2022·重庆沙坪坝·重庆南开中学校考模拟预测)已知实数a,b,c满足,则下列不等式一定不成立的为( )
A.B.C.D.
7.(2017·辽宁大连·大连八中校考一模)已知函数的零点依次为,则
A.B.C.D.
8.(2022·江西萍乡·统考二模)已知函数,则的所有零点之和为( )
A.B.C.D.
9.(2021·山东济宁·统考二模)已知函数,若,则的最小值是( )
A.B.C.D.
10.(2022·新疆克拉玛依·统考三模)函数在区间上的所有零点之和为( )
A.B.
C.D.
11.(2022·陕西安康·统考一模)若函数有三个零点,则k的取值范围为( )
A.B.C.D.
12.(2023·河南·校联考模拟预测)已知函数若的图象上至少有两对点关于轴对称,则实数的取值范围是( )
A.B.C.D.
13.(2023·江西景德镇·统考模拟预测)若函数恰有两个零点,则实数的取值范围是( )
A.B.
C.D.
14.(2023·甘肃武威·统考一模)将函数的图象向右平移个单位长度,再将所得图象上所有点的横坐标变为原来的,纵坐标不变,得到函数的图象,若在上恰有2个零点,则的取值范围为( )
A.B.C.D.
15.(2022·安徽合肥·合肥市第五中学校考模拟预测)已知函数在内恰有3个最值点和4个零点,则实数的取值范围是( )
A.B.C.D.
16.(2020·福建三明·校联考模拟预测)下列区间中,函数一定存在零点的区间是( )
A.B.C.D.
17.(2020·山东日照·校联考模拟预测)函数的零点所在区间为( )
A.B.C.D.
18.(2019·甘肃平凉·静宁县第一中学校考一模)函数的零点所在区间为( )
A.B.C.D.
19.(2012·浙江衢州·统考一模)设函数,则在下面区间中函数不存在零点的是
A.B.C.D.
20.(2017·湖南·长郡中学校联考一模)已知表示不超过实数的最大整数,为取整函数,是函数的零点,则等于( )
A.1B.2C.3D.4
二、多选题
21.(2022·山东济南·山东省实验中学校考模拟预测)已知函数是定义在R上的偶函数,且当时,,那么函数在定义域内的零点个数可能是( )
A.2B.4C.6D.8
22.(2022·福建泉州·统考模拟预测)设函数,则下列判断正确的是( )
A.存在两个极值点
B.当时,存在两个零点
C.当时,存在一个零点
D.若有两个零点,则
23.(2022·江苏南通·统考模拟预测)已知分别是函数和的零点,则( )
A.B.
C.D.
24.(2022·河北石家庄·石家庄二中校考模拟预测)设函数,若关于的方程有四个实数解,且,则的值可能是( )
A.0B.1C.99D.100
25.(2023·全国·模拟预测)已知函数在上恰有三个零点,则( )
A.的最小值为B.在上只有一个极小值点
C.在上恰有两个极大值点D.在上单调递增
备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题08 函数图像的判断【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版: 这是一份备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题08 函数图像的判断【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版,共20页。试卷主要包含了考向解读,知识点汇总,题型专项训练,高考真题及模拟题精选,题型精练,巩固基础等内容,欢迎下载使用。
备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题11 函数的零点【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)解析版: 这是一份备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题11 函数的零点【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)解析版,共45页。试卷主要包含了考向解读,知识点汇总,函数零点个数判断的一般方法,高考真题及模拟题精选,题型精练,巩固基础等内容,欢迎下载使用。
备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题18 直线与方程【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版: 这是一份备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题18 直线与方程【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版,共14页。试卷主要包含了考向解读,知识点汇总,题型专项训练,高考真题及模拟题精选,题型精练,巩固基础等内容,欢迎下载使用。

备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题19 圆的方程【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版

备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题20 椭圆【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版
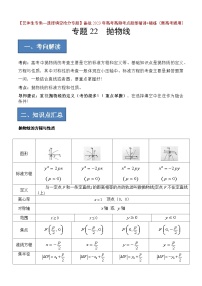
备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题22 抛物线【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版

备战2024年高考数学一轮复习艺体生高频考点专用复习讲义word版专题23 导数与切线【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练(新高考通用)原卷版








