江苏省南京市鼓楼区2023-2024学年八年级上学期期末数学试卷

这是一份江苏省南京市鼓楼区2023-2024学年八年级上学期期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
注意事项：
本试卷共6页．全卷满分100分．考试时间为100分钟．考生答题全部答在答题卡上，答在本试卷上无效．
一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
01．下列图案中，是轴对称图形的是
A B C D
02．在实数－ eq \f(1,7) eq\f(2,3)，eq \r(3,3)，0.eq \(\s\up1(.),6)，πeq\f(π,3)中，无理数有
A．1个 B．2个 C．3个 D．4个
03．若x2＝a (a＞0) ，则下列说法正确的是
A．a是x的平方根 B．x是a的平方根
C．x是a的算术平方根 D．a是x的算术平方根
04．若点P(m－1，m＋1)在第二象限，则m的值可以是
A．－2 B．－1 C．0 D．1
甲公司
一星期内送出的前240瓶牛奶，每瓶牛奶0.5元，此后，每多多送出一瓶则加上0.5元．
乙公司
底薪200元．此外，每送出一瓶牛奶将额外有0.4元．
05．两家牛奶销售公司招聘送奶员，下面的海报显示两家公司的周薪计算方式：
周薪/元
数量/瓶
A
C
数量/瓶
周薪/元
B
数量/瓶
周薪/元
D
数量/瓶
周薪/元
小明决定应聘当送奶员，下列表示两家公司的周薪计算方式正确的图是
0E
C
B
A
D
F
（第6题）
6．如图，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，
点A在ED上．若AE=1，AD=3，则BC的长为
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
07．64的平方根是 ▲ ，64的立方根是 ▲ ．
08．小亮称得一个罐头的质量为2.16 kg，若精确到0.1 kg，则这个罐头质量的近似值为 ▲ kg．
每年发电所得的利润
建造风力发电塔的成本
F = 400 000x – 3200 000
（第11题）
09．在△ABC中，AB＝AC，∠A＝70°，则∠B＝ ▲ °．
10．比－ eq \r(2)大且比 eq \r(3)小的整数是 ▲ （写出一个）．
11．电力公司想要估计某种风力发电塔的建造成本和所带来的利润，调查小组提出用如图的公式估计财务营收，其中 F （元）为财务营收，x （年）为时间．根据公式，至少需要 ▲ 年才能收回成本．
12．如图，∠A＝∠D＝90°，要使△ABC≌△DCB，需要添加的条件是 ▲ ．（写出一个）
（第12题）
A
B
C
D
E
B'
（第16题）
A
B
C
（第13题）
A
B
C
D
13．如图，一架2.5 m长的梯子AB，斜靠在竖直的墙AC上，这时梯子的底部B到墙底端C的距离为1.5 m，则梯子的顶端距地面为 ▲ m．
风寒效应是一种因刮风所引起的使体感温度较实际气温低的现象，科学家提出用风寒温度描述刮风时的体感温度，并通过大量实验找出了风寒温度和风速的关系．当气温为5 °Ｃ时，下表列出了风寒温度和风速的几组对应值，那么Ｔ与v的函数表达式可能是 ▲ ．
15．要使一次函数y＝－3x＋2的图象经过运动后过点（1，－7），则以下该函数图象的运动方式中，可行的是 ▲ ．（只填序号）
① 向下平移9个单位长度； ② 绕点（0，－1）旋转180°；
③ 沿着经过点（2，0）且平行于y轴的直线翻折．
16．如图，在△ABC中，∠ACB＝135°，AC＝eq \r(2)，BC＝ eq \f(5,3)，D，E分别是AB，BC边上的点．把△ABC沿直线DE折叠，若B落在AC边上的点B'处，则CE的取值范围是 ▲ ．
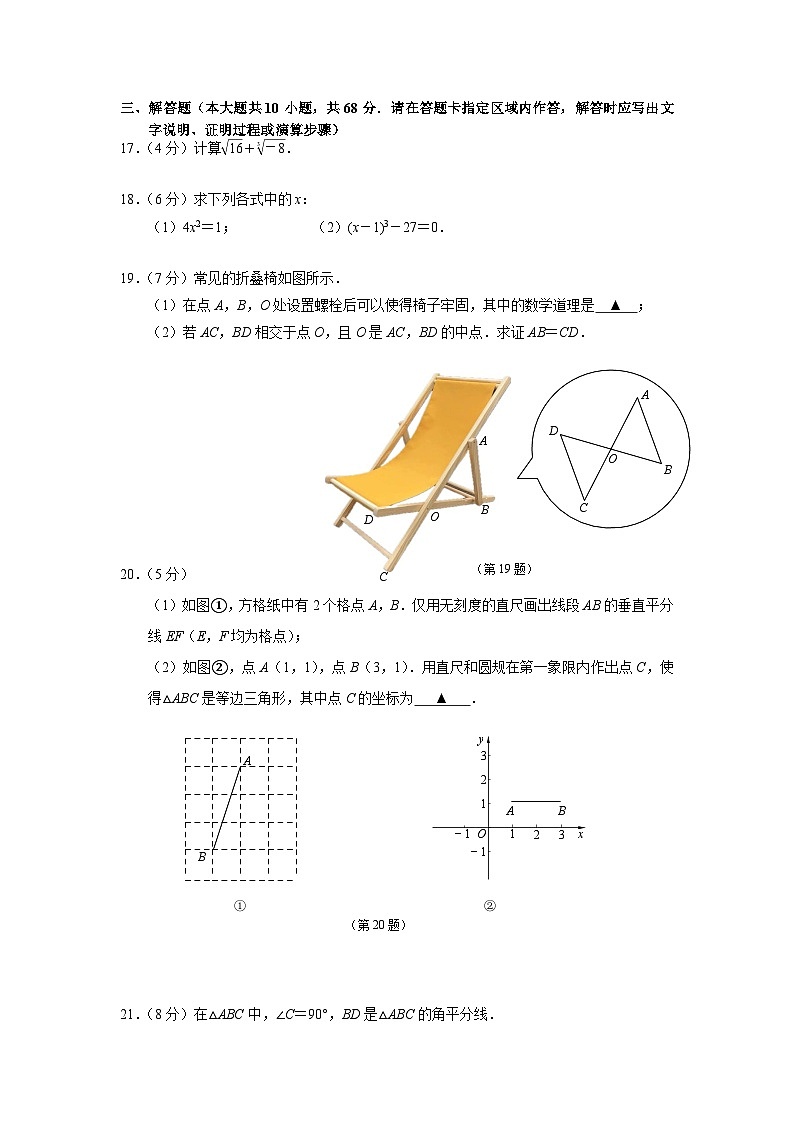
三、解答题（本大题共10小题，共68分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（4分）计算 eq \r(16)＋ eq \r(3,－8)．
18．（6分）求下列各式中的x：
（1）4x2＝1； （2）(x－1)3－27＝0．
19．（7分）常见的折叠椅如图所示．
（1）在点A，B，O处设置螺栓后可以使得椅子牢固，其中的数学道理是 ▲ ；
（2）若AC，BD相交于点O，且O是AC，BD的中点．求证AB＝CD．
A
B
O
D
C
A
B
O
D
C
（第19题）
20．（5分）
（1）如图①，方格纸中有2个格点A，B．仅用无刻度的直尺画出线段AB的垂直平分线EF（E，F均为格点）；
（2）如图②，点A（1，1），点B（3，1）．用直尺和圆规在第一象限内作出点C，使得△ABC是等边三角形，其中点C的坐标为 ▲ ．
（第20题）
A
B
①
②
y
－1
1
2
O
x
3
－1
1
2
3
A
B
21．（8分）在△ABC中，∠C＝90°，BD是△ABC的角平分线．
（1）如图①，若AC＝8，BC＝6，求CD的长；
（2）如图②，过点D作DG∥BC交AB于点G，求证：△GBD是等腰三角形．
A
B
C
D
= 1 \* GB3 ①
A
B
C
D
G
= 2 \* GB3 ②
（第21题）
22．（7分）数形结合是一种重要的数学思想方法，一般分为两种情形：借助于数学运算来阐明“形”的某些属性；借助于几何直观来阐明“数”的某种关系．
（1）从“数”的角度：证明“点A（－3，7），B（－1，3）和C（5，－9）在同一条直线上”；
（第22题）
（2）从“形”的角度：在方格纸中画出图形，并说明“eq \r(2)＋eq \r(5)＞eq \r(13)”．
23．（7分）如图，在△ABC中，AB＝AC，△ADC和△ABE分别是以AC，AB为腰的等腰直角三角形，BE与CD相交于点F．
B
C
D
E
F
A
（第23题）
（1）求证∠FBC＝∠FCB；
（2）连接AF，求证AF⊥BC．
24．（7分）在△ABC中， AB＝c，AC＝b，BC＝a．
（1）若∠C＝90°，则a，b，c满足的数量关系为 ▲ ；
（2）若△ABC为钝角三角形，a＝2，b＝1，直接写出c的取值范围；
（3）如图，若△ABC为锐角三角形，c为最长边．求证a2＋b2＞c2．
（第24题）
A
B
C
a
b
c
25．（8分）如图，在△ABC中，AB＝AC＝5，BC＝6．
（1）求△ABC各顶点的坐标；
y
x
O
A
B
C
（第25题）
（2）找一点P，使得△PAB，△PAC，△PBC均为等腰三角形，画出所有满足条件的点P（在图中用P1，P2，…表示），并直接写出点P的坐标．
y
x
O
A
B
C

26．（9分）如图①，一辆货车从南京出发匀速驶往上海，途经苏州，同时，一辆轿车从苏州出发匀速驶往南京，到达南京后停留1小时，然后原速返回苏州，两车同时到达目的地．设货车行驶x h时，货车与苏州的距离为y1 km，轿车与苏州的距离为y2 km，y1、y2与x的函数图象如图②所示．
（1）货车的速度是 ▲ km/h，轿车的速度是 ▲ km/h；
（2）通过计算，分别解释点G，H的实际意义；
（3）设轿车、货车的距离为s km，在图③中画出s与x的函数图象（标明必要的数据）．
南京
上海
①
苏州
②
O
x/h
210
5
3
y/km
A
D
E
H
F
C
B
G
S/km
200
100
250
150
50
1
2
3
4
5
O
③
x/h
（第26题）
八年级（上）期末试卷
数学参考答案及评分标准
说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．
一、选择题（本大题共6小题，每小题2分，共12分）
二、填空题（本大题共10小题，每小题2分，共20分）
三、解答题（本大题共10小题，共68分）
17．（4分）解：原式＝4－2 2分
＝2 4分
18．（6分）（1）解：x2＝ EQ \F(1, 4 )1分
x＝ EQ \F( 1 , 2 )或x＝－ EQ \F( 1 , 2 )；3分
（2）解：(x－1)3＝274分
x－1＝35分
x＝4．6分
19．（7分）（1）三角形的稳定性；2分
（2）证明：∵O是AC、BD的中点，
∴OA＝OC，OB＝OD．3分
在△AOB和△COD中，
eq \b\lc\{(\a\al(OA＝OC，,∠AOB＝∠COD，,OB＝OD．))
∴△AOB≌△COD（SSS）．6分
∴AB＝CD．7分
20．（5分）（1）如图①；2分
（2）作图正确，3分
（第20题）
B
①
②
E
F
A
x
1
2
3
4
1
2
3
4
B
C
y
O
A
（2，1＋ eq \r(3)）5分
21．（8分）（1）过点D作DE⊥AB，垂足为点E． 1分
∵BD平分∠ABC，
∴∠EBD＝∠CBD．
∵DE⊥AB，
∴∠DEB＝∠DEA＝90°．
A
B
C
D
E
∴∠DEB＝∠C．
在△BDC和△BDE中
eq \b\lc\{(\a\al(∠C＝∠BED，,∠CBD＝∠EBD，,BD＝BD．))
∴△BDC≌△BDE（AAS）．3分
∴CD＝ED， BC＝BE＝6．
在Rt△ABC中，∠C＝90°，AB＝ eq \r(BC2+AC2) ＝10．
（第21题①）
∴AE＝10－6＝4．
设CD＝x，则ED＝CD＝x，AD＝8－x．
A
B
C
D
G
（第21题 = 2 \* GB3 ②）
在Rt△ADE中，∠AED＝90°，
∴AE2＋ED2＝AD2．
∴42＋x2＝(8－x)2．
解得x＝3．即CD＝3．5分
（2）∵DG∥BC，
∴∠GDB＝∠CBD．6分
∵∠CBD＝∠GBD，
∴∠GDB＝∠GBD．7分
∴DG＝BG．即△GBD是等腰三角形．8分
22．（7分）（1）设AB所在直线的函数表达式为y＝kx＋b．
当x＝－3时，y＝7；当x＝－1时，y＝3．
则 eq \b\lc\{(\a\vs3\al(7＝－3k＋b，,3＝－k＋b．))解得 eq \b\lc\{(\a\vs3\al(k＝－2，,b＝1．))
∴AB所在直线的函数表达式为y＝－2x＋1．2分
A
B
C
（第22题）
当x＝5时，y＝－2×5＋1＝－9．3分
∴点C在AB所在的直线上．
即点A、B和C在同一条直线上．4分
如图，AB＝eq \r(2)，AC＝eq \r(5)，BC＝eq \r(13)，6分
根据“三角形两边之和大于第三边”，可得AB＋AC＞BC．
即eq \r(2)＋eq \r(5)＞eq \r(13)．7分
23．（7分）（1）证明：∵△ADC和△ABE分别是以AC、AB为腰的等腰直角三角形，
∴∠ABE＝∠ACD＝45°．1分
∵AB＝AC，
B
C
D
E
F
A
（第23题）
∴∠ABC＝∠ACB．2分
∴∠ABE－∠ABC＝∠ACD－∠ACB．
即∠FBC＝∠FCB．3分
（2）∵∠FBC＝∠FCB，
∴FB＝FC．4分
∴点F在BC的垂直平分线上．
∵AB＝AC，
∴点A在BC的垂直平分线上．6分
∴AF是BC的垂直平分线．
∴AF⊥BC．7分
（第24题）
A
B
C
a
b
c
D
24．（7分）（1）a2＋b 2＝c2；1分
（2）1＜c＜ eq \r(3)或 eq \r(5)＜c＜3； 3分
过点A作AD⊥BC，垂足为点D．
设CD＝x，则BD＝a－x．
∵AD⊥BC，
∴∠ADB＝∠ADC＝90°．
在Rt△ADC中，
则AD2＝AC2－CD2＝b2－x2．
同理：AD 2＝c2－(a－x)2．
（第25题）
P1
y
x
O
P3
P2
P4
P5
P6
A
B
C
∴b2－x2＝c2－(a－x)2．5分
∴a2＋b 2＝c2＋2ax．
∵2ax＞0，
∴a2＋b 2＞c2．7分
25．（8分）（1）A（0，4）、B（－3，0）、C（3，0）；
（写对1个或2个得1分，全部正确得2分）2分
（2）如图：P1（0，9）、P2（0，－1）、P3（0， eq \f(7,8)）、
P4（0，－4）、 P5（－ eq \f(117,25)， eq \f(144,25)）、P6（ eq \f(117,25)， eq \f(144,25)）
（写对1个坐标得1分，画图不扣分）8分
26．（9分）（1）70，105；2分
（2）设AB所在直线的函数表达式为y＝kx＋b．
则 eq \b\lc\{(\a\vs3\al(210＝b，,3k＋b＝0．))解得 eq \b\lc\{(\a\vs3\al(k＝－70，,b＝210．))∴ y＝－70x＋210（0≤x＜3）．
∵货车的速度是70 km/h，
∴BC所在直线的函数表达式为y＝70（x－3）＝70x－210（3≤x≤5）．
∵轿车的速度是105 km/h，
∴OD所在直线的函数表达式为y＝105x（0≤x≤2），
EF所在直线的函数表达式为y＝－105（x－5）＝－105x＋525（3≤x≤5）．
由 EQ \B\lc\{(\a\al(y＝－70x＋210，,y＝105x))得， EQ \B\lc\{(\a\al(x＝1.2，,y＝126)) ∴G（1.2，126）．3分
由 EQ \B\lc\{(\a\al(y＝70x－210，,y＝－105x＋525))得， EQ \B\lc\{(\a\al(x＝4.2，,y＝84)) ∴H（4.2，84）．4分
∴点G的实际意义为：轿车与货车出发1.2 h时，在距苏州126 km的地方相遇．5分
点H的实际意义为：轿车与货车出发4.2 h时，都距苏州84 km．6分
（3）如图：9分
S/km
200
100
250
150
50
2
3
5
O
（第26题）
③
x/h
140
210
1.2
A．eq \r(5)
B．eq \r(6)
C．2.5
D．eq \r(8)
风速v（km/h）
0
10
20
30
40
风寒温度Ｔ（°Ｃ）
5
3
1
－1
－3
题号
1
2
3
4
5
6
答案
D
B
B
C
A
A
07．±8，4
08．2.2
09．55
10．0 （答案不唯一）
11．8
12．AB＝DC（答案不唯一）
13．2
14．T＝－0.2v＋5
15．②③
16． eq \f(7,48)≤CE≤ eq \f(5,6)