
2023-2024学年江苏省扬州市高邮市汪曾祺学校数学九年级第一学期期末达标检测试题含答案
展开学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)
1.对于反比例函数,如果当≤≤时有最大值,则当≥8时,有( )
A.最大值B.最小值C.最大值=D.最小值=
2.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若BO=6cm,OC=8cm 则BE+CG的长等于( )
A.13B.12C.11D.10
3.在平面直角坐标系中,抛物线与轴交于点,与轴交于点,则的面积是 ( )
A.6B.10C.12D.15
4.若我们把十位上的数字比个位和百位上数字都小的三位数,称为“”或,如,,那么从2,3,4这三个数字组成的无重复数字的三位数中任意抽取一个数,则该数是“”数的槪率为( )
A.B.C.D.
5.下列图形中是中心对称图形又是轴对称图形的是( )
A.B.C.D.
6.已知关于的二次函数的图象在轴上方,并且关于的分式方程有整数解,则同时满足两个条件的整数值个数有( ).
A.2个B.3个C.4个D.5个
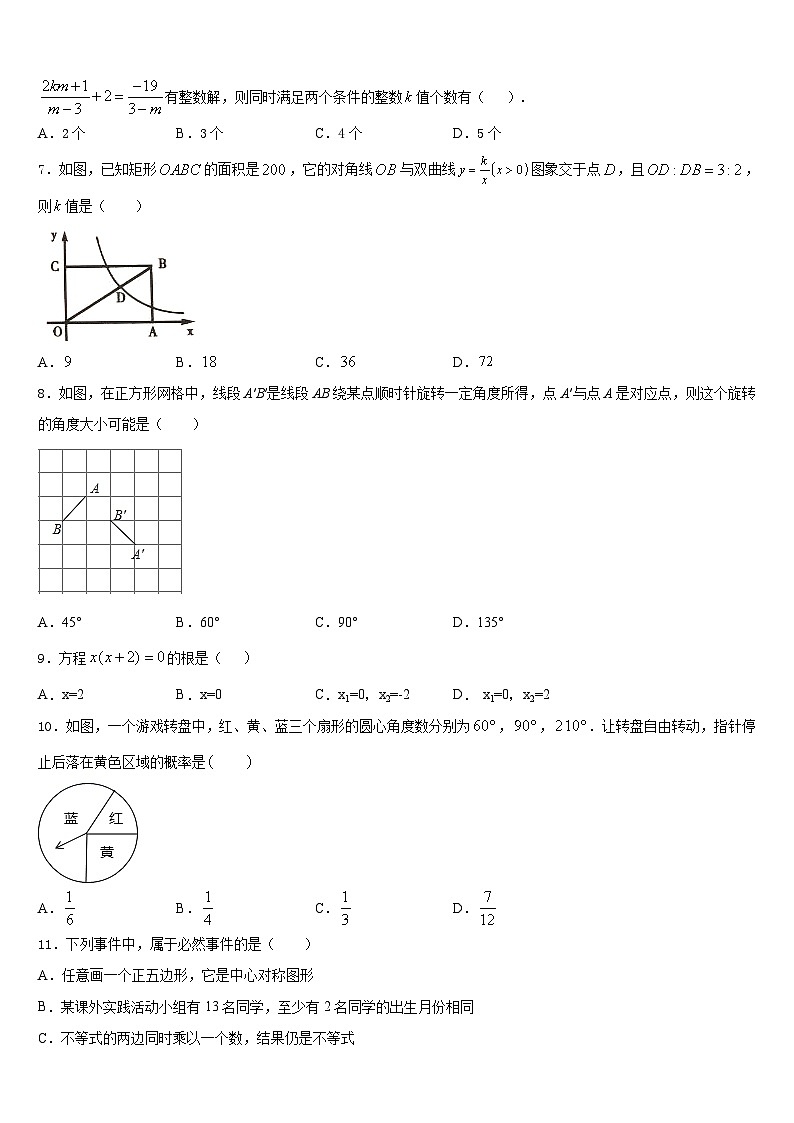
7.如图,已知矩形的面积是,它的对角线与双曲线图象交于点,且,则值是( )
A.B.C.D.
8.如图,在正方形网格中,线段A′B′是线段AB绕某点顺时针旋转一定角度所得,点A′与点A是对应点,则这个旋转的角度大小可能是( )
A.45°B.60°C.90°D.135°
9.方程的根是( )
A.x=2B.x=0C.x1=0,x2=-2D. x1=0,x2=2
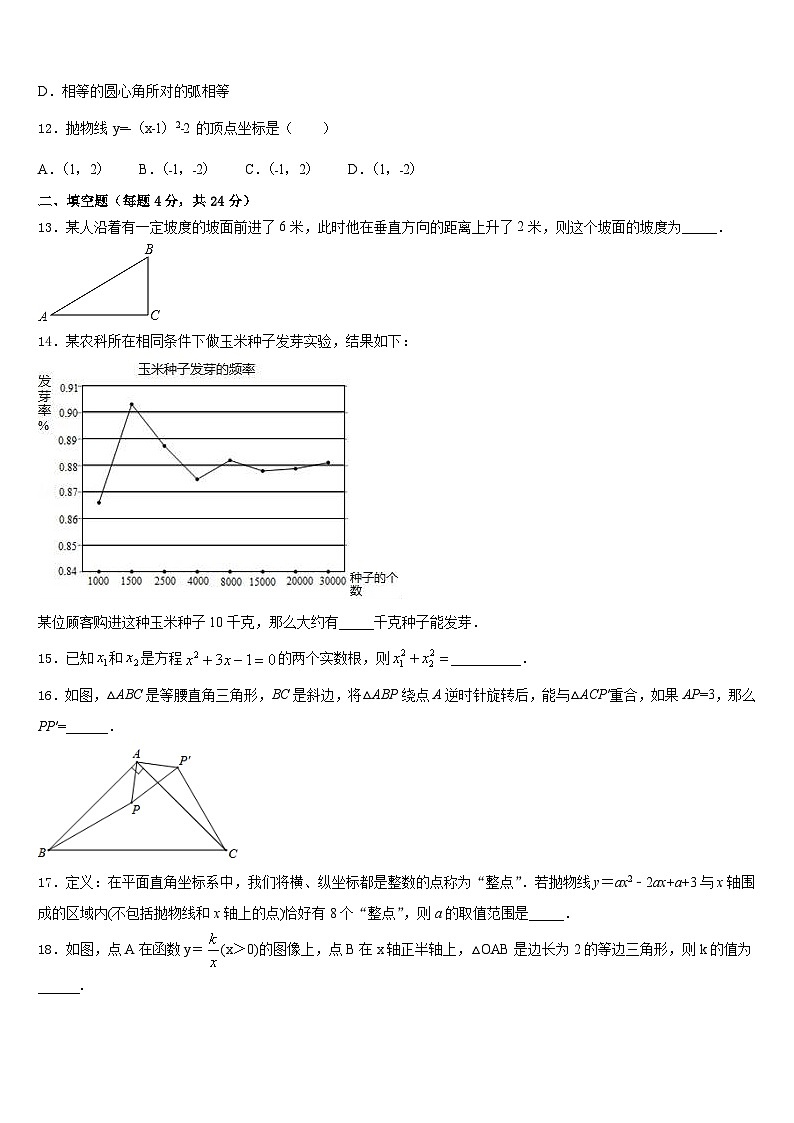
10.如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为,,.让转盘自由转动,指针停止后落在黄色区域的概率是
A.B.C.D.
11.下列事件中,属于必然事件的是( )
A.任意画一个正五边形,它是中心对称图形
B.某课外实践活动小组有13名同学,至少有2名同学的出生月份相同
C.不等式的两边同时乘以一个数,结果仍是不等式
D.相等的圆心角所对的弧相等
12.抛物线 y=﹣(x﹣1)2﹣2 的顶点坐标是( )
A.(1,2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
二、填空题(每题4分,共24分)
13.某人沿着有一定坡度的坡面前进了6米,此时他在垂直方向的距离上升了2米,则这个坡面的坡度为_____.
14.某农科所在相同条件下做玉米种子发芽实验,结果如下:
某位顾客购进这种玉米种子10千克,那么大约有_____千克种子能发芽.
15.已知和是方程的两个实数根,则__________.
16.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′=______.
17.定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是_____.
18.如图,点A在函数y=(x>0)的图像上,点B在x轴正半轴上,△OAB是边长为2的等边三角形,则k的值为______.
三、解答题(共78分)
19.(8分)如图,是的直径,点,是上两点,且,连接,,过点作交延长线于点,垂足为.
(1)求证:是的切线;
(2)若,求的半径.
20.(8分)解方程:(x+2)(x-5)=1.
21.(8分)如图,在中,,点P为内一点,连接PA,PB,PC,求PA+PB+PC的最小值,小华的解题思路,以点A为旋转中心,将顺时针旋转得到,那么就将求PA+PB+PC的值转化为求PM+MN+PC的值,连接CN,当点P,M落在CN上时,此题可解.
(1)请判断的形状,并说明理由;
(2)请你参考小华的解题思路,证明PA+PB+PC=PM+MN+PC;
(3)当,求PA+PB+PC的最小值.
22.(10分)游乐园新建的一种新型水上滑道如图,其中线段表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道可以看作反比例函数图象的一部分,滑道可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数的顶点,且点B到水面的距离,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离,与点B的水平距离.
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道的水平距离;
(3)若小明站在平台上相距y轴的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道上(包括B、D两点),直接写出p的取值范围.
23.(10分)如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
24.(10分)如图,在中,,,夹边的长为6,求的面积.
25.(12分)已知关于x的方程.
求证:不论m为何值,方程总有实数根;
当m为何整数时,方程有两个不相等的正整数根?
26.(12分)安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量(千克)与每千克降价(元)之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
参考答案
一、选择题(每题4分,共48分)
1、D
2、D
3、A
4、C
5、A
6、B
7、D
8、C
9、C
10、B
11、B
12、D
二、填空题(每题4分,共24分)
13、
14、1.1
15、1
16、3
17、
18、
三、解答题(共78分)
19、(1)见解析;(2)圆O 的半径为1
20、x1=7,x2=-2
21、(1)等边三角形,见解析;(2)见解析;(3)
22、(1),;(2)7m;(3).
23、(1);(2)π﹣.
24、△ABC的面积是.
25、(1)见解析;(2).
26、(1);(2)商贸公司要想获利2090元,则这种干果每千克应降价9元.
2023-2024学年江苏省扬州市高邮市汪曾祺学校九上数学期末复习检测试题含答案: 这是一份2023-2024学年江苏省扬州市高邮市汪曾祺学校九上数学期末复习检测试题含答案,共9页。试卷主要包含了如图,点A,如图所示的几何体的左视图为等内容,欢迎下载使用。
江苏省扬州市高邮汪曾祺学校2022—2023学年上学期七年级入学检测数学试题: 这是一份江苏省扬州市高邮汪曾祺学校2022—2023学年上学期七年级入学检测数学试题,共12页。
2023-2024学年江苏省扬州市高邮市汪曾祺学校数学八上期末达标检测模拟试题含答案: 这是一份2023-2024学年江苏省扬州市高邮市汪曾祺学校数学八上期末达标检测模拟试题含答案,共8页。试卷主要包含了下列计算正确的是等内容,欢迎下载使用。












