

还剩6页未读,
继续阅读
2023-2024学年江苏省南京市东山外国语学校九上数学期末经典模拟试题含答案
展开
这是一份2023-2024学年江苏省南京市东山外国语学校九上数学期末经典模拟试题含答案,共9页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)
1. 如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
A.20°B.30°C.40°D.70°
2.如图,在中,,将绕点旋转到'的位置,使得,则的大小为( )
A.B.C.D.
3.在开展“爱心捐助”的活动中,某团支部8名团员捐款的数额(单位:元)分别为3,5,6,5,6,5,5,10,这组数据的中位数是( )
A.3元B.5元C.5.5元D.6元
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠CB.∠APB=∠ABC
C.D.
5.用配方法解方程,变形后的结果正确的是( )
A.B.C.D.
6.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到颜色相同的球的概率为( )
A.B.C.D.
7.电影《流浪地球》一上映就获得追捧,第一天票房收入约8亿元,第三天票房收入达到了11.52亿元,设第一天到第三天票房收入平均每天增长的百分率为x,则可列方程( )
A.8(1+x)=11.52B.8(1+2x)=11.52
C.8(1+x)=11.52D.8(1﹣x)=11.52
8.如图,正方形的顶点分别在轴和轴上,与双曲线恰好交于的中点. 若,则的值为( )
A.6B.8C.10D.12
9.如图是由4个大小相同的立方块搭成的几何体,这个几何体的主视图是( )
A.B.C.D.
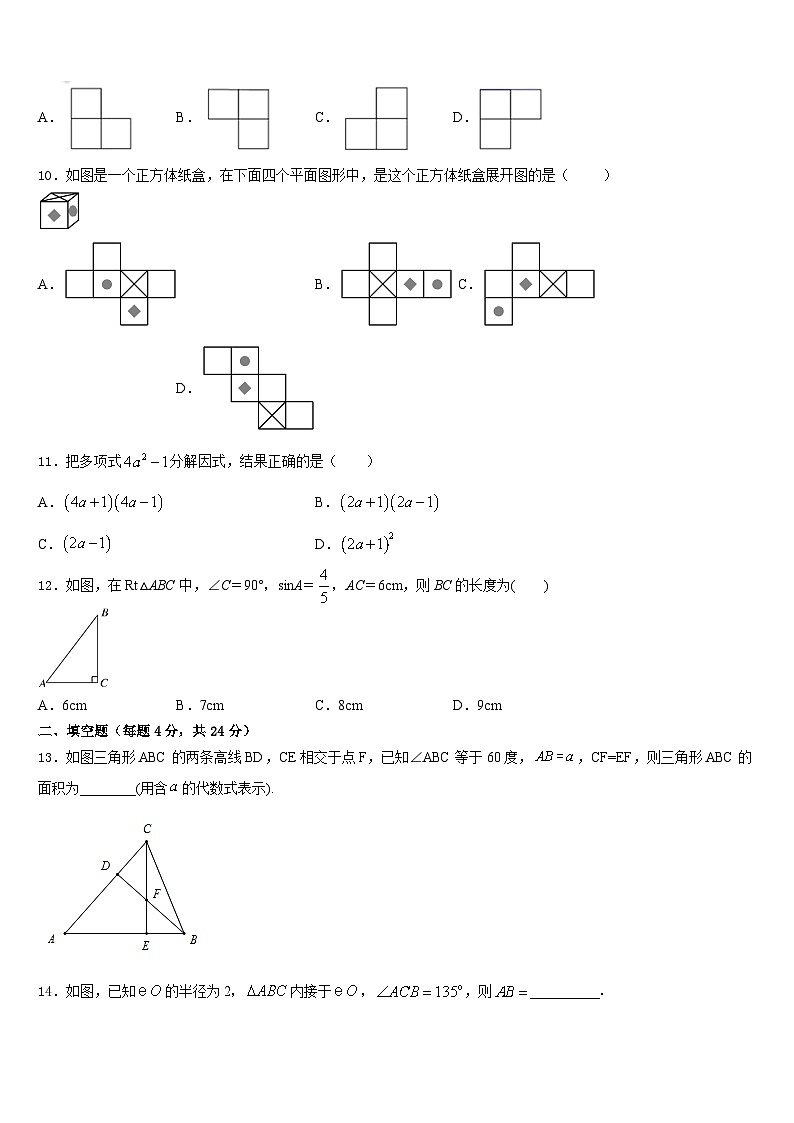
10.如图是一个正方体纸盒,在下面四个平面图形中,是这个正方体纸盒展开图的是( )
A.B.C.D.
11.把多项式分解因式,结果正确的是( )
A.B.
C.D.
12.如图,在Rt△ABC中,∠C=90°,sinA=,AC=6cm,则BC的长度为( )
A.6cmB.7cmC.8cmD.9cm
二、填空题(每题4分,共24分)
13.如图三角形ABC的两条高线BD,CE相交于点F,已知∠ABC等于60度,,CF=EF,则三角形ABC的面积为________(用含的代数式表示).
14.如图,已知的半径为2,内接于,,则__________.
15.如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
16.已知反比例函数,在其位于第三像限内的图像上有一点M,从M点向y轴引垂线与y轴交于点N,连接M与坐标原点O,则ΔMNO面积是_____.
17.若圆锥的底面圆半径为,圆锥的母线长为,则圆锥的侧面积为______.
18.如图,已知二次函数顶点的纵坐标为,平行于轴的直线交此抛物线,两点,且,则点到直线的距离为__________
三、解答题(共78分)
19.(8分)如图1,抛物线y=ax2+bx+c的顶点(0,5),且过点(﹣3,),先求抛物线的解析式,再解决下列问题:
(应用)问题1,如图2,线段AB=d(定值),将其弯折成互相垂直的两段AC、CB后,设A、B两点的距离为x,由A、B、C三点组成图形面积为S,且S与x的函数关系如图所示(抛物线y=ax2+bx+c上MN之间的部分,M在x轴上):
(1)填空:线段AB的长度d= ;弯折后A、B两点的距离x的取值范围是 ;若S=3,则是否存在点C,将AB分成两段(填“能”或“不能”) ;若面积S=1.5时,点C将线段AB分成两段的长分别是 ;
(2)填空:在如图1中,以原点O为圆心,A、B两点的距离x为半径的⊙O;画出点C分AB所得两段AC与CB的函数图象(线段);设圆心O到该函数图象的距离为h,则h= ,该函数图象与⊙O的位置关系是 .
(提升)问题2,一个直角三角形斜边长为c(定值),设其面积为S,周长为x,证明S是x的二次函数,求该函数关系式,并求x的取值范围和相应S的取值范围.
20.(8分)某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不得超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接待第四个月的进馆人次,并说明理由.
21.(8分)如图,在四边形中,将绕点顺时针旋转一定角度后,点的对应点恰好与点重合,得到.
(1)求证:;
(2)若,试求四边形的对角线的长.
22.(10分)如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
(1)用含t的代数式分别表示点E和点F的坐标;
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值;
(3)当t=2时,求O′点在坐标.
23.(10分)如图,抛物线与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=1.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
注:二次函数(≠0)的对称轴是直线=.
24.(10分)如图,已知是的直径,点在上,过点的直线与的延长线交于点,.
求证:是的切线;
求证:;
点是弧的中点,交于点,若,求的值.
25.(12分)如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.
(1)当a=2,y=3时,求x的值;
(2)当x为何值时,y的值最小?最小值是多少?
26.(12分)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
参考答案
一、选择题(每题4分,共48分)
1、A
2、B
3、B
4、D
5、D
6、C
7、C
8、D
9、A
10、C
11、B
12、C
二、填空题(每题4分,共24分)
13、
14、
15、②③
16、3
17、
18、1
三、解答题(共78分)
19、抛物线的解析式为:y=﹣x2+5;(2)20<x<2,不能,+和﹣;(2),相离或相切或相交;(3)相应S的取值范围为S>c2.
20、(1)进馆人次的月平均增长率为50%;(2)校图书馆能接纳第四个月的进馆人次.理由见解析.
21、(1)见解析;(2).
22、(1)E(3t,0),F(12,10﹣2t);(2)t=;(3)O'(,)
23、(2)(2)P(,)
24、(1)详见解析;(2)详见解析;(3)1.
25、(1)x=;(1)当x=a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为a1.
26、(1)证明见解析;(2)BM=MC.理由见解析.
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)
1. 如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
A.20°B.30°C.40°D.70°
2.如图,在中,,将绕点旋转到'的位置,使得,则的大小为( )
A.B.C.D.
3.在开展“爱心捐助”的活动中,某团支部8名团员捐款的数额(单位:元)分别为3,5,6,5,6,5,5,10,这组数据的中位数是( )
A.3元B.5元C.5.5元D.6元
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠CB.∠APB=∠ABC
C.D.
5.用配方法解方程,变形后的结果正确的是( )
A.B.C.D.
6.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到颜色相同的球的概率为( )
A.B.C.D.
7.电影《流浪地球》一上映就获得追捧,第一天票房收入约8亿元,第三天票房收入达到了11.52亿元,设第一天到第三天票房收入平均每天增长的百分率为x,则可列方程( )
A.8(1+x)=11.52B.8(1+2x)=11.52
C.8(1+x)=11.52D.8(1﹣x)=11.52
8.如图,正方形的顶点分别在轴和轴上,与双曲线恰好交于的中点. 若,则的值为( )
A.6B.8C.10D.12
9.如图是由4个大小相同的立方块搭成的几何体,这个几何体的主视图是( )
A.B.C.D.
10.如图是一个正方体纸盒,在下面四个平面图形中,是这个正方体纸盒展开图的是( )
A.B.C.D.
11.把多项式分解因式,结果正确的是( )
A.B.
C.D.
12.如图,在Rt△ABC中,∠C=90°,sinA=,AC=6cm,则BC的长度为( )
A.6cmB.7cmC.8cmD.9cm
二、填空题(每题4分,共24分)
13.如图三角形ABC的两条高线BD,CE相交于点F,已知∠ABC等于60度,,CF=EF,则三角形ABC的面积为________(用含的代数式表示).
14.如图,已知的半径为2,内接于,,则__________.
15.如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
16.已知反比例函数,在其位于第三像限内的图像上有一点M,从M点向y轴引垂线与y轴交于点N,连接M与坐标原点O,则ΔMNO面积是_____.
17.若圆锥的底面圆半径为,圆锥的母线长为,则圆锥的侧面积为______.
18.如图,已知二次函数顶点的纵坐标为,平行于轴的直线交此抛物线,两点,且,则点到直线的距离为__________
三、解答题(共78分)
19.(8分)如图1,抛物线y=ax2+bx+c的顶点(0,5),且过点(﹣3,),先求抛物线的解析式,再解决下列问题:
(应用)问题1,如图2,线段AB=d(定值),将其弯折成互相垂直的两段AC、CB后,设A、B两点的距离为x,由A、B、C三点组成图形面积为S,且S与x的函数关系如图所示(抛物线y=ax2+bx+c上MN之间的部分,M在x轴上):
(1)填空:线段AB的长度d= ;弯折后A、B两点的距离x的取值范围是 ;若S=3,则是否存在点C,将AB分成两段(填“能”或“不能”) ;若面积S=1.5时,点C将线段AB分成两段的长分别是 ;
(2)填空:在如图1中,以原点O为圆心,A、B两点的距离x为半径的⊙O;画出点C分AB所得两段AC与CB的函数图象(线段);设圆心O到该函数图象的距离为h,则h= ,该函数图象与⊙O的位置关系是 .
(提升)问题2,一个直角三角形斜边长为c(定值),设其面积为S,周长为x,证明S是x的二次函数,求该函数关系式,并求x的取值范围和相应S的取值范围.
20.(8分)某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不得超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接待第四个月的进馆人次,并说明理由.
21.(8分)如图,在四边形中,将绕点顺时针旋转一定角度后,点的对应点恰好与点重合,得到.
(1)求证:;
(2)若,试求四边形的对角线的长.
22.(10分)如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
(1)用含t的代数式分别表示点E和点F的坐标;
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值;
(3)当t=2时,求O′点在坐标.
23.(10分)如图,抛物线与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=1.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
注:二次函数(≠0)的对称轴是直线=.
24.(10分)如图,已知是的直径,点在上,过点的直线与的延长线交于点,.
求证:是的切线;
求证:;
点是弧的中点,交于点,若,求的值.
25.(12分)如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.
(1)当a=2,y=3时,求x的值;
(2)当x为何值时,y的值最小?最小值是多少?
26.(12分)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
参考答案
一、选择题(每题4分,共48分)
1、A
2、B
3、B
4、D
5、D
6、C
7、C
8、D
9、A
10、C
11、B
12、C
二、填空题(每题4分,共24分)
13、
14、
15、②③
16、3
17、
18、1
三、解答题(共78分)
19、抛物线的解析式为:y=﹣x2+5;(2)20<x<2,不能,+和﹣;(2),相离或相切或相交;(3)相应S的取值范围为S>c2.
20、(1)进馆人次的月平均增长率为50%;(2)校图书馆能接纳第四个月的进馆人次.理由见解析.
21、(1)见解析;(2).
22、(1)E(3t,0),F(12,10﹣2t);(2)t=;(3)O'(,)
23、(2)(2)P(,)
24、(1)详见解析;(2)详见解析;(3)1.
25、(1)x=;(1)当x=a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为a1.
26、(1)证明见解析;(2)BM=MC.理由见解析.












