2023-2024学年四川省南部县数学九年级第一学期期末学业质量监测模拟试题含答案

这是一份2023-2024学年四川省南部县数学九年级第一学期期末学业质量监测模拟试题含答案，共8页。试卷主要包含了一元二次方程的解是，如图，在中，，则的长度为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题（每题4分，共48分）
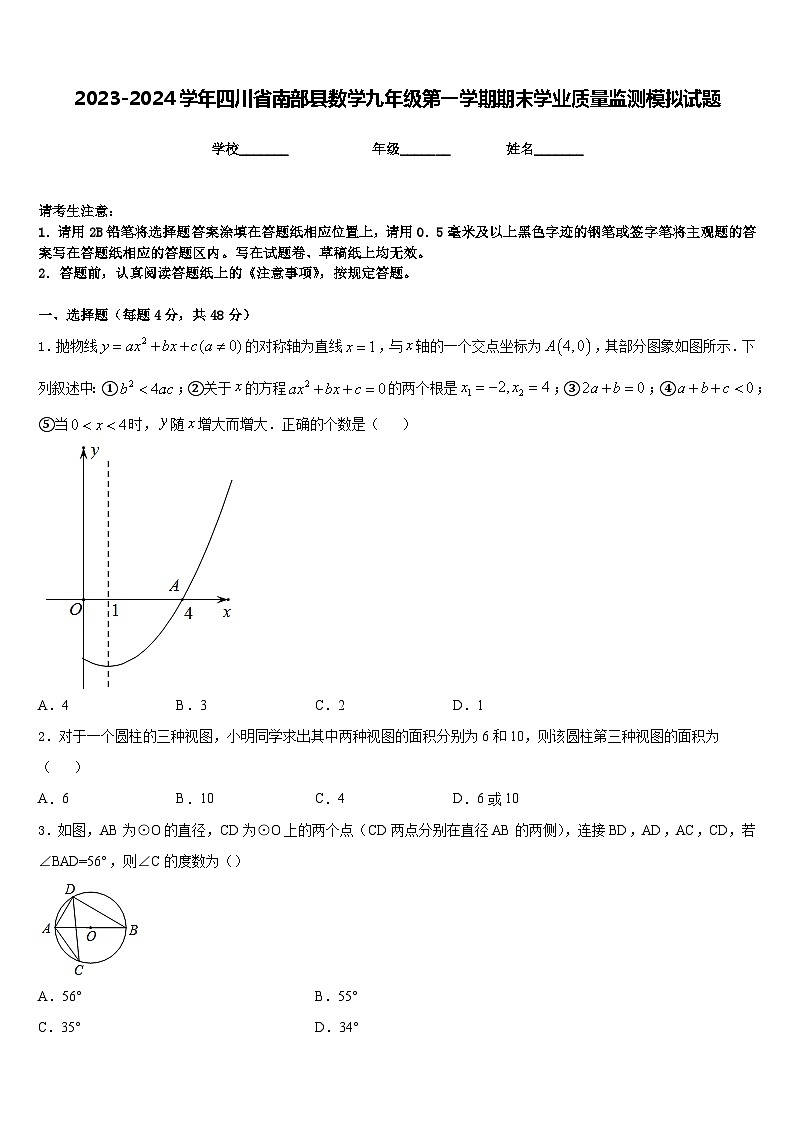
1．抛物线的对称轴为直线，与轴的一个交点坐标为，其部分图象如图所示．下列叙述中：①；②关于的方程的两个根是；③；④；⑤当时，随增大而增大．正确的个数是（ ）
A．4B．3C．2D．1
2．对于一个圆柱的三种视图，小明同学求出其中两种视图的面积分别为6和10，则该圆柱第三种视图的面积为（ ）
A．6B．10C．4D．6或10
3．如图，AB为⊙O的直径，CD为⊙O上的两个点（CD两点分别在直径AB的两侧），连接BD，AD，AC，CD，若∠BAD=56°，则∠C的度数为（）
A．56°B．55°
C．35°D．34°
4．一元二次方程的解是（ ）
A．x1＝2，x2＝-2B．x＝-2C．x＝2D．x1＝2，x2＝0
5．如图，传送带和地面成一斜坡，它把物体从地面送到离地面5米高的地方，物体所经过路程是13米，那么斜坡的坡度为（ ）
A．1：2.6B．1:C．1：2.4D．1:
6．如图，在中，，则的长度为
A．1B．C．D．
7．某班有40人，一次体能测试后，老师对测试成绩进行了统计．由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分，方差s2＝1．后来小亮进行了补测，成绩为90分，关于该班40人的测试成绩，下列说法正确的是（ ）
A．平均分不变，方差变大B．平均分不变，方差变小
C．平均分和方差都不变D．平均分和方差都改变
8．若抛物线y＝kx2﹣2x﹣1与x轴有两个不同的交点，则k的取值范围为( )
A．k＞﹣1B．k≥﹣1C．k＞﹣1且k≠0D．k≥﹣1且k≠0
9．在同一平面上，外有一定点到圆上的距离最长为10，最短为2，则的半径是（ ）
A．5B．3C．6D．4
10．如图，直线AC,DF被三条平行线所截，若 DE:EF=1:2，AB=2，则AC的值为（ ）
A．6B．4C．3D．
11．关于x的一元二次方程ax2﹣4x+1＝0有实数根，则整数a的最大值是（ ）
A．1B．﹣4C．3D．4
12．如图，抛物线的对称轴为，且过点，有下列结论：①＞0；②＞0；③；④＞0.其中正确的结论是（ ）
A．①③B．①④C．①②D．②④
二、填空题（每题4分，共24分）
13．计算：_______．
14．如图，的半径长为，与相切于点，交半径的延长线于点，长为，，垂足为，则图中阴影部分的面积为_______．
15．比较sin30°、sin45°的大小，并用“＜”连接为_____．
16．如图，是⊙的直径，，点、在⊙上，、的延长线交于点，且，，有以下结论：①；②劣弧的长为；③点为的中点；④平分，以上结论一定正确的是______．
17．已知抛物线的对称轴是直线，其部分图象如图所示，下列说法中：①；②；③；④当时，，正确的是_____（填写序号）．
18．如图，在中，，，点在上，且，则______．______．
三、解答题（共78分）
19．（8分）某商场销售一批名牌衬衫，平均每天可售出10件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出1件，若商场平均每天要盈利600元，每件衬衫应降价多少元？
20．（8分）如图，在矩形ABCD中，AB＝6，AD＝3，点E是边CD的中点，点P，Q分别是射线DC与射线EB上的动点，连结PQ，AP，BP，设DP＝t，EQ＝t．
（1）当点P在线段DE上（不包括端点）时．
①求证：AP＝PQ；②当AP平分∠DPB时，求△PBQ的面积．
（2）在点P，Q的运动过程中，是否存在这样的t，使得△PBQ为等腰三角形？若存在，请求出t的值；若不存在，试说明理由．
21．（8分）如图所示，以的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线.如果不考虑空气阻力，球的飞行高度（单位：）与飞行时间（单位：）之间具有关系式.解答以下问题：
（1）球的飞行高度能否达到?如能，需要飞行多少时间？
（2）球飞行到最高点时的高度是多少？
22．（10分）（1）计算：；
（2）解方程：．
23．（10分）国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
a．国家创新指数得分的频数分布直方图（数据分成7组：
30≤x＜40，40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）；
b．国家创新指数得分在60≤x＜70这一组的是：61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c．40个国家的人均国内生产总值和国家创新指数得分情况统计图：
d．中国的国家创新指数得分为69.5.
（以上数据来源于《国家创新指数报告（2018）》）
根据以上信息，回答下列问题：
（1）中国的国家创新指数得分排名世界第______；
（2）在40个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在内的少数几个国家所对应的点位于虚线的上方．请在图中用“”圈出代表中国的点；
（3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为______万美元；（结果保留一位小数）
（4）下列推断合理的是______．
①相比于点A，B所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加快建设创新型国家”的战略任务，进一步提高国家综合创新能力；
②相比于点B，C所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值．
24．（10分）已知关于的方程，其中是常数．请用配方法解这个一元二次方程．
25．（12分）如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点，直线经过，两点，抛物线的顶点为，对称轴与轴交于点．
（1）求此抛物线的解析式；
（2）求的面积；
（3）在抛物线上是否存在一点，使它到轴的距离为4，若存在，请求出点的坐标，若不存在，则说明理由．
26．（12分）如图，、交于点，，且平分．
（1）求证：；
（2）若，，，求的长．
参考答案
一、选择题（每题4分，共48分）
1、B
2、D
3、D
4、A
5、C
6、C
7、B
8、C
9、D
10、A
11、D
12、C
二、填空题（每题4分，共24分）
13、
14、
15、＜．
16、①②③
17、①③④．
18、
三、解答题（共78分）
19、平均每天要盈利600元，每件衬衫应降价20元
20、（1）①见解析；②S△PBQ＝18﹣9；（2）存在，满足条件的t的值为6﹣1或1或6+1．
21、（1）能，1或3；（2）20m
22、（1）；（2），
23、（1）17；（2）如图所示，见解析；（3）2.8；（4）①②.
24、详见解析.
25、（1）y＝﹣x2+x+2；（2）；（3）存在一点P或，使它到x轴的距离为1
26、（1）见解析；（2）