安徽界首地区2023-2024学年数学九年级第一学期期末学业质量监测模拟试题含答案

这是一份安徽界首地区2023-2024学年数学九年级第一学期期末学业质量监测模拟试题含答案，共9页。试卷主要包含了考生必须保证答题卡的整洁，点P1，方程等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．如图，在正方形 ABCD 中，E是BC的中点，F是CD上一点，AE⊥EF．有下列结论：
①∠BAE＝30°；
②射线FE是∠AFC的角平分线；
③CF＝CD；
④AF＝AB＋CF．
其中正确结论的个数为（ ）
A．1 个B．2 个C．3 个D．4 个
2．如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC的度数是（ ）
A．35°B．55°C．65°D．70°
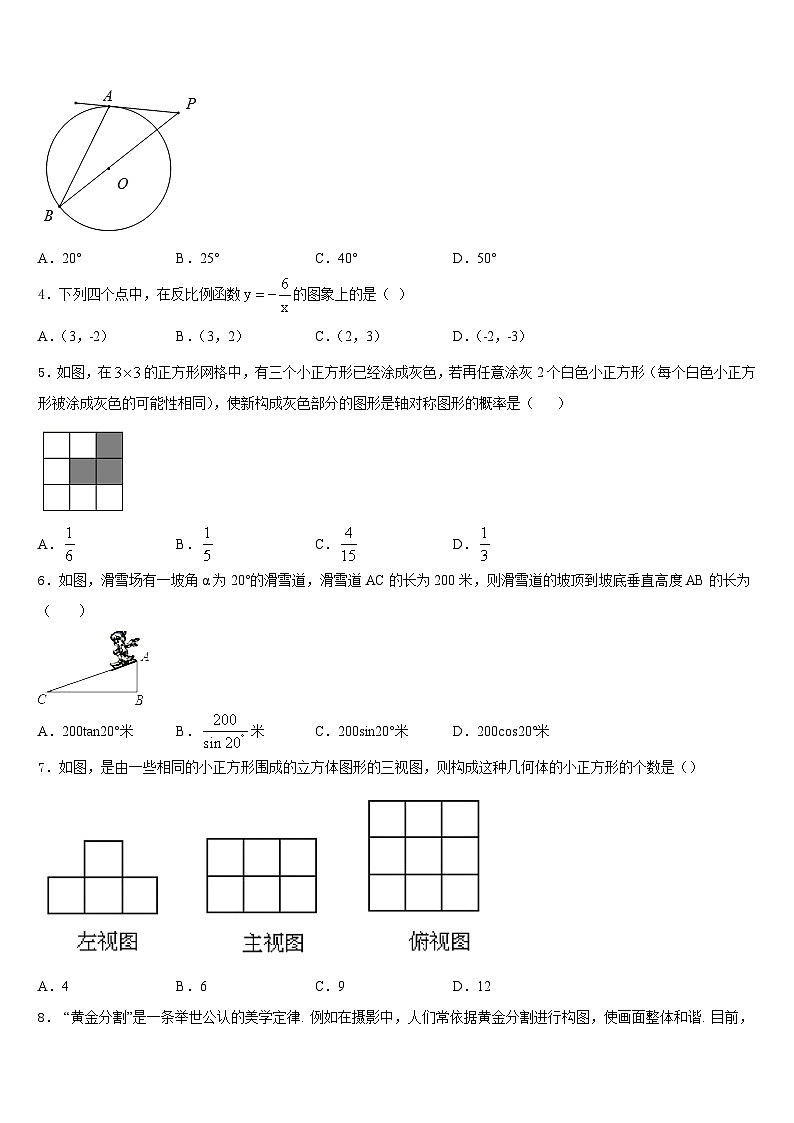
3．如图，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B，若∠P=40°，则∠B的度数为 （ ）
A．20°B．25°C．40°D．50°
4．下列四个点中，在反比例函数的图象上的是（ ）
A．（3，﹣2）B．（3，2）C．（2，3）D．（﹣2，﹣3）
5．如图，在的正方形网格中，有三个小正方形已经涂成灰色，若再任意涂灰2个白色小正方形（每个白色小正方形被涂成灰色的可能性相同），使新构成灰色部分的图形是轴对称图形的概率是（ ）
A．B．C．D．
6．如图，滑雪场有一坡角α为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底垂直高度AB的长为（ ）
A．200tan20°米B．米C．200sin20°米D．200cs20°米
7．如图，是由一些相同的小正方形围成的立方体图形的三视图，则构成这种几何体的小正方形的个数是（）
A．4B．6C．9D．12
8． “黄金分割”是一条举世公认的美学定律. 例如在摄影中，人们常依据黄金分割进行构图，使画面整体和谐. 目前，照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗，按照黄金分割的原则，应该使小狗置于画面中的位置（ ）
A．①B．②C．③D．④
9．点P1（﹣1，），P2（3，），P3（5，）均在二次函数的图象上，则，，的大小关系是（ ）
A．B．C．D．
10．方程（m﹣2）x2+mx﹣1＝0是关于x的一元二次方程，则m的值为（ ）
A．任何实数．B．m≠0C．m≠2D．m≠﹣2
11．如图，AB为⊙O的直径，C、D是⊙O上的两点，∠CDB＝25°，过点C作⊙O的切线交AB的延长线于点E，则∠E的度数为（ ）
A．40°B．50°C．55°D．60°
12．如图，在△ABC中，点D，E分别在AB，AC上，DE∥BC，且DE将△ABC分成面积相等的两部分，那么的值为（ ）
A．﹣1B．+1C．1D．
二、填空题（每题4分，共24分）
13．如图，抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A（-2,4），B（1,1），则不等式ax2＞bx+c的解集是_________.
14．如图，在平面直角坐标系中，点在抛物线上运动，过点作轴于点，以为对角线作矩形连结则对角线的最小值为 ．
15．若是方程的一个根，则式子的值为__________．
16．二次函数的最大值是__________．
17．一艘观光游船从港口以北偏东的方向出港观光，航行海里至处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东方向，马上以海里每小时的速度前往救援，海警船到达事故船处所需的时间大约为________小时（用根号表示）．
18．我市博览馆有A，B，C三个入口和D，E两个出口，小明入馆游览，他从A口进E口出的概率是____．
三、解答题（共78分）
19．（8分）在平面直角坐标系xOy中，已知抛物线G：y＝ax2﹣2ax+4（a≠0）．
（1）当a＝1时，
①抛物线G的对称轴为x＝ ；
②若在抛物线G上有两点（2，y1），（m，y2），且y2＞y1，则m的取值范围是 ；
（2）抛物线G的对称轴与x轴交于点M，点M与点A关于y轴对称，将点M向右平移3个单位得到点B，若抛物线G与线段AB恰有一个公共点，结合图象，求a的取值范围．
20．（8分）在平面直角坐标系中，四边形是矩形，点，点，点．以点为中心，顺时针旋转矩形，得到矩形，点的对应点分别为，记旋转角为．
(1)如图①，当时，求点的坐标；
(2)如图②，当点落在的延长线上时，求点的坐标；
(3)当点落在线段上时，求点的坐标（直接写出结果即可）．
21．（8分）如图，一次函数y＝﹣2x+8与反比例函数(x＞0)的图象交于A(m，6)，B(3，n)两点，与x轴交于D点．
（1）求反比例函数的解析式．
（2）在第一象限内，根据图象直接写出一次函数值大于反比例函数值时自变量x的取值范围．
22．（10分）如图，已知是的直径，是的弦，点在外，连接，的平分线交于点.
（1）若，求证：是的切线；
（2）若，，求弦的长.
23．（10分）已知一个二次函数的图象经过A（0，﹣3），B（1，0），C（m，2m+3），D（﹣1，﹣2）四点，求这个函数解析式以及点C的坐标．
24．（10分）东东玩具商店用500元购进一批悠悠球，很受中小学生欢迎，悠悠球很快售完，接着又用900元购进第二批这种悠悠球，所购数量是第一批数量的1.5倍，但每套进价多了5元．
（1）求第一批悠悠球每套的进价是多少元；
（2）如果这两批悠悠球每套售价相同，且全部售完后总利润不低于25%，那么每套悠悠球的售价至少是多少元？
25．（12分）如图所示，已知扇形AOB的半径为6㎝，圆心角的度数为120°，若将此扇形围成一个圆锥，
则：
（1）求出围成的圆锥的侧面积为多少；
（2）求出该圆锥的底面半径是多少．
26．（12分）如图，某足球运动员站在点O处练习射门．将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y＝at2+5t+c，己知足球飞行0.8s时，离地面的高度为3.5m．
（1）a＝ ，c＝ ；
（2）当足球飞行的时间为多少时，足球离地面最高？最大高度是多少？
（3）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
参考答案
一、选择题（每题4分，共48分）
1、B
2、B
3、B
4、A
5、C
6、C
7、D
8、B
9、D
10、C
11、A
12、D
二、填空题（每题4分，共24分）
13、x＜-2或x＞1
14、1
15、1
16、1
17、
18、．
三、解答题（共78分）
19、（1）①1；②m＞2或m＜0；（2）﹣＜a≤﹣或a＝1．
20、（1）点的坐标为；（2）点的坐标为；（3）点的坐标为．
21、（1） (x＞0)；（2） 1＜x＜1．
22、（1）证明见解析；（2）.
23、y=2x2+x﹣3，C点坐标为（﹣，0）或（2，7）
24、（1）第一批悠悠球每套的进价是25元；（2）每套悠悠球的售价至少是1元．
25、（1）11π；（1）1．
26、（1），；（2）当足球飞行的时间s时，足球离地面最高，最大高度是4.5m；（3）能．