湖南长沙雨花区雅境中学2023-2024学年九上数学期末经典试题含答案

这是一份湖南长沙雨花区雅境中学2023-2024学年九上数学期末经典试题含答案，共8页。试卷主要包含了答题时请按要求用笔，如图，正方形的边长为，点在边上，不等式组的解集在数轴上表示为，如图，中，，则的值为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图所示，的顶点是正方形网格的格点，则的值为（ ）
A．B．C．D．
2．已知点都在双曲线上，且，则的取值范围是（ ）
A．B．C．D．
3．一个盒子中装有2个蓝球，3个红球和若干个黄球，小明通过多次摸球试验后发现，摸取到黄球的频率稳定在0.5左右，则黄球有（ ）个．
A．4B．5C．6D．10
4．如图，⊙O的直径BA的延长线与弦DC的延长线交于点E，且CE＝OB，已知∠DOB＝72°，则∠E等于（ ）
A．18°B．24°C．30°D．26°
5．在平面直角坐标系中，抛物线经过变换后得到抛物线，则这个变换可以是（ ）
A．向左平移2个单位B．向右平移2个单位
C．向左平移8个单位D．向右平移8个单位
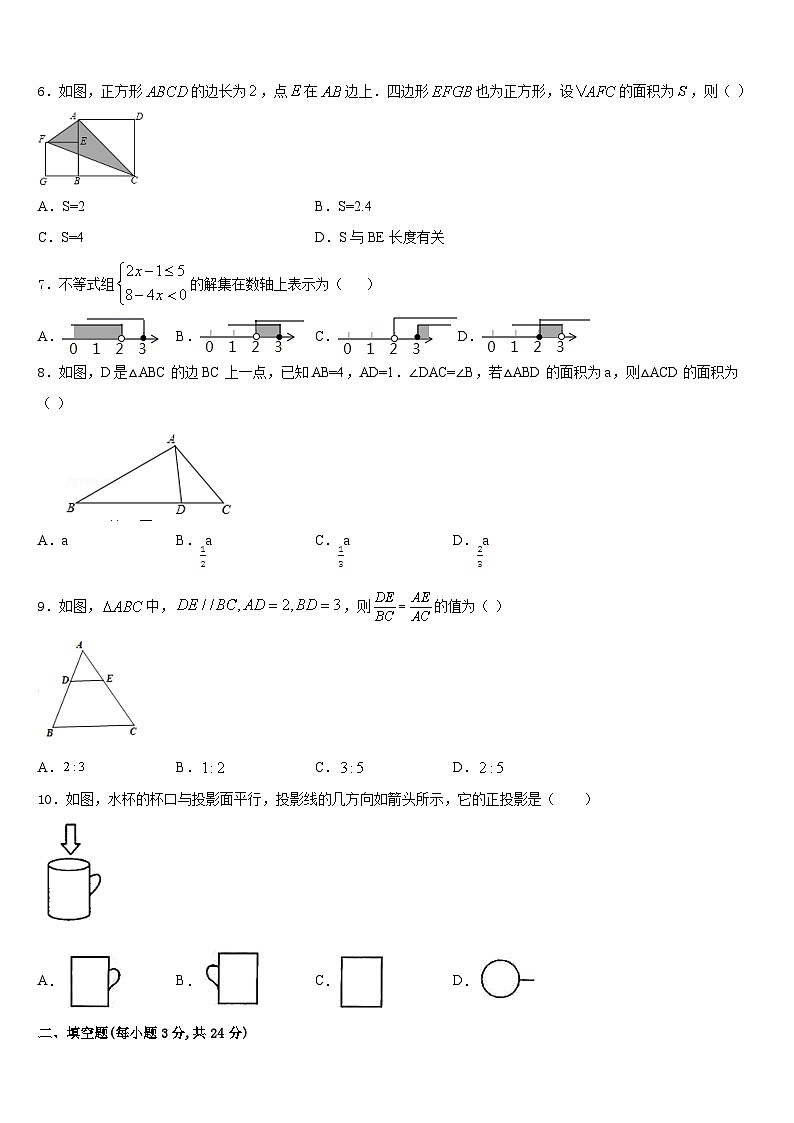
6．如图，正方形的边长为，点在边上．四边形也为正方形，设的面积为，则（ ）
A．S=2B．S=2.4
C．S=4D．S与BE长度有关
7．不等式组的解集在数轴上表示为（ ）
A．B．C．D．
8．如图，D是△ABC的边BC上一点，已知AB=4，AD=1．∠DAC=∠B，若△ABD的面积为a，则△ACD的面积为（ ）
A．aB．aC．aD．a
9．如图，中，，则的值为（ ）
A．B．C．D．
10．如图，水杯的杯口与投影面平行，投影线的几方向如箭头所示，它的正投影是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．如果△ABC∽△DEF，且△ABC的三边长分别为4、5、6，△DEF的最短边长为12，那么△DEF的周长等于_____．
12．我军侦察员在距敌方120m的地方发现敌方的一座建筑物，但不知其高度又不能靠近建筑物物测量，机灵的侦察员将自己的食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住，如图所示．若此时眼睛到食指的距离约为40cm，食指的长约为8cm，则敌方建筑物的高度约是_______m．
13．如图所示的网格是正方形网格，△和△的顶点都是网格线交点，那么∠∠_________°．
14．如图，在中，，点D、E分别在边、上，且，如果，，那么________．
15．如图，在△ABC中，∠C=90°，AC=3，若csA=,则BC的长为________.
16．请写出一个开口向上，并且与y轴交于点（0，－1）的抛物线的表达式：______
17．如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．
18．若两个相似三角形的面积之比为1:4，则它们对应角的角平分线之比为___．
三、解答题(共66分)
19．（10分）已知在△ABC中，AB=AC，∠BAC=α，直线l经过点A（不经过点B或点C），点C关于直线l的对称点为点D，连接BD，CD．
（1）如图1，
①求证：点B，C，D在以点A为圆心，AB为半径的圆上；
②直接写出∠BDC的度数（用含α的式子表示）为 ；
（2）如图2，当α=60°时，过点D作BD的垂线与直线l交于点E，求证：AE=BD；
（3）如图3，当α=90°时，记直线l与CD的交点为F，连接BF．将直线l绕点A旋转的过程中，在什么情况下线段BF的长取得最大值？若AC=2a，试写出此时BF的值．
20．（6分）如图，在一条河流的两岸分别有A、B、C、D四棵景观树，已知AB//CD，某数学活动小组测得∠DAB=45°，∠CBE=73°，AB=10m，CD=30m，请计算这条河的宽度(参考数值：，，)
21．（6分）某小区新建成的住宅楼主体工程已经竣工，只剩下楼体外表需贴瓷砖，已知楼体外表的面积为．
（1）写出每块瓷砖的面积与所需的瓷砖块数（块）之间的函数关系式；
（2）为了使住宅楼的外观更漂亮，开发商决定采用灰、白、蓝三种颜色的瓷砖，每块瓷砖的面积都是，灰、白、蓝瓷砖使用比例是，则需要三种瓷砖各多少块？
22．（8分）年月日商用套餐正式上线.某移动营业厅为了吸引用户，设计了，两个可以自由转动的转盘（如图），转盘被等分为个扇形，分别为红色和黄色；转盘被等分为个扇形，分别为黄色、红色、蓝色，指针固定不动.营业厅规定，每位新用户可分别转动两个转盘各一次，转盘停止后，若指针所指区域颜色相同，则该用户可免费领取通用流量（若指针停在分割线上，则视其指向分割线右侧的扇形）.小王办理业务获得一次转转盘的机会，求他能免费领取通用流量的概率.
A B
23．（8分）如图，在半径为5的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．
（1）当BC=6时，求线段OD的长；
（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．
24．（8分）有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．
（1）求被剪掉阴影部分的面积：
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？
25．（10分）为支持大学生勤工俭学，市政府向某大学生提供了万元的无息贷款用于销售某种自主研发的产品，并约定该学生用经营的利润逐步偿还无息贷款，已知该产品的生产成本为每件元．每天还要支付其他费用元．该产品每天的销售量件与销售单价元关系为．
（1）设每天的利润为元，当销售单价定为多少元时，每天的利润最大？最大利润为多少元？注：每天的利润每天的销售利润一每天的支出费用
（2）若销售单价不得低于其生产成本，且销售每件产品的利润率不能超过，则该学生最快用多少天可以还清无息贷款？
26．（10分）为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生(七、八年级各有600名学生)的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析，过程如下：
收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，1．
八年级：92，74，87，82，72，81，94，83，1，83，80，81，71，81，72，1，82，80，70，2．
整理数据：
分析数据：
应用数据：
(1)由上表填空：a= ，b= ，c= ，d= ．
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、D
3、B
4、B
5、B
6、A
7、B
8、C
9、D
10、D
二、填空题(每小题3分,共24分)
11、1
12、1
13、45
14、
15、1
16、y=x2-1（答案不唯一）．
17、π.
18、1：1
三、解答题(共66分)
19、（1）①详见解析；②α；（2）详见解析；（3）当B、O、F三点共线时BF最长，(+)a
20、m
21、（1）；（2）需要灰瓷砖125000块，白瓷砖250000块、蓝瓷砖为250000块
22、他能免费领取100G100G通用流量的概率为.
23、（1）线段OD的长为1．
（2）存在，DE保持不变．DE=．
24、（1）平方米；（2）米；
25、（1）当销售单价定为25元时，日销售利润最大为200元；（2）该生最快用100天可以还清无息贷款．
26、 (1) 11 ， 10 ， 78 ， 81 ；(2)90人；(3) 八年级的总体水平较好
七年级
0
1
0
a
7
1
八年级
1
0
0
7
b
2
平均数
众数
中位数
七年级
78
75
八年级
78
80.5