湖北省武汉市二中学广雅中学2023-2024学年数学九上期末复习检测试题含答案

这是一份湖北省武汉市二中学广雅中学2023-2024学年数学九上期末复习检测试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是
A．（6，0）B．（6，3）C．（6，5）D．（4，2）
2．化简的结果是（ ）
A．2B．4C．2D．4
3．在下列图形中，既是中心对称图形又是轴对称图形的是( )
A．等边三角形B．圆C．等腰梯形D．直角三角形
4．小思去延庆世界园艺博览会游览，如果从永宁瞻胜、万芳华台、丝路花雨、九州花境四个景点中随机选择一个进行参观，那么他选择的景点恰为丝路花雨的概率为（ ）
A．B．C．D．
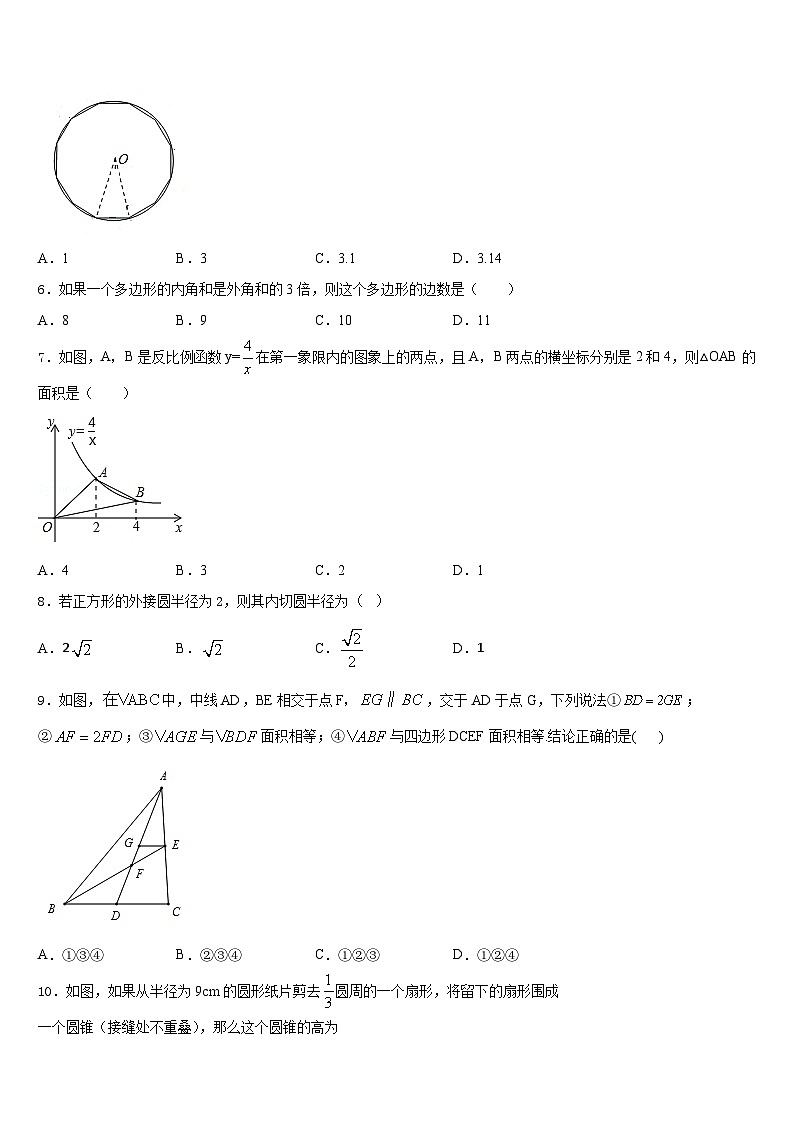
5． “割圆术”是我国古代的一位伟大的数学家刘徽首创的，该割圆术，就是通过不断倍增圆内接正多边形的边数来求出圆周率的一种方法，某同学在学习“割圆术”的过程中，画了一个如图所示的圆的内接正十二边形，若该圆的半径为1，则这个圆的内接正十二边形的面积为（ ）．
A．1B．3C．3.1D．3.14
6．如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）
A．8B．9C．10D．11
7．如图，A，B是反比例函数y=在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4，则△OAB的面积是（ ）
A．4B．3C．2D．1
8．若正方形的外接圆半径为2，则其内切圆半径为（ ）
A．2B．C．D．1
9．如图，中，中线AD，BE相交于点F，，交于AD于点G，下列说法①；②；③与面积相等；④与四边形DCEF面积相等.结论正确的是( )
A．①③④B．②③④C．①②③D．①②④
10．如图，如果从半径为9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成
一个圆锥（接缝处不重叠），那么这个圆锥的高为
A．6cmB．cmC．8cmD．cm
二、填空题(每小题3分,共24分)
11．如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,，按此规律继续下去，则矩形AB2019C2019C2018的面积为_____．
12．二次函数y＝x2的图象如图所示，点A0位于坐标原点，点A1、A、A、…、A在y轴的正半轴上，点B、B、B、…、B在二次函数y＝x2位于第一象限的图象上，若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形，则△ABA的边长＝____________．
13．反比例函数与在第一象限内的图象如图所示，轴于点，与两个函数的图象分别相交于两点，连接，则的面积为_________ ．
14．已知二次函数（a是常数，a≠0），当自变量x分别取-6、-4时，对应的函数值分别为y1、y2，那么y1、y2的大小关系是：y1__ y2（填“>”、“<”或“=”）．
15．如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作当与正方形ABCD的边相切时，BP的长为______．
16．如图,P是∠α的边OA上一点，且点P的坐标为（3，4），则=____________.
17．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝1．下列结论：其中正确结论有_____．
①abc＞0；②16a+4b+c＜0；③4ac﹣b2＜8a；④＜a；⑤b＜c．
18．已知函数（为常数），若从中任取值，则得到的函数是具有性质“随增加而减小”的一次函数的概率为___________.
三、解答题(共66分)
19．（10分）如图，A，B，C是⊙O上的点，，半径为5，求BC的长．
20．（6分）解下列两题：
(1)已知，求的值；
(2)已知α为锐角，且2sinα=4cs30°﹣tan60°，求α的度数．
21．（6分）如图，BD为⊙O的直径，点A是劣弧BC的中点，AD交BC于点E，连结AB．
(1)求证：AB2=AE·AD；
(2)若AE=2，ED=4，求图中阴影的面积．
22．（8分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与两坐标轴分别交于点A、B、C，直线y＝﹣x+4经过点B，与y轴交点为D，M（3，﹣4）是抛物线的顶点．
（1）求抛物线的解析式．
（2）已知点N在对称轴上，且AN+DN的值最小．求点N的坐标．
（3）在（2）的条件下，若点E与点C关于对称轴对称，请你画出△EMN并求它的面积．
（4）在（2）的条件下，在坐标平面内是否存在点P，使以A、B、N、P为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
23．（8分）某超市销售一种饮料， 每瓶进价为元，当每瓶售价元时，日均销售量瓶.经市场调查表明，每瓶售价每增加元，日均销售量减少瓶.
（1）当每瓶售价为元时，日均销售量为 瓶；
（2）当每瓶售价为多少元时，所得日均总利润为元；
（3）当每瓶售价为多少元时，所得日均总利润最大？最大日均总利润为多少元？
24．（8分）如图，点在以线段为直径的圆上，且，点在上，且于点，是线段的中点，连接、.
（1）若，，求的长；
（2）求证：．
25．（10分）如图，在中，，，圆是的外接圆.
（1）求圆的半径；
（2）若在同一平面内的圆也经过、两点，且，请直接写出圆的半径的长.
26．（10分）已知二次函数图象的顶点在原点，对称轴为轴.直线的图象与二次函数的图象交于点和点（点在点的左侧）
（1）求的值及直线解析式；
（2）若过点的直线平行于直线且直线与二次函数图象只有一个交点，求交点的坐标.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、B
4、B
5、B
6、A
7、B
8、B
9、D
10、B
二、填空题(每小题3分,共24分)
11、
12、1
13、
14、>
15、3或
16、
17、①③④．
18、
三、解答题(共66分)
19、＝8
20、 (1) 6；(2) 锐角α=30°
21、 (1)见解析;(2) 2π-3.
22、（1）y＝x2﹣6x+5；（2）N(3，)；（3）画图见解析，S△EMN＝；（4）存在，满足条件的点P的坐标为（3，﹣）或（7，）或（﹣1，）．
23、（1）；（2）元或元；（3）元时利润最大，最大利润元
24、（1）5 ； （2）见解析
25、（1）；（2）或
26、（1）m=，；（2）