安徽省六区联考2023-2024学年九年级数学第一学期期末学业水平测试模拟试题含答案

这是一份安徽省六区联考2023-2024学年九年级数学第一学期期末学业水平测试模拟试题含答案，共7页。试卷主要包含了二次函数的最小值是，已知α为锐角，且sin，一元二次方程的根的情况是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．把抛物线向下平移2个单位，再向右平移1个单位，所得到的抛物线是
A．B．C．D．
2．如图，在正方形ABCD中，H是对角线BD的中点，延长DC至E，使得DE=DB，连接BE，作DF⊥BE交BC于点G，交BE于点F，连接CH、FH，下列结论：（1）HC=HF；（2）DG=2EF；（3）BE·DF=2CD2；（4）S△BDE=4S△DFH；（5）HF∥DE，正确的个数是（ ）
A．5B．4C．3D．2
3．如图，将直尺与含30°角的三角尺放在一起，若∠1＝25°，则∠2的度数是（ ）
A．30°B．45°C．55°D．60°
4．已知关于的一元二次方程的两个根分别是，，且满足，则的值是（ ）
A．0B．C．0或D．或0
5．二次函数的最小值是 （ ）
A．2B．2C．1D．1
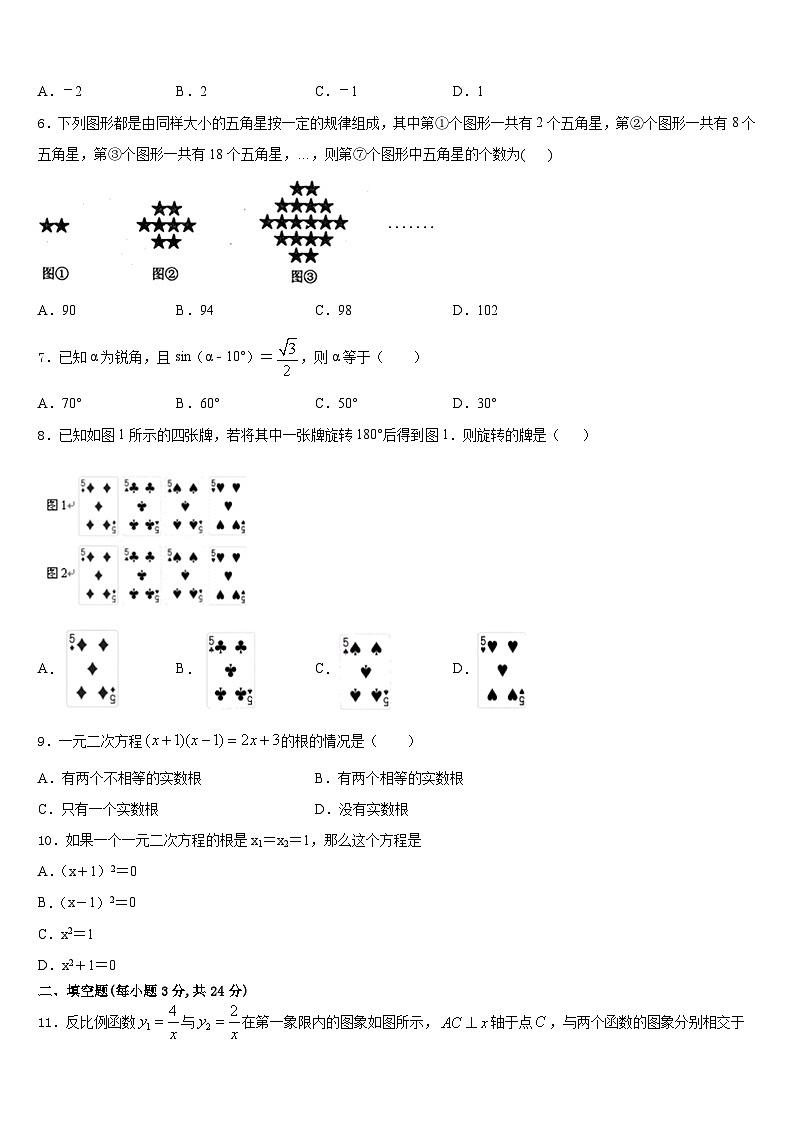
6．下列图形都是由同样大小的五角星按一定的规律组成，其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五角星，…，则第⑦个图形中五角星的个数为( )
A．90B．94C．98D．102
7．已知α为锐角，且sin（α﹣10°）＝，则α等于（ ）
A．70°B．60°C．50°D．30°
8．已知如图1所示的四张牌，若将其中一张牌旋转180°后得到图1．则旋转的牌是（ ）
A．B．C．D．
9．一元二次方程的根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．只有一个实数根D．没有实数根
10．如果一个一元二次方程的根是x1＝x2＝1，那么这个方程是
A．（x＋1）2＝0
B．（x－1）2＝0
C．x2＝1
D．x2＋1＝0
二、填空题(每小题3分,共24分)
11．反比例函数与在第一象限内的图象如图所示，轴于点，与两个函数的图象分别相交于两点，连接，则的面积为_________ ．
12．若m是关于x的方程x2-2x-3=0的解，则代数式4m-2m2+2的值是______．
13．甲、乙两人在100米短跑训练中，某5次的平均成绩相等，甲的方差是0.12，乙的方差是0.05，这5次短跑训练成绩较稳定的是_____．（填“甲”或“乙”）
14．如果将抛物线向上平移，使它经过点那么所得新抛物线的解析式为____________.
15．把一袋黑豆中放入红豆100粒，搅匀后取出100粒豆子，其中红豆5粒，则该袋中约有黑豆_______粒．
16．如图，⊙O的半径为2，弦BC=2，点A是优弧BC上一动点（不包括端点），△ABC的高BD、CE相交于点F，连结ED．下列四个结论：
①∠A始终为60°；
②当∠ABC=45°时，AE=EF；
③当△ABC为锐角三角形时，ED=；
④线段ED的垂直平分线必平分弦BC．
其中正确的结论是_____．（把你认为正确结论的序号都填上）
17．如果函数 是二次函数，那么k的值一定是________．
18．如图所示，个边长为1的等边三角形，其中点，，，，…在同一条直线上，若记的面积为，的面积为，的面积为，…，的面积为，则______.
三、解答题(共66分)
19．（10分）篮球课上，朱老师向学生详细地讲解传球的要领时，叫甲、乙、丙、丁四位同学配合朱老师进行传球训练，朱老师把球传给甲同学后，让四位同学相互传球，其他人观看体会，当甲同学第一个传球时，求甲同学传给下一个同学后，这个同学再传给甲同学的概率
20．（6分）一个不透明的布袋里装有3个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率.
(1)布袋里红球有多少个？
(2)先从布袋中摸出1个球后不放回，再摸出1个球，求出两次都摸到白球的概率.
21．（6分）如图，某农场准备围建一个中间隔有一道篱笆的矩形花圃，现有长为米的篱笆，一边靠墙，若墙长米，设花圃的一边为米；面积为平方米．
（1）求与的函数关系式及值的取值范围；
（2）若边不小于米，这个花圃的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．
22．（8分）如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且经过A(1,0)，C(0，3)两点，与x轴的另一个交点为B．
(1)若直线y＝mx＋n经过B，C两点，求直线BC和抛物线的解析式；
(2)在抛物线的对称轴x＝－1 上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标．
23．（8分）某公司开发一种新的节能产品，工作人员对销售情况进行了调查，图中折线表示月销售量(件)与销售时间(天)之间的函数关系，已知线段表示函数关系中，时间每增加天，月销售量减少件，求与间的函数表达式．
24．（8分）某手机店销售部型和部型手机的利润为元，销售部型和部型手机的利润为元.
(1)求每部型手机和型手机的销售利润；
(2)该手机店计划一次购进，两种型号的手机共部，其中型手机的进货量不超过型手机的倍，设购进型手机部，这部手机的销售总利润为元.
①求关于的函数关系式；
②该手机店购进型、型手机各多少部，才能使销售总利润最大？
(3)在(2)的条件下，该手机店实际进货时，厂家对型手机出厂价下调元，且限定手机店最多购进型手机部，若手机店保持同种手机的售价不变，设计出使这部手机销售总利润最大的进货方案.
25．（10分）如图，是⊙的直径，是⊙的切线，点为切点，与⊙交于点，点是的中点，连结．
（1）求证：是⊙的切线；
（2）若，，求阴影部分的面积．
26．（10分）如图，等边△ABC内接于⊙O，P是上任一点（点P不与点A、B重合），连AP、BP，过点C作CM∥BP交PA的延长线于点M．
（1）填空：∠APC= 度，∠BPC= 度；
（2）求证：△ACM≌△BCP；
（3）若PA=1，PB=2，求梯形PBCM的面积．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、C
4、C
5、B
6、C
7、A
8、A
9、A
10、B
二、填空题(每小题3分,共24分)
11、
12、-1
13、乙
14、
15、1
16、①②③④
17、-1
18、
三、解答题(共66分)
19、．
20、 (1)红球的个数为2个；(2).
21、（1）；（2）当时，有最大值，最大值是，当时，有最小值，最小值是
22、（1）y＝－x2－2x＋3，y＝x＋3；（2）M(－1，2)．
23、．
24、 (1)每部型手机的销售利润为元，每部型手机的销售利润为元；(2)①；②手机店购进部型手机和部型手机的销售利润最大；(3)手机店购进部型手机和部型手机的销售利润最大.
25、（1）见解析；（2）．
26、（1）60；60；（2）证明见解析；（3）.