2023-2024学年江苏省金坛市尧塘，河头，水北中学九上数学期末质量跟踪监视模拟试题含答案

这是一份2023-2024学年江苏省金坛市尧塘，河头，水北中学九上数学期末质量跟踪监视模拟试题含答案，共7页。试卷主要包含了抛物线的顶点坐标是，在平面直角坐标系中，以点，下列函数中，图象不经过点等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题(每小题3分,共30分)
1．将点A（﹣3，4）绕原点顺时针方向旋转180°后得到点B，则点B的坐标为（ ）
A．（3，﹣4）B．（﹣4，3）C．（﹣4，﹣3）D．（﹣3，﹣4）
2．如图，是的直径，弦于，连接、，下列结论中不一定正确的是（ ）
A．B．C．D．
3．如图所示，四边形OABC是正方形，边长为6，点A、C分别在x轴、y轴的正半轴上，点D在OA上，且D点的坐标为(2，0)，P是OB上一动点，则PA＋PD的最小值为( )
A．2B．C．4D．6
4．在一次酒会上，每两人都只碰一次杯，如果一共碰杯55次，则参加酒会的人数为（ ）
A．9人B．10人C．11人D．12人
5．将函数的图象向左平移个单位，再向下平移个单位，可得到的抛物线是：（ ）
A．B．C．D．
6．抛物线的顶点坐标是（ ）
A．(2, 1)B．(2, -1)C．(-2, 1)D．(-2, -1)
7．在平面直角坐标系中，以点（3，2）为圆心、2为半径的圆，一定（ ）
A．与x轴相切，与y轴相切B．与x轴相切，与y轴相离
C．与x轴相离，与y轴相切D．与x轴相离，与y轴相离
8．下列函数中，图象不经过点（2，1）的是（ ）
A．y=﹣x2+5B．y=C．y=xD．y=﹣2x+3
9．在一个不透明的塑料袋中装有红色、白色球共40个，除颜色外其它都相同，小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中红色球可能 （ ）
A．4个B．6个C．34个D．36个
10．如图，在平面直角坐标系中，菱形ABCD的顶点A(3，0)，顶点B在y轴正半轴上，顶点D在x轴负半轴上，若抛物线y=－x2－5x+c经过点B、C，则菱形ABCD的面积为（ ）
A．15B．20C．25D．30
二、填空题(每小题3分,共24分)
11．__________．
12．若，则＝_____．
13．若m2﹣2m﹣1=0，则代数式2m2﹣4m+3的值为 ．
14．已知圆锥的底面半径是3cm，母线长是5cm，则圆锥的侧面积为_____cm1．（结果保留π）
15．如图， 圆的直径垂直于弦，垂足是，，，的长为__________．
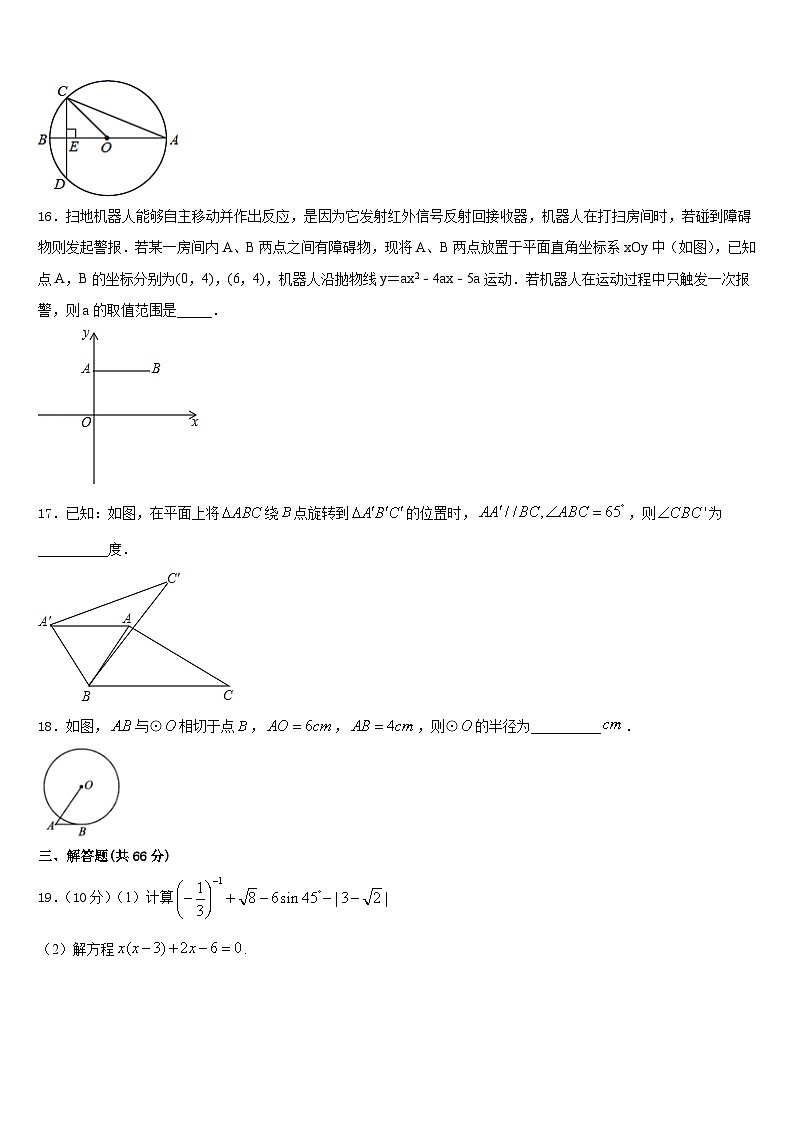
16．扫地机器人能够自主移动并作出反应，是因为它发射红外信号反射回接收器，机器人在打扫房间时，若碰到障碍物则发起警报．若某一房间内A、B两点之间有障碍物，现将A、B两点放置于平面直角坐标系xOy中（如图），已知点A，B的坐标分别为(0，4)，(6，4)，机器人沿抛物线y＝ax2﹣4ax﹣5a运动．若机器人在运动过程中只触发一次报警，则a的取值范围是_____．
17．已知：如图，在平面上将绕点旋转到的位置时，，则为__________度．
18．如图，与⊙相切于点，，，则⊙的半径为__________．
三、解答题(共66分)
19．（10分）（1）计算
（2）解方程.
20．（6分）已知二次函数y＝x2－2x－1．
（1）求图象的对称轴、顶点坐标；
（2）当x为何值时，y随x的增大而增大？
21．（6分）如图，点A、B、C在⊙O上，用无刻度的直尺画图．
（1）在图①中，画一个与∠B互补的圆周角；
（2）在图②中，画一个与∠B互余的圆周角．
22．（8分）如图，在中，∠A=90°，AB=12cm，AC=6cm，点P沿AB边从点A开始向点B以每秒2cm的速度移动，点Q沿CA边从点C开始向点A以每秒1cm的速度移动，P、Q同时出发，用t表示移动的时间．
（1）当t为何值时，△QAP为等腰直角三角形?
（2）当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似?
23．（8分）某环保器材公司销售一种市场需求较大的新型产品，已知每件产品的进价为40元，经销过程中测出销售量y（万件）与销售单价x（元）存在如图所示的一次函数关系，每年销售该种产品的总开支z（万元）（不含进价）与年销量y（万件）存在函数关系z=10y+42.1．
（1）求y关于x的函数关系式；
（2）写出该公司销售该种产品年获利w（万元）关于销售单价x（元）的函数关系式；（年获利=年销售总金额一年销售产品的总进价一年总开支金额）当销售单价x为何值时，年获利最大?最大值是多少?
（3）若公司希望该产品一年的销售获利不低于17.1万元，请你利用（2）小题中的函数图象帮助该公司确定这种产品的销售单价的范围．在此条件下要使产品的销售量最大，你认为销售单价应定为多少元?
24．（8分）一次函数与反比例函数的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点D．
（1）求一次函数与反比例函数的表达式；
（2）过点B作BC⊥y轴，垂足为C，连接AC交x轴于点E，求△AED的面积S．
25．（10分）如图示，是的直径，点是半圆上的一动点（不与，重合），弦平分，过点作交射线于点.
（1）求证：与相切：
（2）若，，求长；
（3）若，长记为，长记为，求与之间的函数关系式，并求出的最大值.
26．（10分）如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB．
⑴求证：BE是⊙O的切线；
⑵若BC=，AC=5，求圆的直径AD的长．
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、A
4、C
5、C
6、C
7、B
8、D
9、B
10、B
二、填空题(每小题3分,共24分)
11、
12、
13、1
14、15π
15、
16、﹣＜a＜
17、1
18、
三、解答题(共66分)
19、（1）-6；（2）
20、（1） 对称轴是x=1，顶点坐标是（1，-4）；（2）当x>1时，y随x的增大而增大．
21、（1）见解析；（2）见解析
22、（1）；（2）或．
23、（1）；（2）当x=81元时，年获利最大值为80万元；（3）销售单价定为70元
24、（1），；（2）．
25、（1）详见解析；（2）4；（3）
26、（1）详见解析；（2）1