【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题01幂函数、指数函数与对数函数全章复习攻略与难点强化训练-练习.zip

这是一份【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题01幂函数、指数函数与对数函数全章复习攻略与难点强化训练-练习.zip，文件包含寒假作业沪教版2020高中数学高一寒假巩固提升训练专题01幂函数指数函数与对数函数全章复习攻略与难点强化训练原卷版docxdocx、寒假作业沪教版2020高中数学高一寒假巩固提升训练专题01幂函数指数函数与对数函数全章复习攻略与难点强化训练解析版docxdocx等2份试卷配套教学资源，其中试卷共64页， 欢迎下载使用。


一．幂函数的概念、解析式、定义域、值域
【知识点归纳】
幂函数的定义：一般地，函数y＝xa叫做幂函数，其中x是自变量，a是常数．
解析式：y＝xa＝
定义域：当a为不同的数值时，幂函数的定义域的不同情况如下：
1．如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根据q的奇偶性来确定，即如果q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数；
2．如果同时q为奇数，则函数的定义域为不等于0的所有实数．
当x为不同的数值时，幂函数的值域的不同情况如下：
1．在x大于0时，函数的值域总是大于0的实数．
2．在x小于0时，则只有同时q为奇数，函数的值域为非零的实数．
而只有a为正数，0才进入函数的值域．
由于x大于0是对a的任意取值都有意义的．
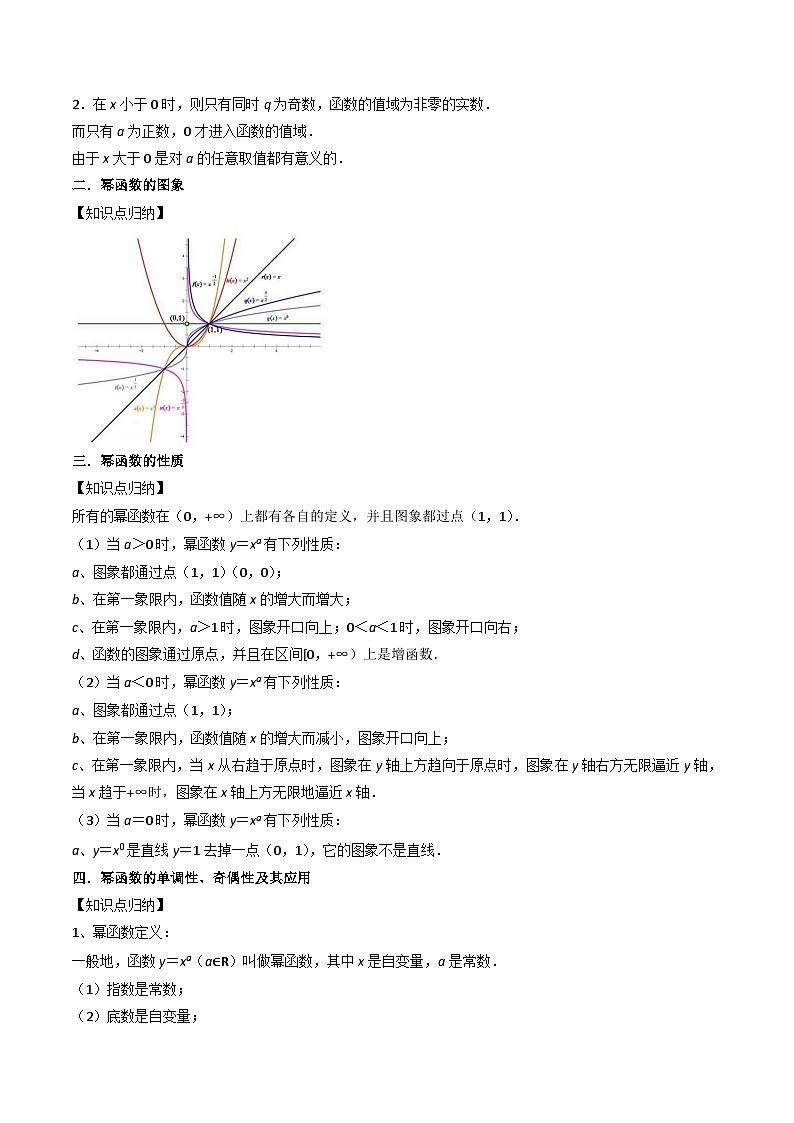
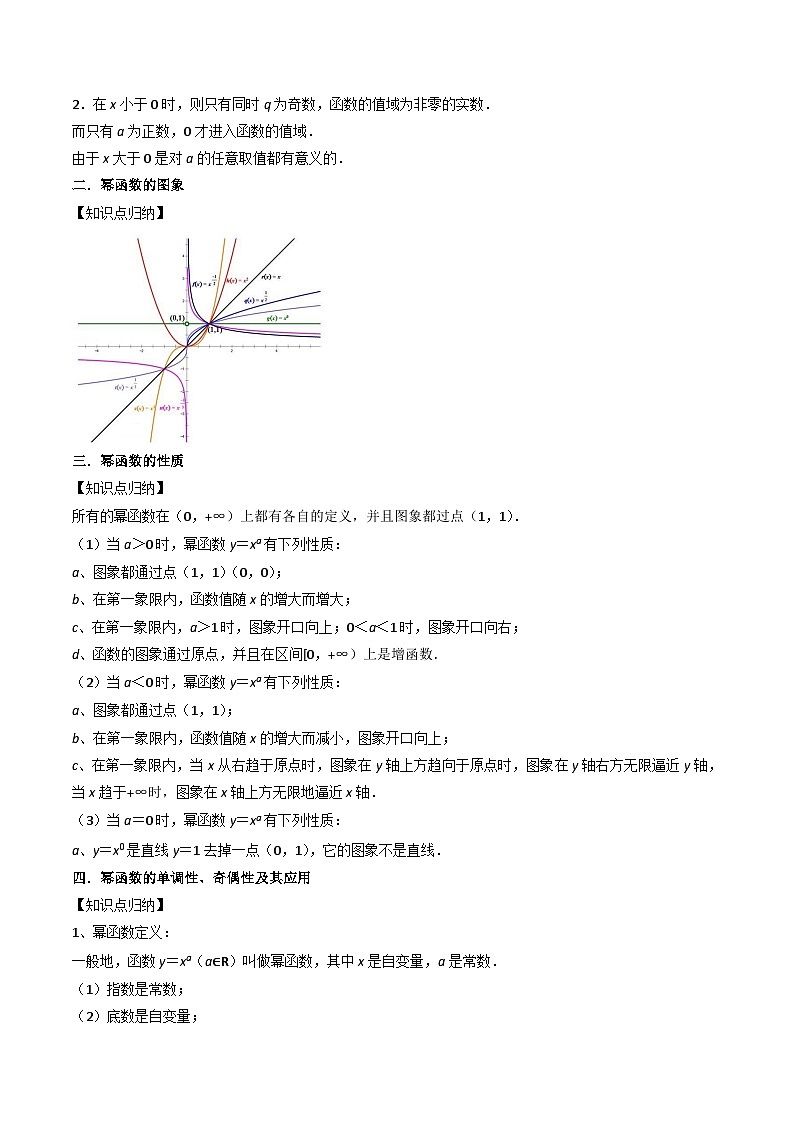
二．幂函数的图象
【知识点归纳】
三．幂函数的性质
【知识点归纳】
所有的幂函数在（0，+∞）上都有各自的定义，并且图象都过点（1，1）．
（1）当a＞0时，幂函数y＝xa有下列性质：
a、图象都通过点（1，1）（0，0）；
b、在第一象限内，函数值随x的增大而增大；
c、在第一象限内，a＞1时，图象开口向上；0＜a＜1时，图象开口向右；
d、函数的图象通过原点，并且在区间[0，+∞）上是增函数．
（2）当a＜0时，幂函数y＝xa有下列性质：
a、图象都通过点（1，1）；
b、在第一象限内，函数值随x的增大而减小，图象开口向上；
c、在第一象限内，当x从右趋于原点时，图象在y轴上方趋向于原点时，图象在y轴右方无限逼近y轴，当x趋于+∞时，图象在x轴上方无限地逼近x轴．
（3）当a＝0时，幂函数y＝xa有下列性质：
a、y＝x0是直线y＝1去掉一点（0，1），它的图象不是直线．
四．幂函数的单调性、奇偶性及其应用
【知识点归纳】
1、幂函数定义：
一般地，函数y＝xa（a∈R）叫做幂函数，其中x是自变量，a是常数．
（1）指数是常数；
（2）底数是自变量；
（3）函数式前的系数都是1；
（4）形式都是y＝xa，其中a是常数．
2、幂函数与指数函数的对比
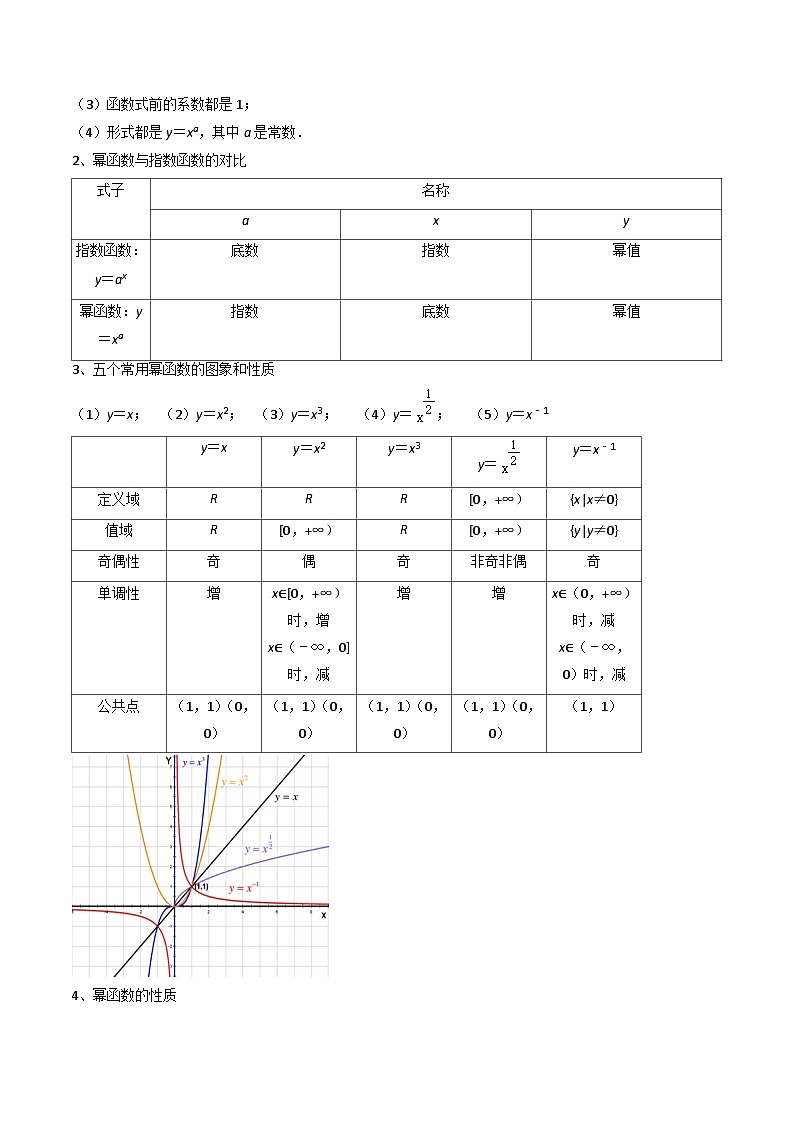
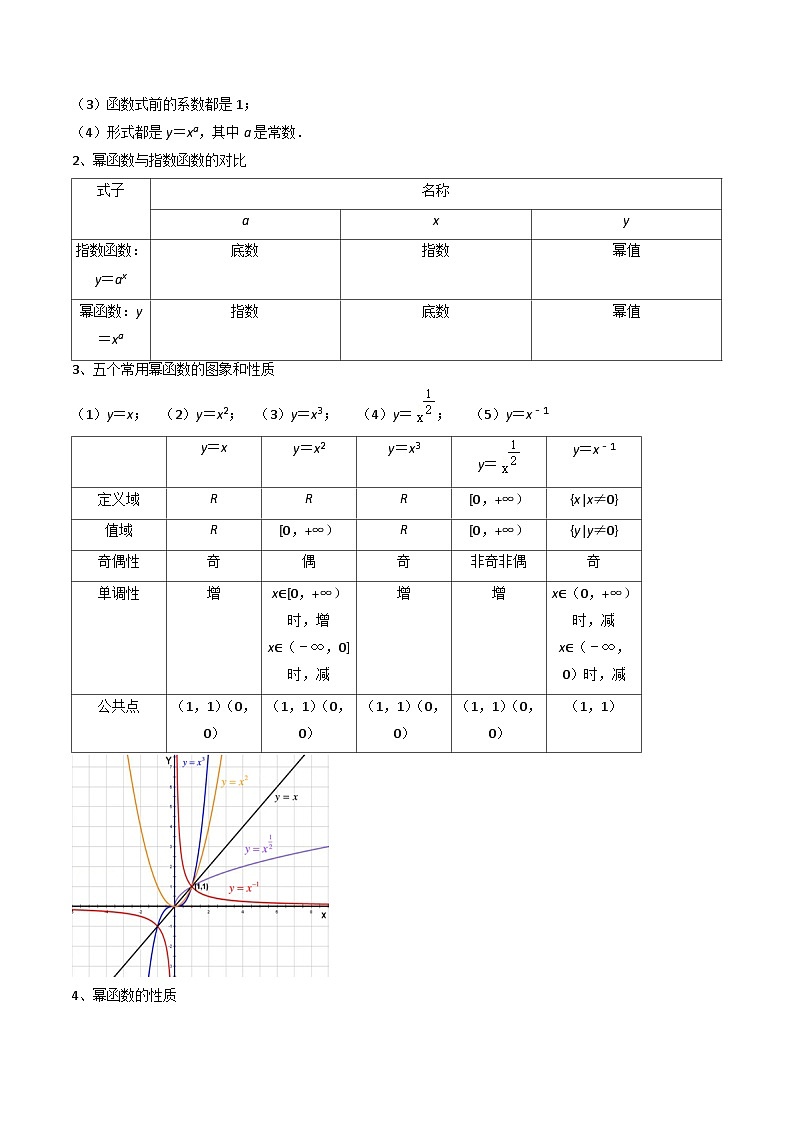
3、五个常用幂函数的图象和性质
（1）y＝x； （2）y＝x2； （3）y＝x3； （4）y＝； （5）y＝x﹣1
4、幂函数的性质
（1）所有的幂函数在（0，+∞）都有定义，并且函数图象都通过点（1，1）．
（2）如果a＞0，则幂函数的图象过点（0，0），（1，1），并在[0，+∞）上为增函数．
（3）如果a＜0，则幂函数的图象过点（1，1），并在（0，+∞）上为减函数．
（4）当a为奇数时，幂函数为奇函数，当a为偶数时，幂函数为偶函数．
五．指数函数的定义、解析式、定义域和值域
【知识点归纳】
指数函数的解析式、定义、定义域、值域
1、指数函数的定义：
一般地，函数y＝ax（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R，值域是（0，+∞）．
2、指数函数的解析式：
y＝ax（a＞0，且a≠1）
3、理解指数函数定义，需注意的几个问题：
①因为a＞0，x是任意一个实数时，ax是一个确定的实数，所以函数的定义域为实数集R．
②规定底数a大于零且不等于1的理由：
如果a＝0，当x＞0时，ax恒等于0；当x≤0时，ax无意义；
如果a＜0，比如y＝（﹣4）x，这时对于x＝，x＝在实数范围内函数值不存在．
如果a＝1，y＝1x＝1是一个常量，对它就没有研究的必要，
为了避免上述各种情况，所以规定a＞0且a≠1．
六．指数函数的图象与性质
【知识点的认识】
1、指数函数y＝ax（a＞0，且a≠1）的图象和性质：
2、底数对指数函数的影响：
①在同一坐标系内分别作函数的图象，易看出：当a＞l时，底数越大，函数图象在第一象限越靠近y轴；同样地，当0＜a＜l时，底数越小，函数图象在第一象限越靠近x轴．
②底数对函数值的影响如图．
③当a＞0，且a≠l时，函数y＝ax 与函数y＝的图象关于y轴对称．
3、利用指数函数的性质比较大小：
若底数相同而指数不同，用指数函数的单调性比较：
若底数不同而指数相同，用作商法比较；
若底数、指数均不同，借助中间量，同时要注意结合图象及特殊值．
七．指数型复合函数的性质及应用
【知识点归纳】
指数型复合函数性质及应用：
指数型复合函数的两个基本类型：y＝f（ax）与y＝af（x）
复合函数的单调性，根据“同增异减”的原则处理
U＝g（x） y＝au y＝ag（x）
增 增 增
减 减 增
增 减 减
减 增 减．
八．指数函数的单调性与特殊点
【知识点归纳】
1、指数函数单调性的讨论，一般会以复合函数的形式出现，所以要分开讨论，首先讨论a的取值范围即a＞1，0＜a＜1的情况．再讨论g（x）的增减，然后遵循同增、同减即为增，一减一增即为减的原则进行判断．
2、同增同减的规律：
（1）y＝ax 如果a＞1，则函数单调递增；
（2）如果0＜a＜1，则函数单调递减．
3、复合函数的单调性：
（1）复合函数为两个增函数复合：那么随着自变量X的增大，Y值也在不断的增大；
（2）复合函数为两个减函数的复合：那么随着内层函数自变量X的增大，内层函数的Y值就在不断的减小，而内层函数的Y值就是整个复合函数的自变量X．因此，即当内层函数自变量X的增大时，内层函数的Y值就在不断的减小，即整个复合函数的自变量X不断减小，又因为外层函数也为减函数，所以整个复合函数的Y值就在增大．因此可得“同增”若复合函数为一增一减两个函数复合：内层函数为增函数，则若随着内层函数自变量X的增大，内层函数的Y值也在不断的增大，即整个复合函数的自变量X不断增大，又因为外层函数为减函数，所以整个复合函数的Y值就在减小．反之亦然，因此可得“异减”．
九．指数函数的实际应用
【知识点归纳】
指数函数图象的应用：
函数的图象是直观地表示函数的一种方法．函数的很多性质，可以从图象上一览无余．数形结合就是几何与代数方法紧密结合的一种数学思想．指数函数的图象通过平移、翻转等变可得出一般函数的图象．利用指数函数的图象，可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题．
十．指数式与对数式的互化
【知识点归纳】
ab＝N⇔lgaN＝b；
algaN＝N；lgaaN＝N
指数方程和对数方程主要有以下几种类型：
（1）af（x）＝b⇔f（x）＝lgab；lgaf（x）＝b⇔f（x）＝ab（定义法）
（2）af（x）＝ag（x）⇔f（x）＝g（x）；lgaf（x）＝lgag（x）⇔f（x）＝g（x）＞0（同底法）
（3）af（x）＝bg（x）⇔f（x）lgma＝g（x）lgmb；（两边取对数法）
（4）lgaf（x）＝lgbg（x）⇔lgaf（x）＝；（换底法）
（5）Algx+Blgax+C＝0（A（ax）2+Bax+C＝0）（设t＝lgax或t＝ax）（换元法）
十一．对数的运算性质
【知识点的认识】
对数的性质：①＝N；②lgaaN＝N（a＞0且a≠1）．
lga（MN）＝lgaM+lgaN； lga＝lgaM﹣lgaN；
lgaMn＝nlgaM； lga＝lgaM．
十二．对数函数的定义
【知识点归纳】
一般地，如果a（a＞0，且a≠1）的b次幂等于N，那么数b叫做以a为底N的对数，记作lgaN＝b，其中a叫做对数的底数，N叫做真数．即ab＝N，lgaN＝b．
底数则要大于0且不为1．
十三．对数函数的定义域
【知识点归纳】
一般地，我们把函数y＝lgax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R．
十四．对数函数的值域与最值
【知识点归纳】
一般地，我们把函数y＝lgax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R．
定点：函数图象恒过定点（1，0）
十五．对数值大小的比较
【知识点归纳】
1、若两对数的底数相同，真数不同，则利用对数函数的单调性来比较．
2、若两对数的底数和真数均不相同，通常引入中间变量（1，﹣1，0）进行比较
3、若两对数的底数不同，真数也不同，则利用函数图象或利用换底公式化为同底的再进行比较．（画图的方法：在第一象限内，函数图象的底数由左到右逐渐增大）
十六．对数函数的图象与性质
【知识点归纳】
十七．对数函数的单调性与特殊点
【知识点归纳】
对数函数的单调性和特殊点：
1、对数函数的单调性
当a＞1时，y＝lgax在（0，+∞）上为增函数
当0＜a＜1时，y＝lgax在（0，+∞）上为减函数
2、特殊点
对数函数恒过点（1，0）
十八．指数函数与对数函数的关系
【知识点归纳】
指数函数和对数函数的关系：
（1）对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y＝x对称．
（2）它们都是单调函数，都不具有奇偶性．当a＞l时，它们是增函数；当O＜a＜l时，它们是减函数．
（3）指数函数与对数函数的联系与区别：
十九．反函数
【知识点归纳】
【定义】一般地，设函数y＝f（x）（x∈A）的值域是C，根据这个函数中x，y 的关系，用y把x表示出，得到x＝g（y）．若对于y在中的任何一个值，通过x＝g（y），x在A中都有唯一的值和它对应，那么，x＝g（y）就表示y是自变量，x是因变量是y的函数，这样的函数y＝g（x）（y∈C）叫做函数y＝f（x）（x∈A）的反函数，记作y＝f（﹣1）（x） 反函数y＝f（﹣1）（x）的定义域、值域分别是函数y＝f（x）的值域、定义域．
【性质】
反函数其实就是y＝f（x）中，x和y互换了角色
（1）函数f（x）与他的反函数f﹣1（x）图象关于直线y＝x对称；函数及其反函数的图形关于直线y＝x对称
（2）函数存在反函数的重要条件是，函数的定义域与值域是一一映射；
（3）一个函数与它的反函数在相应区间上单调性一致；
（4）大部分偶函数不存在反函数（当函数y＝f（x），定义域是{0} 且 f（x）＝C （其中C是常数），则函数f（x）是偶函数且有反函数，其反函数的定义域是{C}，值域为{0} ）．奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数．若一个奇函数存在反函数，则它的反函数也是奇函数．
（5）一切隐函数具有反函数；
（6）一段连续的函数的单调性在对应区间内具有一致性；
（7）严格增（减）的函数一定有严格增（减）的反函数【反函数存在定理】；
（8）反函数是相互的且具有唯一性；
（9）定义域、值域相反对应法则互逆（三反）；
（10）原函数一旦确定，反函数即确定（三定）（在有反函数的情况下，即满足（2））．
一．幂函数的概念、解析式、定义域、值域（共7小题）
1．（2023秋•普陀区校级期中）下列函数是幂函数的是（ ）
A．B．y＝2xC．y＝2x2D．y＝﹣x﹣1
2．（2023秋•嘉定区校级期中）若幂函数y＝xα的图像经过点，则此幂函数的表达式是 ．
3．（2023秋•静安区校级期中）若幂函数y＝xa的图像经过点（2，2），则a＝ ．
4．（2023秋•青浦区校级期中）幂函数y＝xa在x＞1时的图像位于直线y＝x的下方，则a的取值范围是 ．
5．（2023秋•宝山区校级期中）已知函数（a＞0且a≠1）的图象恒过定点A，若幂函数y＝g（x）的图象也经过该点，则＝ ．
6．（2023秋•徐汇区校级期中）幂函数y＝xa，当a取不同的正数时，在区间[0，1]上它们的图象是一组美丽的曲线（如图），设点A（1，0），B（0，1），连接AB，线段AB恰好被其中的两个幂函数y＝xa，y＝xb的图象三等分，即有BM＝MN＝NA，那么ab＝ ．
7．（2023秋•黄浦区校级期中）已知函数是幂函数，且函数图象不经过第二象限，则实数m的值为 ．
二．幂函数的图象（共2小题）
8．（2023•黄浦区校级模拟）如图所示是函数（m，n均为正整数且m，n互质）的图象，则（ ）
A．m，n是奇数且
B．m是偶数，n是奇数，且
C．m是偶数，n是奇数，且
D．m，n是奇数，且
9．（2023秋•杨浦区校级期中）函数的图象是（ ）
A．B．
C．D．
三．幂函数的性质（共6小题）
10．（2023秋•宝山区校级期中）幂函数y＝（m2﹣m﹣1）•x﹣5m﹣3，当x∈（0，+∞）时为减函数，则实数m的值为（ ）
A．m＝2B．m＝﹣1C．m＝﹣1或m＝2D．m≠
11．（2023秋•奉贤区期中）下列幂函数在区间（0，+∞）上是严格增函数，且图像关于原点成中心对称的有 ．（请填入全部正确的序号）
①； ②；③；④
12．（2023秋•静安区校级期中）已知幂函数①y＝，②y＝，③y＝x3，④y＝，其中图象关于y轴对称的是 .（填写全部正确的编号）
13．（2023秋•普陀区校级期中）已知幂函数f（x）＝（m2+4m+4）xm+2在（0，+∞）上单调递减．
（1）求m的值；
（2）若（2a﹣1）﹣m＜（a+3）﹣m，求a的取值范围．
14．（2023秋•静安区校级期中）已知幂函数（m∈Z）满足：①在区间（0，+∞）上是严格增函数；②函数图像关于原点对称．
（1）求同时满足①②的幂函数f（x）的表达式．
（2）在（1）条件下，y＝f（x）图像先向左平移了2个单位，再向上平移了1个单位，恰好和函数y＝g（x）的图像重合，求函数y＝g（x）的表达式．
15．（2023秋•静安区校级期中）已知幂函数f（x）＝（m2﹣5m+5）xm﹣2的图象关于点（0，0）对称．
（1）求该幂函数f（x）的解析式；
（2）设函数g（x）＝|f（x）|，在如图的坐标系中作出函数g（x）的图象；
（3）直接写出函数g（x）的单调区间．
四．幂函数的单调性、奇偶性及其应用（共2小题）
16．（2020秋•天心区校级期末）下列大小关系，正确的是（ ）
A．0.993.3＜0.994.5B．lg20.8＜lg3π
C．0.535.2＜0.355.2D．1.70.3＜0.93.1
17．（2020秋•金山区校级月考）若（m+1）＜（3﹣2m），则实数m的取值范围 ．
五．指数函数的定义、解析式、定义域和值域（共4小题）
18．（2023秋•杨浦区校级期中）对任意x≤1，指数函数y＝ax的值总大于，则实数a的取值范围是 ．
19．（2023•奉贤区校级三模）点P（2，16）、Q（lg23，t）都在同一个指数函数的图像上，则t＝ ．
20．（2023秋•奉贤区期中）若x＞0时，指数函数y＝（2a2﹣1）x的值总小于1，则实数a的取值范围为 ．
21．（2023秋•杨浦区校级期中）若指数函数的图像经过点，则指数函数的解析式为 ．
六．指数函数的图象与性质（共4小题）
22．（2023秋•普陀区校级期中）如图所示，函数y＝|2x﹣2|的图象是（ ）
A．B．
C．D．
23．（2023秋•静安区校级期中）若函数y＝（）|1﹣x|+m的图象与x轴有公共点，则m的取值范围是（ ）
A．m≤﹣1B．﹣1≤m＜0C．m≥1D．0＜m≤1
24．（2023秋•静安区校级期中）指数函数y＝ax（a＞0，a≠1）在区间[0，4]上的最大值与最小值之和为17，则a＝ ．
25．（2023秋•静安区期中）函数f（x）＝ax（a＞0且a≠1）在区间[1，2]上的最大值比最小值大，则a的值为 ．
七．指数型复合函数的性质及应用（共2小题）
26．（2020秋•黄浦区校级期末）函数f（x）＝x﹣3+ex的零点所在的区间是（ ）
A．（0，1）B．（1，3）C．（3，4）D．（4，+∞）
27．（2021秋•普陀区校级月考）已知函数f（x）＝（a∈R），且f（1）＞f（3），f（2）＞f（3）（ ）
A．若k＝1，则|a﹣1|＜|a﹣2|B．若k＝1，则|a﹣1|＞|a﹣2|
C．若k＝2，则|a﹣1|＜|a﹣2|D．若k＝2，则|a﹣1|＞|a﹣2|
八．指数函数的单调性与特殊点（共6小题）
28．（2023秋•静安区校级期中）函数f（x）＝ax+2﹣1（a＞0且a≠1）经过与a无关的定点 ．
29．（2023秋•青浦区校级期中）已知常数a＞0且a≠1，假设无论a为何值，函数y＝ax+4+3的图像恒经过一定点，则这个点的坐标为 ．
30．（2023秋•浦东新区校级期中）函数f（x）＝3x，x∈{1，2，3}的最小值为 ．
31．（2023秋•静安区校级期中）已知常数a＞0且a≠1，若无论a取何值，函数y＝ax﹣b+m（b，m为实数）的图象过定点（1，3），则b+m的值为 ．
32．（2023秋•普陀区校级期中）函数y＝ax﹣1（a＞0且a≠1）的图像一定过点 ．
33．（2023秋•杨浦区校级期中）已知a，b∈R，则下列命题中正确的个数为（ ）
（1）若0＜a＜b＜1，则aa＜bb； （2）若0＜a＜b＜1，则lgab＜1；
（3）若a＞b＞1，则ab＜ba； （4）若a＞b，则．
A．3个B．2个C．1个D．0个
九．指数函数的实际应用（共1小题）
34．（2022秋•徐汇区校级期末）某细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经过1小时，这种细菌由一个可以繁殖成 个．
一十．对数函数的定义域（共5小题）
35．（2023秋•虹口区期末）函数的定义域为 ．
36．（2023秋•宝山区校级期中）若lg（a﹣2）（5﹣a）有意义，则实数a的取值范围是 ．
37．（2023秋•宝山区校级期中）已知函数y＝lg（ax2+ax+1），若函数的定义域是R，则实数a的取值范围是 ．
38．（2023秋•徐汇区校级期中）若对于任意实数x，代数式均有意义，则实数a的取值范围是 ．
39．（2023秋•杨浦区校级期中）已知函数的定义域为集合A，集合B＝[a﹣2，a+2]．
（1）当a＝2时，求A∪B；
（2）若A⋂B＝B，求实数a的取值范围．
一十一．对数函数的值域与最值（共1小题）
40．（2022秋•杨浦区校级期中）已知函数f（x）＝lgax（0＜a＜1）在[2，4]上的最大值比最小值大2，则a的值为 ．
一十二．对数值大小的比较（共1小题）
41．（2022秋•徐汇区校级期末）如果a＞1，那么a0.7，0.7a，lg0.7a的大小顺序为（ ）
A． B．0.7a＜a0.7＜lg0.7a
C． D．
一十三．对数函数的图象与性质（共5小题）
42．（2023秋•杨浦区校级期中）有四个命题：①若a＞b，则a3＞b3；②若a＞b＞1，则lga2＞lgb2；③若a＜b＜0，c＜d＜0，则ac＞bd；④若1＜a＜2且0＜b＜3，则﹣2＜a﹣b＜2．其中真命题的是（ ）
A．①②③B．①②④C．①③④D．②③④
43．（2023秋•杨浦区校级期中）已知实数a满足0＜a＜1，则函数y＝lgax在[a3，a2]上的最大值是（ ）
A．3B．2C．D．
44．（2023秋•静安区校级期中）若f（x）＝lg（x2﹣2x+t）的值域为R，则t的取值范围是 ．
45．（2023秋•普陀区校级期中）已知函数f（x）＝lg2（x+a）．
（1）当a＝2时，解不等式：f（x）＜2lg2x；
（2）若函数y＝|f（x）|在x∈[﹣1，2]上的最大值为lg23，求a的值；
（3）当a＞0时，记，若对任意的x∈（0，2），函数y＝f（x）的图像总在函数y＝g（x）的图像的下方，求正数a的取值范围．
46．（2023秋•宝山区校级期中）已知两条水平直线l1：y＝m和l2：（其m＞0），且直线l1与函数y＝|lg2x|的图象从左至右相交于点A、B，直线l2与函数y＝|lg8x|的图象从左至右相交于点C、D．若记线段AC和BD在x轴上的投影长度分别为a、b（投影点重合时长度为0）．
（1）记点A、B、C、D的横坐标分别为xA、xB、xC、xD，求证：xAxB＝xCxD；
（2）当a＝b时，求m的值；
（3）当a≠0，m变化时，记，求函数y＝f（m）的解析式及其最小值．
一十四．对数函数的单调性与特殊点（共1小题）
47．（2022秋•金山区期末）已知常数a＞0且a≠1，无论a取何值，函数y＝lga（3x﹣5）﹣4的图像恒过一个定点，则此定点为 ．
一十五．指数函数与对数函数的关系（共1小题）
48．（2022秋•徐汇区校级期中）设2a＝5b＝m，且+＝2，m＝ ．
一十六．反函数（共3小题）
49．（2022秋•浦东新区校级期末）函数y＝x2﹣2x+3（x≤0）的反函数为 ．
50．（2022秋•徐汇区校级期末）定义在（0，+∞）上的函数y＝f（x）的反函数为y＝f﹣1（x），若为奇函数，则f﹣1（x）＝2的解为 ．
51．（2022秋•普陀区校级期末）设函数y＝x2+1（x≥0）的反函数为y＝f﹣1（x）．若f﹣1（a）＝2，则a＝ ．
一十七．对数函数图象与性质的综合应用（共1小题）
52．（2021秋•宝山区校级期末）已知函数f（x）＝a•2x﹣1+2﹣x（a为常数，x∈R）为偶函数．
（1）求a的值；并用定义证明f（x）在[0，+∞）上单调递增；
（2）解不等式：f（2lgax﹣1）＞f（lgax+1）．
一、填空题
1．函数的定义域为 .
2．一种专门侵占内存的计算机病毒，开机时占据内存，然后每2分钟自身又复制一次，复制后所占内存是原来的2倍，那么开机后经过 分钟，该病毒占据内存，其中.
3．函数（，且）在区间上的最大值比最小值大，则a的值为 ．
4．已知函数为幂函数且在第一象限为增函数，则m的值是 ．
5．若函数在区间上单调递减，则实数的取值范围是 ．
6．已知函数是幂函数，它的表达式为，且当时，是严格减函数，则的取值集合是 ．
7．当时，不等式恒成立，则实数的取值范围是 .
8．已知函数的图象过定点，函数也经过点，则的值为 ．
9．已知在上恒成立，则实数m的最小值是 ．
10．若是函数的反函数，且，则＝ ．
11．已知函数满足，当时，，且.若，则下列结论中正确的是 .（填写序号）
①；
②；
③可能为0；
④可正可负.
12．以下条件，①；②；③；④；⑤，；⑥，.能够使得：成立的有 .
二、单选题
13．函数的图象是（ ）
A．B．
C．D．
14．若，则的取值范围是：（ ）
A．B．或
C．D．或
15．已知幂函数在上是减函数，则的值为（ ）
A．1或B．1C．D．或3
16．在同一直角坐标系中，与的图象可能是（ ）
A． B．
C． D．
三、问答题
17．已知对数函数的图象经过点.
（1）求函数的解析式；
（2）如果不等式成立，求实数的取值范围.
18．已知函数是指数函数．
（1）求的表达式；
（2）令，解不等式：．
19．设函数．
（1）求函数的定义域
（2）若，求函数在区间上的最大值．
（3）解不等式：．
20．设是实数，函数的表达式为．
(1)当时，求满足的的取值范围；
(2)求函数的值域（用表示）．
21．已知函数的图象过点.
（1）当时，恒成立，求实数m的取值范围；
（2）若关于x的方程在上有解，求k的取值范围.
目录
考点聚焦：核心考点+高考考点，有的放矢
重点速记：知识点和关键点梳理，查漏补缺
难点强化：难点内容标注与讲解，能力提升
学以致用：真题感知+提升专练，全面突破
式子
名称
a
x
y
指数函数：y＝ax
底数
指数
幂值
幂函数：y＝xa
指数
底数
幂值
y＝x
y＝x2
y＝x3
y＝
y＝x﹣1
定义域
R
R
R
[0，+∞）
{x|x≠0}
值域
R
[0，+∞）
R
[0，+∞）
{y|y≠0}
奇偶性
奇
偶
奇
非奇非偶
奇
单调性
增
x∈[0，+∞）时，增
x∈（﹣∞，0]时，减
增
增
x∈（0，+∞）时，减
x∈（﹣∞，0）时，减
公共点
（1，1）（0，0）
（1，1）（0，0）
（1，1）（0，0）
（1，1）（0，0）
（1，1）
y＝ax
a＞1
0＜a＜1
图象
定义域
R
值域
（0，+∞）
性质
过定点（0，1）
当x＞0时，y＞1；
x＜0时，0＜y＜1
当x＞0时，0＜y＜1；
x＜0时，y＞1


在R上是增函数
在R上是减函数