【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题04+任意角的正弦、余弦、正切、余切（3大考点+4种题型）-练习.zip

这是一份【寒假作业】（沪教版2020）高中数学 高一寒假巩固提升训练 专题04+任意角的正弦、余弦、正切、余切（3大考点+4种题型）-练习.zip，文件包含寒假作业沪教版2020高中数学高一寒假巩固提升训练专题04任意角的正弦余弦正切余切3大考点+4种题型原卷版docx、寒假作业沪教版2020高中数学高一寒假巩固提升训练专题04任意角的正弦余弦正切余切3大考点+4种题型解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。

思维导图
核心考点聚焦
考点一、任意角的正弦、余弦、正切、余切
考点二、单位圆
考点三、同角三角关系
考点一、任意角的正弦、余弦、正切、余切
1. 任意角的正弦、余弦、正切、余切
我们将锐角置于平面直角坐标系中，锐角的顶点与原点重合，始边与轴的正半轴重合，那么它的终边在第一象限. 在角的终边上任取异于原点的一点，则点与原点的距离为
过P作x轴的垂线垂足为M，则线段OM的长度为x，线段MP的长度为y.
锐角的正弦、余弦、正切及余切的定义
，，
，.
这说明锐角的正弦、余弦、正切及余切可以用角的终边上点的坐标来定义. 这样，就可以对任意给定的角，定义其相应的正弦、余弦、正切及余切.
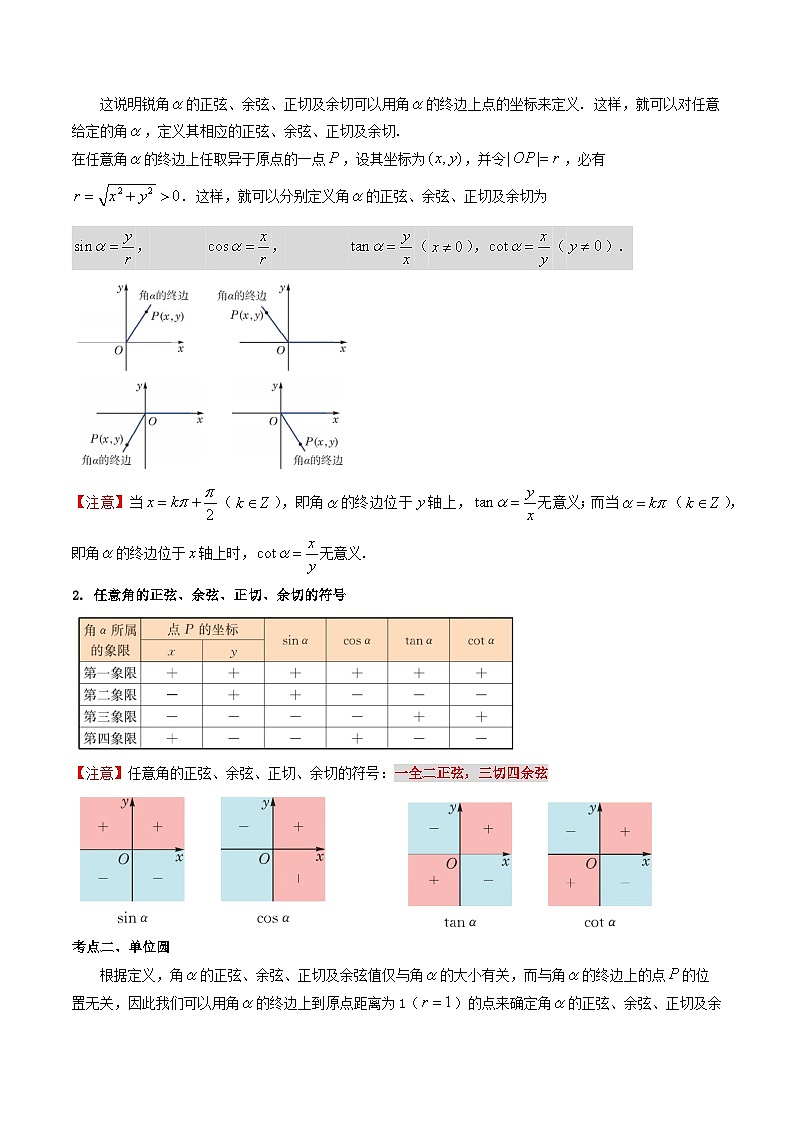
在任意角的终边上任取异于原点的一点，设其坐标为，并令，必有. 这样，就可以分别定义角的正弦、余弦、正切及余切为
， ， （），（）.
【注意】当（），即角的终边位于轴上，无意义；而当（），即角的终边位于轴上时，无意义.
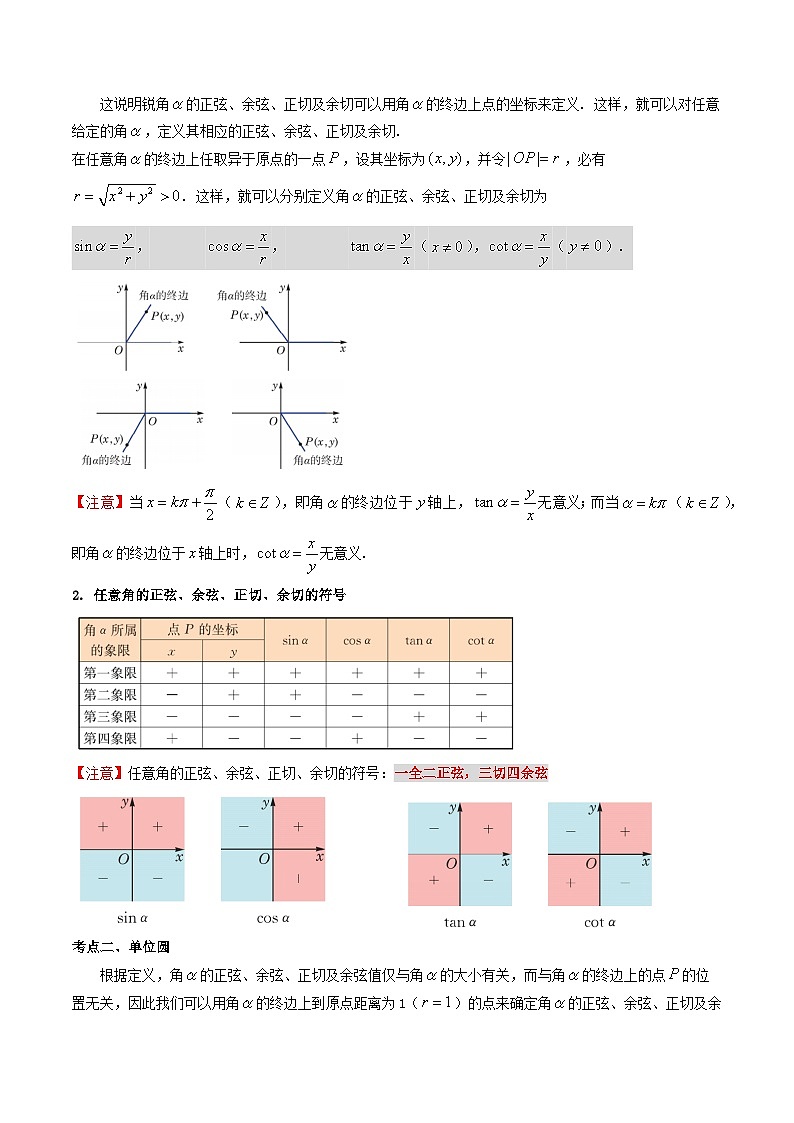
2. 任意角的正弦、余弦、正切、余切的符号
【注意】任意角的正弦、余弦、正切、余切的符号：一全二正弦，三切四余弦
考点二、单位圆
根据定义，角的正弦、余弦、正切及余弦值仅与角的大小有关，而与角的终边上的点的位置无关，因此我们可以用角的终边上到原点距离为1（）的点来确定角的正弦、余弦、正切及余切值.
半径为1个单位的圆称为单位圆. 本章中，如无特别说明，单位圆通常指在平面直角坐标系中以坐标原点为圆心，以1为半径的圆.
设角的终边与单位圆的交于唯一的一点，则根据定义可知，
，. 因此，单位圆上点的坐标必可以写为（）.
考点三、同角三角关系
设角的终边经过异于原点的一点，并记.
由定义，有，，（），（）.
由，就有 .
当时，有 .
当时，有 .
当、都有意义时，有 .
【注意】（1）“同角”的概念与角的表达形式无关，如：，.
（2）利用“平方关系”公式，最终需求平方根，会出现两解，应尽可能少用，若使用时，要注意讨论符号.
题型一：正弦、余弦、正切、余切的求解
【例1】（1）（2021春•宝山区校级试题）角的顶点与坐标原点重合，始边与轴的正半轴重合，其终边上有一点，则 ．
（2）（2021春•徐汇区校级试题）若角的始边落在轴正半轴，终边落在直线上，则 ．
（3）（2021春•徐汇区试题）已知角的终边上的一点，，则 ．
【答案】（1）；（2）；（3）
【解答】（1）则．
（2）由已知得，终边落在直线上，
所以，即，
再由 可得．
（3）因为角的终边上一点，，
又时，．
【变式1】（2021春•浦东新区校级试题）★☆☆☆☆
已知点在角的终边上，且，则 .
【答案】
【解答】解：因为点在角的终边上，且，可得，解得，解得．
【变式2】（2021春•金山区校级试题）
已知角的终边经过点，，则 ．
【答案】
【解答】解：角的终边过点，，
，，，
，，
．
故答案为：．
【变式3】（2020秋•徐汇区校级试题）★☆☆☆☆
若角终边过点，且，则等于 ．
【答案】3
【解答】解：角的终边经过点，
则，
又，
解得．
题型二：正弦、余弦、正切、余切的符号
【例2】（2021春•虹口区校级试题）已知点在第四象限，则角是第 象限角．
【答案】二
【解答】解：点在第四象限，
，且，
是第二象限角.
【变式1】已知是第三象限的角，则的符号是 号（填正或负）.
【答案】负
【解答】解：是第三象限的角，，，
则，，
即则，
故答案为：负．
【变式2】已知，则角所在的象限为 ．
【答案】三、四
【解答】解：可以转化为和异号，或者，由①得，为第四象限角，由②得，为第三象限角．故填：三、四
【变式3】函数的值域是 ．
【答案】，，
【解答】解：由题意可知不在坐标轴上，
当为第一象限角时，函数；
当为第二象限角时，函数；
当为第三象限角时，函数；
当为第四象限角时，函数．
函数的值域是数集，，．
故答案为：，，．
题型三：单位圆
【例3】求的正弦、余弦和正切值.
【解析】如图，在中，，
，，进而
【变式】、若角α的终边与单位圆相交于点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)，－\f(\r(2),2)))，则sin α的值为
【答案】－eq \f(\r(2),2)；
【解析】利用任意角三角函数的定义可知，点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)，－\f(\r(2),2)))到原点的距离为1，则sin α＝eq \f(－\f(\r(2),2),1)＝－eq \f(\r(2),2)；
【考点】任意角的三角比、单位圆；注意：利用单位圆简化计算；
题型四：同角三角函数
【例4】已知，且为第二象限的角，求，及.
【解析】为第二象限的角，. 由，得，
从而，.
【变式1】已知，求、及.
【解析】. ，为第二象限或第四象限的角.
，. 又，解方程组，得
，，或，.
于是，当为第二象限的角时，，；
而当为第四象限的角时，，.
【变式2】已知，求下列各式的值：（1）； （2）.
【答案】（1）；（2）
【解析】（1）
（2）
【小结】（1）齐一次，分子分母同除；（2）齐二次，分子分母同除
一、填空题
1、如果角α的终边过点P(2sin30°，－2cs30°)，则sinα的值等于
【答案】－eq \f(\r(3),2)；
【解析】由题意得P(1，－eq \r(3))，它与原点的距离r＝eq \r(12＋－\r(3)2)＝2，所以sinα＝－eq \f(\r(3),2)；
2、设角α的终边上有一点P(4，－3)，则2sin α＋cs α的值是
【答案】－eq \f(2,5)；
【解析】由三角函数的定义可知sin α＝eq \f(－3,\r(42＋（－3）2))＝－eq \f(3,5)，cs α＝eq \f(4,\r(42＋（－3）2))＝eq \f(4,5)，
所以2sin α＋cs α＝2×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,5)))＋eq \f(4,5)＝－eq \f(2,5)；
3、已知P(－2，y)是角α终边上一点，且sin α＝－eq \f(\r(5),5)，则cs α＝________
【答案】－eq \f(2\r(5),5)；
【解析】因为r＝eq \r(4＋y2)，所以sin α＝eq \f(y,r)＝eq \f(y,\r(y2＋4))＝－eq \f(\r(5),5)，所以y<0，所以y＝－1，r＝eq \r(5)，
所以cs α＝eq \f(x,r)＝eq \f(－2,\r(5))＝－eq \f(2\r(5),5)；
【考点】任意角α的三角比的定义；求任意角的三角函数值的两种方法
第一步，根据定义，在角α的终边上任取一点P(x，y)(P与原点O不重合)；
第二步，计算r：r＝|OP|＝eq \r(x2＋y2)(r>0)；
第三步，求值：由sin α＝eq \f(y,r)，cs α＝eq \f(x,r)求值
4、当α为第四象限时，eq \f(|sin α|,sin α)－eq \f(|cs α|,cs α)的值是____________．
【答案】－2；
【解析】因为α为第四象限角，所以eq \f(|sin α|,sin α)＝－1，eq \f(|cs α|,cs α)＝1.所以eq \f(|sin α|,sin α)－eq \f(|cs α|,cs α)＝－1－1＝－2；
5、若三角形的两内角α，β满足sin α·cs β<0，则此三角形必为 三角形。
【答案】钝角；
【解析】三角形的两内角α，β的终边一定落在第一、二象限或y轴正半轴上，sin α·cs β <0，所以sin α>0，cs β <0，所以角β为钝角，此三角形为钝角三角形；
6、已知角α的终边上有一点Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(5),5)，－\f(2\r(5),5)))，则sinα＋csα＝________.
【答案】－eq \f(\r(5),5)；
【解析】结合三角比的定义与单位圆；sinα＋csα＝－2×eq \f(\r(5),5)+eq \f(\r(5),5)=－eq \f(\r(5),5)；
7、若sin α<0，tan α>0，则α在第__________象限．
【答案】三；
【考点】三角比的符号；尝试：利用三角比的定义解答，
8、若角α的终边上有一点P(－4，a)，且sin α·cs α＝eq \f(\r(3),4)，则a＝________.
【答案】－4eq \r(3)或－eq \f(4\r(3),3)；
【解析】因为点P(－4，a)且sin α·cs α＝eq \f(\r(3),4)，所以a<0，根据定义可得eq \f(a,\r(a2＋16))·eq \f(－4,\r(a2＋16))＝eq \f(\r(3),4)，
解得a＝－4eq \r(3)或－eq \f(4\r(3),3)；
9、若sinα=，且α为第四象限角，则tanα的值等于
【答案】；
【解析】由sinα=-，且α为第四象限角可知csα=，故；
10、若，则的值是
【答案】2；
【解析】；
11、已知sin α＋cs α＝eq \f(7,13)，α∈(0，π)，则tan α＝
【答案】－eq \f(12,5)；
【解析】因为，sin α＋cs α＝eq \f(7,13)，所以，(sin α＋cs α)2＝eq \f(49,169)，即2sin αcs α＝－eq \f(120,169)<0，
又α∈(0，π)，则sin α>0，cs α<0，∴α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，
故sin α－cs α＝eq \r(sin α＋cs α2－4sin αcs α)＝eq \f(17,13)，
可得sin α＝eq \f(12,13)，cs α＝－eq \f(5,13)，tan α＝－eq \f(12,5).
12. 如果满足条件 ，则所在象限是________.
【答案】二、四
【提示】（四）或（二）
二、选择题
13、已知角α的终边过点P(－1，2)，则cs α的值为( )
A．－eq \f(\r(5),5) B．－eq \r(5) C．eq \f(2\r(5),5) D．eq \f(\r(5),2)
【答案】A；
【解析】由题意得：r＝eq \r(－12＋22)＝eq \r(5)，cs α＝eq \f(x,r)＝－eq \f(\r(5),5)；
14、已知sin α＝eq \f(3,5)，cs α＝－eq \f(4,5)，则角α所在的象限是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B；
【解析】由sin α>0得角α的终边在第一或第二象限；由cs α<0得角α的终边在第二或第三象限．综上，角α所在的象限是第二象限；
15、若a＝sin 2，b＝cs 2，则a，b的大小关系为( )
A．a【答案】B；
【解析】因为eq \f(π,2)<2<π，作出2的正弦线，余弦线．显然sin 2>cs 2.
16、函数y＝eq \r(sin x)＋eq \r(－cs x)的定义域是（ ）
A．(2kπ，2kπ＋π)，k∈Z[来 B. eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(π,2)，2kπ＋π))，k∈Z
C. eq \b\lc\[\rc\](\a\vs4\al\c1(kπ＋\f(π,2)，kπ＋π))，k∈Z D．[2kπ，2kπ＋π]，k∈Z
【答案】B；
【解析】由sin x≥0，－cs x≥0，得x为第二象限角或y轴正半轴上的角或x轴负半轴上的角，
所以2kπ＋eq \f(π,2)≤x≤2kπ＋π，k∈Z；
三、解答题
17、已知角θ的终边上有一点P(x，3)(x≠0)，且cs θ＝eq \f(\r(10),10)x，求：sin θ＋tan θ的值
【答案】eq \f(3\r(10)＋30,10)或eq \f(3\r(10)－30,10)；
【解析】因为r＝ eq \r(x2＋9)，cs θ＝eq \f(x,r)，所以eq \f(\r(10),10)x＝eq \f(x,\r(x2＋9)) ；
又x≠0，所以x＝±1，所以r＝eq \r(10).又y＝3>0，所以θ是第一或第二象限角．
当θ为第一象限角时，sin θ＝eq \f(3\r(10),10)，tan θ＝3；则sin θ＋tan θ＝eq \f(3\r(10)＋30,10).
当θ为第二象限角时，sin θ＝eq \f(3\r(10),10)，tan θ＝－3.则sin θ＋tan θ＝eq \f(3\r(10)－30,10).
18、角θ的终边落在直线y＝2x上，求sin θ，cs θ的值.
【解析】①若θ的终边在第一象限内，设点P(a，2a)(a>0)是其终边上任意一点，
因为r＝|OP|＝eq \r(a2＋4a2)＝eq \r(5)a，所以sin θ＝eq \f(y,r)＝eq \f(2a,\r(5)a)＝eq \f(2\r(5),5)，cs θ＝eq \f(x,r)＝eq \f(a,\r(5)a)＝eq \f(\r(5),5).
②若θ的终边在第三象限内，设点P(a,2a)(a<0)是其终边上任意一点，
因为r＝|OP|＝eq \r(a2＋4a2)＝－eq \r(5)a(a<0)，
所以sin θ＝eq \f(y,r)＝eq \f(2a,－\r(5)a)＝－eq \f(2\r(5),5)，cs θ＝eq \f(x,r)＝eq \f(a,－\r(5)a)＝－eq \f(\r(5),5).
19、已知tan α＝2，求下列代数式的值：（1）eq \f(4sin α－2cs α,5cs α＋3sin α)；（2）eq \f(1,4)sin2α＋eq \f(1,3)sin αcs α＋eq \f(1,2)cs2α；
【解析】（1）原式＝eq \f(4tan α－2,5＋3tan α)＝eq \f(6,11)；
（2）原式＝eq \f(\f(1,4)sin2α＋\f(1,3)sin αcs α＋\f(1,2)cs2α,sin2α＋cs2α)＝eq \f(\f(1,4)tan2α＋\f(1,3)tan α＋\f(1,2),tan2α＋1)＝eq \f(\f(1,4)×4＋\f(1,3)×2＋\f(1,2),5)＝eq \f(13,30).
20. 已知，求：
（1）的值；
（2）的值.
【解析】（1）；
（2）
21. 设、是方程的两根，求m与的值.
【答案】；
【解析】