专题7.2 非线性回归问题（3类必考点）-2023-2024学年高二数学必考考点各个击破（北师大版选择性必修第一册）

这是一份专题7.2 非线性回归问题（3类必考点）-2023-2024学年高二数学必考考点各个击破（北师大版选择性必修第一册），文件包含专题72非线性回归问题3类必考点北师大版选择性必修第一册原卷版docx、专题72非线性回归问题3类必考点北师大版选择性必修第一册解析版docx等2份试卷配套教学资源，其中试卷共51页， 欢迎下载使用。

TOC \ "1-3" \t "正文,1" \h
\l "_Tc18139" 【考点1：非线性回归类型一：幂函数型】 PAGEREF _Tc18139 \h 1
\l "_Tc3372" 【考点2：非线性回归类型二：指数函数型】 PAGEREF _Tc3372 \h 10
\l "_Tc20956" 【考点3：非线性回归类型三：对数函数型】 PAGEREF _Tc20956 \h 17
【知识要点】
1、建立非线性回归模型的基本步骤：
①确定研究对象，明确哪个是解释变量，哪个是预报变量；
②画出确定好的解释变量和预报变量的散点图，观察它们之间的关系（是否存在非线性关系）；
③由经验确定非线性回归方程的类型（如我们观察到数据呈非线性关系，一般选用反比例函数、指数函数、对数函数模型等）；
④通过换元，将非线性回归方程模型转化为线性回归方程模型；
⑤按照公式计算线性回归方程中的参数（如最小二乘法），得到线性回归方程；
⑥消去新元，得到非线性回归方程；
⑦得出结果后分析残差图是否有异常.若存在异常，则检查数据是否有误，或模型是否合适等.
常见的非线性回归方程的转化：
【考点1：非线性回归类型一：幂函数型】
【知识点：类型一：幂函数型】
1．（2023·高二课时练习）2020年初，新型冠状病毒（COVID-19）引起的肺炎疫情爆发以来，各地医疗机构采取了各种针对性的治疗方法，取得了不错的成效，某地开始使用中西医结合方法后，每周治愈的患者人数如下表所示：由表格可得y关于x的二次回归方程为y=6x2+a，则此回归模型第4周的残差（实际值与预报值之差）为（ ）
A．0B．1C．4D．5
【答案】D
【分析】令t=x2，则y关于t的一次回归方程为y=6t+a，求出t,y，根据线性回归方程过样本中心点求出a，从而可求得预测值，即可得出残差.
【详解】令t=x2，则y关于t的一次回归方程为y=6t+a，
t=1+4+9+16+255=11,y=2+17+36+93+1425=58，
则58=6×11+a，解得a=−8，
则y=6x2−8，
令x=4，得y=6×16=8=88，
所以残差为93−88=5.
故选：D.
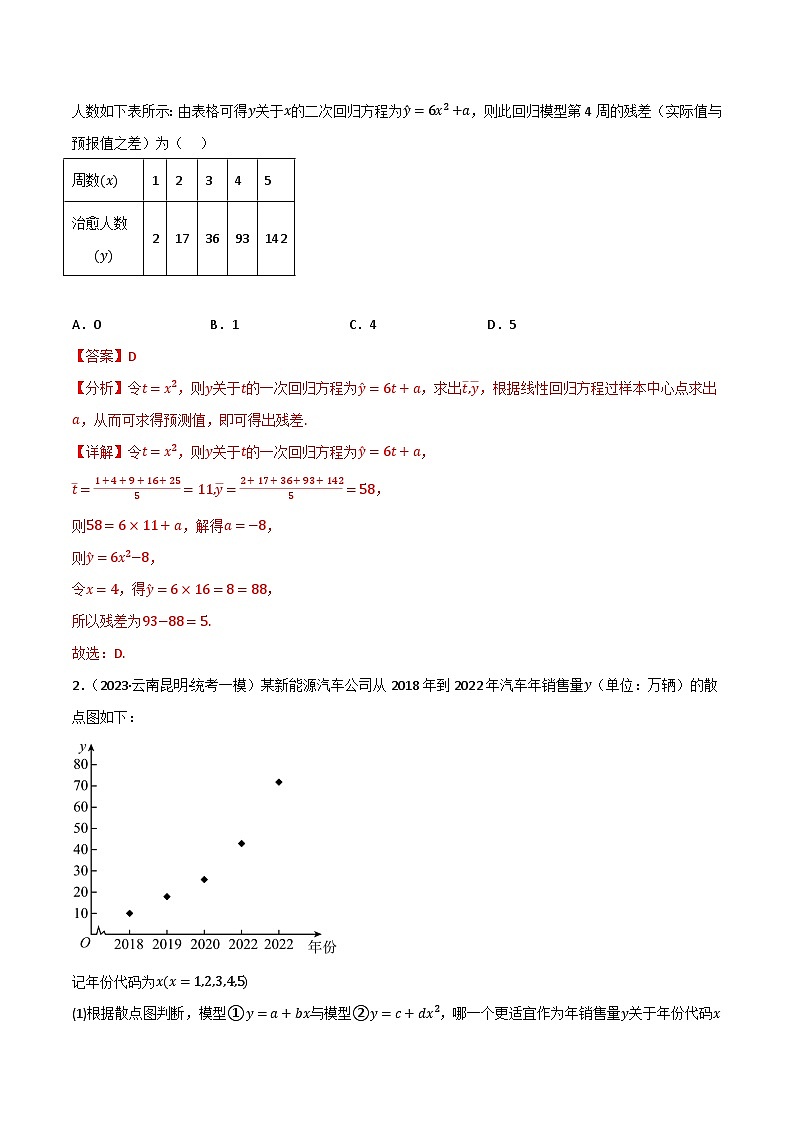
2．（2023·云南昆明·统考一模）某新能源汽车公司从2018年到2022年汽车年销售量y（单位：万辆）的散点图如下：
记年份代码为xx=1,2,3,4,5
(1)根据散点图判断，模型①y=a+bx与模型②y=c+dx2，哪一个更适宜作为年销售量y关于年份代码x的回归方程？（给出判断即可，不必说明理由）
(2)根据（1）的判断结果，建立y关于x的回归方程；
(3)预测2023年该公司新能源汽车销售量．
参考数据：
参考公式：回归方程y=a+bx中斜率和截距的最小二乘估计公式分别为：b=i=1nxi−xyi−yi=1nxi−x2=i=1nxiyi−nx⋅yi=1nxi2−nx2，a=y−bx
【答案】(1)y=c+dx2
(2)y=6.5+2.5x2
(3)预测2023年该公司新能源汽车销售量96.5万辆
【分析】（1）根据散点图结合一次函数、二次函数的图象特征分析判断；
（2）换元令t=x2，结合题中数据与公式运算求解；
（3）令x=6，代入回归方程运算求解.
【详解】（1）由散点图可知：散点图与一次函数偏差较大，与二次函数较接近，故模型②y=c+dx2更适合.
（2）令t=x2，则i=15ti2=i=15xi4=979,i=15tiyi=i=15xi2yi=2805,t=15i=15ti=15i=15xi2=11，y=34，
对于回归方程y=c+dt，
可得：d=i=15tiyi−5t⋅yi=15ti2−5t2=2805−5×11×34979−5×112=935374=2.5，c=y−dt=34−2.5×11=6.5，
故回归方程为y=6.5+2.5t，即y=6.5+2.5x2.
（3）由（2）可得：y=6.5+2.5x2，
令x=6，则y=6.5+2.5×62=96.5，
预测2023年该公司新能源汽车销售量96.5万辆.
3．（2023·全国·高二专题练习）某电商平台统计了近七年小家电的年度广告费支出xi(万元)与年度销售量yi(万台)的数据，如表所示:
其中i=17xiyi=279.4，i=17xi2=708
(1)若用线性回归模型拟合y与x的关系，求出y关于x的线性回归方程；
(2)若用y=c+dx模型拟合得到的回归方程为y=1.63+0.99x，经计算线性回归模型及该模型的R2分别为0.75和0.88，请根据R2的数值选择更好的回归模型拟合y与x的关系，进而计算出年度广告费x为何值时，利润z=200y−x的预报值最大？
参考公式：b=i=1nxiyi−nxyi=1nxi2−nx2=i=1nxi−xyi−yi=1nxi−x2，a=y−bx；
【答案】(1)y=0.17x+2.84
(2)选用回归方程y=1.63+0.99x更好，x=9801时，利润的预报值最大
【分析】(1)根据数据，利用公式即可求出线性回归方程；
（2）R2越大拟合效果越好，选用回归方程y=1.63+0.99x更好，从而计算出结果.
【详解】（1）由题意可得：
x=1+2+4+6+11+13+197=8
y=1.9+3.2+4.0+4.4+5.2+5.3+5.47=4.2
所以b=i=17xiyi−7xyi=17xi2−7x2=279.4−7×8×4.2708−7×82=0.17，
a=y−bx=4.2−0.17×8=2.84，
y关于x的线性回归方程：y=0.17x+2.84.
（2）因为0.75<0.88，R2越大拟合效果越好，
选用回归方程y=1.63+0.99x更好，
z=2001.63+0.99x−x=−x+198x+326
z=−x−992+10127，
即当x=99时，x=9801时，利润的预报值.
4．（2023·全国·高二专题练习）某公司为了解年营销费用x（单位：万元）对年销售量y（单位：万件）的影响，统计了近5年的年营销费用xi和年销售量yi(i=1,2,3,4,5)，得到的散点图如图所示，对数据进行初步处理后，得到一些统计量的值如下表所示．
表中ui=lnxi，vi=lnyi，u=15i=15ui，v=15i=15vi．已知y=a⋅xb可以作为年销售量y关于年营销费用x的回归方程．
(1)求y关于x的回归方程；
(2)若公司每件产品的销售利润为4元，固定成本为每年120万元，用所求的回归方程估计该公司每年投入多少营销费用，才能使得该产品一年的收益达到最大？（收益=销售利润−营销费用−固定成本）
参考数据：e4.399≈81，33≈139．
参考公式：对于一组数据u1,v1,u2,v2,⋯,un,vn，其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=i=1nui−uvi−v`i=1nui−u2，α=v−βu．
【答案】(1)y=81x14
(2)该公司每年投入351万元营销费用时，该产品一年的收益达到最大
【分析】(1)根据题目要求可知，y关于x的回归方程为非线性的，设y=a⋅xb，可得lny=lna+blnx，代入已知条件所给的数据，计算即可.(2)列出年收益与营销费用的关系式，通过求导来求得最值.
【详解】（1）由y=a⋅xb得，lny=ln(a⋅xb)=lna+blnx，令u=lnx，v=lny，c=lna，则v=c+bu．
由表中数据可得，b=i=15ui−uvi−vi=15ui−u2=，
则c=v−bu=26.025−0.25×16.15=4.399，所以v=4.399+0.25u．
即lny=4.399+0.25lnx =lne4.399⋅x14，因为e4.399≈81，所以y=81x14，
故所求的回归方程为y=81x14．
（2）设年收益为W万元，则W=4y−x−120=324x14−x−120，
对W=f(x)求导，得f'(x)=81x−34−1，
令81x−34−1=0，解得x=24333≈243×139=351，
当x∈(0,351)时，f'(x)>0，f(x)单调递增，当x∈(351,+∞)时，f'(x)<0，f(x)单调递减，
因此，当x=351时W有最大值，即该公司每年投入351万元营销费用时，该产品一年的收益达到最大．
5．（2023春·高二单元测试）某企业为改进生产，现 某产品及成本相关数据进行统计．现收集了该产品的成本费y（单位：万元/吨）及同批次产品生产数量x（单位：吨）的20组数据．现分别用两种模型①y=bx+a，②y=dx+c进行拟合，据收集到的数据，计算得到如下值：
表中ti=1xi，t=120i=120ti．
若用R2=1−i=1nyi−y2i=1nyi−y2刻画回归效果，得到模型①、②的R2值分别为R12=0.7891，R22=0.9485．
(1)利用R12和R22比较模型①、②的拟合效果，应选择哪个模型？并说明理由；
(2)根据（1）中所选择的模型，求y关于x的回归方程；并求同批次产品生产数量为25（吨）时y的预报值．
附：对于一组数据x1,y1，x2,y2，…，xn,yn，其回归直线y=a+βx的斜率和截距的最小二乘法估计分别为β=i=1nxi−xyi−yi=1nxi−x2，a=y−βx．
【答案】(1)选择模型②，理由见解析；
(2)6.
【分析】（1）根据已知R22>R12，根据R2的意义，即可得出模型②的拟合效果好，选择模型②；
（2）y与t可用线性回归来拟合，有y=dt+c，求出系数d,c，得到回归方程y=100t+2，即可得到成本费y与同批次产品生产数量x的回归方程为y=100x+2，代入x=25，即可求出结果.
【详解】（1）应该选择模型②.
由题意可知，R22>R12，则模型②中样本数据的残差平方和i=1nyi−y2比模型①中样本数据的残差平方和小，即模型②拟合效果好.
（2）由已知t=1x，成本费y与t可用线性回归来拟合，有y=dt+c.
由已知可得，d^=i=120(yi−y)(ti−t)i=120(ti−t)2=40.04=100，
所以c=y−dt=10−100×0.08=2，
则y关于t的线性回归方程为y=100t+2.
成本费y与同批次产品生产数量x的回归方程为y=100x+2，
当x=25（吨）时，y=10025+2=6（万元/吨）.
所以，同批次产品生产数量为25（吨）时y的预报值为6万元/吨.
6．（2023·江苏·高二专题练习）有一个开房门的游戏，其玩法为:
盒中先放入两把钥匙T和两把钥匙F，T能够打开房门，F不能打开房门.
每次从盒中随机取一把试开，试开后不放回钥匙.第一次打开房门后，关上门继续试开，第二次打开房门后停止抽取，称为进行了一轮游戏.
若每一轮取钥匙不超过三次，则该轮“成功”，否则为“失败”，如果某一轮“成功”，则游戏终止；若“失败”，则将所有钥匙重新放入盒中，并再放入一把钥匙F，继续下一轮抽取，直至“成功”.
(1)有1000名爱好者独立参与这个游戏，记t表示“成功”时抽取钥匙的轮次数，y表示对应的人数，部分统计数据如下表:
若将y=bt2+a作为y关于t的经验回归方程，估计抽取7轮才“成功”的人数（人数精确到个位）；
(2)由于时间关系，规定：进行游戏时，最多进行三轮，若均未“成功”也要终止游戏.求游戏要进行三轮的概率.
参考公式：最小二乘估计b=i=1nxiyi−nxyi=1nxi2−nx2，a=y−bx.
参考数据：取i=15xi2=1.08，x=0.3，其中xi=1ti2，x=15i=15xi.
【答案】(1)14人
(2)720
【分析】（1）利用参考数据以及最小二乘法公式求出b、a的值，可得出经验回归方程，然后在回归方程中令t=7，可求得结果；
（2）设事件A为“第一轮成功”，事件B为“第二轮成功”，则A、B相互独立，分析可知游戏要进行三轮，即前两轮均失败，计算出PA、PB的值，利用对立事件和独立事件的概率公式可求得所求事件的概率.
【详解】（1）解：令xi=1ti2，设y=bx+a，
由条件知i=15xiyi=507+1444+729+3216+2525=554，y=507+144+72+32+255=156，
所以b=i=15xiyi−5xyi=15xi2−5x2=554−5×0.3×1561.08−5×0.32=3200.63≈507.94，
a=156−507.94×0.3=3.618，从而y=507.94x+3.618，
故所求的回归方程为y=507.94t2+3.618.
所以，估计当t=7时，y=507.9449+3.618≈14，即抽取7轮才“成功”的人数约为14人.
（2）解：由条件知，游戏要进行三轮，即前两轮均失败.
设事件A为“第一轮成功”，事件B为“第二轮成功”，则A、B相互独立.
因为PA=A22A42+C21C21A22A43=12，PB=A22A52+C21C31A22A53=310，
所以，前两轮均失败的概率为PAB=PAPB=12×710=720.
故游戏要进行三轮的概率为720.
7．（2023春·高二单元测试）根据党的“扶贫同扶志、扶智相结合”精准扶贫、精准脱贫政策，中国儿童少年基金会为了丰富留守儿童的课余文化生活，培养良好的阅读习惯，在农村留守儿童聚居地区捐建“小候鸟爱心图书角”.2016年某村在寒假和暑假组织开展“小候鸟爱心图书角读书活动”，号召全村少年儿童积极读书，养成良好的阅读习惯，下表是对2016年以来近5年该村庄100位少年儿童的假期周人均读书时间的统计：
现要建立y关于x的回归方程，有两个不同回归模型可以选择，模型一:y=bx+a；模型二:y=cx2+d，即使画出y关于x的散点图，也无法确定哪个模型拟合效果更好，现用最小二乘法原理，已经求得模型一的方程为y=3.1x−2.8.
(1)请你用最小二乘法原理，结合下面的参考数据及参考公式求出模型二的方程（计算结果保留到小数点后一位）；
(2)用计算残差平方和的方法比较哪个模型拟合效果更好，已经计算出模型一的残差平方和为i=15y1−y12=3.7.
附：参考数据：i=15tiyi−5tyi=15ti2−5t2≈0.52，其中ti=xi2，i=1,2,3,4,5.
参考公式：对于一组数据u1,v1，u2,v2，…，un,vn，其回归直线v=a−βu的斜率和截距的最小二乘法估计公式分别为β=i=1nuivi−nuvi=1nui2−nu2，a=v−βu.
【答案】(1)y=0.5x2+0.8；
(2)模型二的拟合效果更好.
【分析】（1）首先换元令t=x2，先求得t和y，再根据数据和参考公式求得模型二的方程；
（2）利用残差公式，求模型二的残差，比较大小，即可判断.
【详解】（1）令t=x2，则模型二可化为y关于t的线性回归问题，则
t=1+4+9+16+255=11，y=1.3+2.8+5.7+8.9+13.85=6.5，
则由参考数据可得c=i=15tiyi−5tyi=15ti2−5t2≈0.52≈0.5，
d=y−ct=6.5−0.52×11≈0.8，
则模型二的方程为y=0.5x2+0.8；
（2）由模型二的回归方程可得，y12=0.5×1+0.8=1.3，
y2(2)=0.5×4+0.8=2.8，y3(2)=0.5×9+0.8=5.3，y4(2)=0.5×16+0.8=8.8，
y5(2)=0.5×25+0.8=13.3，
∴i=15yi−yi(2)2=02+02+0.42+0.12+0.52=0.42<3.7，
故模型二的拟合效果更好.
【考点2：非线性回归类型二：指数函数型】
【知识点：类型二：指数函数型】
1．（2023·高二课时练习）以模型y=cekx(c>0)去拟合一组数据时，为了求出回归方程，设z=lny，将其变换后得到经验回归方程z=2x−1，则k,c的值分别是（ ）
A．−2,eB．2,1eC．−2,1eD．2,e
【答案】B
【分析】模型y=cekx(c>0)两边取对数，又z=lny，可得z=lnc+kx，又已知回归方程z=2x−1，可求k,c的值.
【详解】由题意得lny=lncekx=lnc+kx，设z=lny，可得z=lnc+kx.
又经验回归方程为z=2x−1，
所以lnc=−1,k=2，故c=1e,k=2.
故选：B
2．（2023·广东梅州·统考二模）云计算是信息技术发展的集中体现，近年来，我国云计算市场规模持续增长.已知某科技公司2018年至2022年云计算市场规模数据，且市场规模y与年份代码x的关系可以用模型y=c1ec2x（其中e为自然对数的底数）拟合，设z=lny，得到数据统计表如下：
由上表可得经验回归方程z=0.52x+a，则2025年该科技公司云计算市场规模y的估计值为（ ）
A．e5.08B．e5.6C．e6.12D．e6.5
【答案】B
【分析】根据a=z−bx可得线性回归方程，再由回归方程求出2025年z的预测值，代入z=lny即可得解.
【详解】因为x=3,z=3，
所以a=z−0.52x=3−3×0.52=1.44，
即经验回归方程z=0.52x+1.44，
当x=8时，z=0.52×8+1.44=5.6，
所以y=ez=e5.6，
即2025年该科技公司云计算市场规模y的估计值为e5.6，
故选：B
3．（2023春·湖南张家界·高二慈利县第一中学校考期中）对具有相关关系的两个变量x和y进行回归分析时，经过随机抽样获得成对的样本点数据xi,yii=1,2,⋯,n，则下列结论正确的是（ ）
A．若两变量x，y具有线性相关关系，则回归直线至少经过一个样本点
B．若两变量x，y具有线性相关关系，则回归直线一定经过样本点中心(x,y)
C．若以模型y=aeℎx(a>0)拟合该组数据，为了求出回归方程，设z=lny，将其变换后得到线性方程z=6x+ln3，则a，h的估计值分别是3和6
D．回归分析中常用残差平方和来刻画拟合效果好坏，残差平方和越小，拟合效果越好
【答案】BCD
【分析】根据回归方程的性质判断A，B，比较列方程确定a，h的估计值判断C，根据残差和的意义判断D.
【详解】对于A，若两变量x，y具有线性相关关系，则所有样本点都可能不在回归直线上，A错误；
对于B，若两变量x，y具有线性相关关系，则回归直线一定经过样本点中心(x,y)，B正确；
对于C，因为y=aeℎx(a>0)，所以lny=ℎx+lna，即z=ℎx+lna，又z=6x+ln3，所以a，h的估计值分别是3和6，C正确；
对于D，残差平方和越小，拟合效果越好，D正确；
故选：BCD.
4．（2023·全国·模拟预测）为了研究某种细菌随天数x变化的繁殖个数y，收集数据如下：
(1)在图中作出繁殖个数y关于天数x变化的散点图，并由散点图判断y=bx+a（a，b为常数）与y=c1ec2x（c1，c2为常数，且c1>0，c2≠0）哪一个适宜作为繁殖个数y关于天数x变化的回归方程类型？（给出判断即可，不必说明理由）
(2)对于非线性回归方程y=c1ec2x（c1，c2为常数，且c1>0，c2≠0），令z=lny，可以得到繁殖个数的对数z关于天数x具有线性关系及一些统计量的值．
①证明：“对于非线性回归方程y=c1ec2x，令z=lny，可以得到繁殖个数的对数z关于天数x具有线性关系（即z=βx+α，β，α为常数）”；
②根据（1）的判断结果及表中数据，建立y关于x的回归方程（系数保留2位小数）．
附：对于一组数据u1,v1，u2,v2，…，un,vn，其回归直线方程v=βu+α的斜率和截距的最小二乘估计分别为β=i=1nui−uvi−vi=1nui−u2，α=v−βu．
【答案】(1)作图见解析，选择y=c1ec2x为回归方程较适宜
(2)① 证明见解析；②y=e0.69x+1.12
【分析】（1）根据散点图，结合一次函数和指数型函数图象的特征进行判断即可；
（2）①根据对数与指数的互化公式进行求解即可；
②利用题中所给的数据和公式进行求解即可.
【详解】（1）作出散点图如图所示．
由散点图看出样本点分布在一条指数型曲线的周围，
故选择y=c1ec2x为回归方程较适宜；
（2）①由已知，z=lny，则z=lny=lnc1ec2x=lnc1+lnec2x=lnc1+c2x，
则α=lnc1，β=c2，即z=βx+α．所以繁殖个数的对数z关于天数x具有线性关系．
②由①知繁殖个数的对数z关于天数x可以用线性回归方程来拟合．
由表中数据可得β=i=16xi−xyi−yi=16xi−x2=12.0917.5≈0.69，
α=z=βx=3.53−0.69×3.5≈1.12，
则z关于x的线性回归方程为z=0.69x+1.12．
又z=lny，
因此细菌的繁殖个数y关于天数x的非线性回归方程为y=e0.69x+1.12．
5．（2023春·四川成都·高二树德中学校考阶段练习）某高科技公司对其产品研发年投资额x（单位：百万元）与其年销售量y（单位：千件）的数据进行统计，整理后得到如下统计表1和散点图.通过初步分析，求得年销售量y关于年投资额x的线性回归方程为y=1.2x−1.3.
(1)该公司科研团队通过进一步分析散点图的特征后，计划用y=ebx+a作为年销售量y关于年投资额x的非线性回归方程，请根据参考数据及表2的数据，求出此方程；
(2)若求得线性回归模型的相关系数R12=0.88，请根据参考数据，求出（1）中非线性回归模型的相关系数R22，并比较两种回归方程的拟合效果哪个更好？（精确到0.01）
参考数据：i=15xi2=55，i=15xizi=13.4；e−0.68≈0.54，e−0.09≈0.96，e0.50≈1.74，e1.09≈3.15，e1.68≈5.67；
参考公式：b=i=1nxi−xyi−yi=1nxi−x2=i=1nxiyi−nxyi=1nxi2−nx2，a=y−bx，R2=1−i=1nyi−yi2i=1nyi−y2=1−i=1nyi−yi2i=1nyi2−ny2.
【答案】(1)y=e0.59x−1.27
(2)0.99，非线性回归方程拟合效果更好
【分析】（1）根据已知公式计算b，a，根据z=lny，即可求得答案；
（2）由（1）的结论y=e0.59x−1.27，求得R22，与R12=0.88相比较，可得结论.
【详解】（1）由y=ebx+a，则lny=bx+a，记z=lny，即z=bx+a，
z=−0.7+0+0.4+1.1+1.75=0.5，x=1+2+3+4+55=3，
b=13.4−5×3×0.555−5×32=0.59，a=0.5−0.59×3=−1.27，
所以z=lny=0.59x−1.27，即非线性回归方程为y=e0.59x−1.27.
（2）由（1）可得：y=e0.59x−1.27，
R22≈1−−0.042+0.042+−0.242+−0.152+−+12+1.52+32+5.52−5×2.32≈0.99，
显然R22>R12=0.88，故非线性回归方程拟合效果更好.
6．（2023·广东江门·统考一模）某高科技公司对其产品研发年投资额x（单位：百万元）与其年销售量y（单位：千件）的数据进行统计，整理后得到如下统计表和散点图.
(1)该公司科研团队通过分析散点图的特征后，计划分别用①y=bx+a和②y=edx+c两种方案作为年销售量y关于年投资额x的回归分析模型，请根据统计表的数据，确定方案①和②的经验回归方程；（注：系数b，a，d，c按四舍五入保留一位小数）
(2)根据下表中数据，用相关指数R2（不必计算，只比较大小）比较两种模型的拟合效果哪个更好，并选择拟合精度更高、更可靠的模型，预测当研发年投资额为8百万元时，产品的年销售量是多少？
参考公式及数据：b=i=1nxi−xyi−yi=1nxi−x2=i=1nxiyi−nxyi=1nxi2−nx2，a=y−bx，
R2=1−i=1nyi−yi2i=1nyi−y2=1−i=1nyi−yi2i=1nyi2−ny2，
i=16xizi=−1×0.7+2×0+3×0.4+4×1.1+5×1.8+6×2.5=28.9，e3.4=30.
【答案】(1)y=2.1x−3.4，y=e0.6x−1.4
(2)30（千件）
【分析】（1）求出x,y，根据公式计算出b,a得线性回归方程；求出z，再求得系数a，b，代入得非线性回归方程；
（2）根据（1）回归方程分别求得相关指数R12,R22，比较可得，然后估算销售量即可．
【详解】（1）由题可得x=161+2+3+4+5+6=3.5，y=160.5+1+1.5+3+6+12=4，
i=16xiyi=1×0.5+2×1+3×1.5+4×3+5×6+6×12=121，i=16xi2=1+4+9+16+25+36=91 ，
所以b=i=16xiyi−6xyi=16xi2−6x2=121−5×4×3.591−6×3.52≈2.11， a=y−bx=4−2.11×3.5≈−3.4，
方案①回归方程y=2.1x−3.4，
对y=edx+c两边取对数得：lny=dx+c，令z=lny，z=dx+c是一元线性回归方程.
z=16−0.7+0+0.4+1.1+1.8+2.5=0.85 ，
d=i=16xiyi−6xyi=16xi2−6x2=28.9−6×3.5×0.8591−6×3.52≈0.63，
c=z−dx=0.85−0.63×3.5≈−1.4，
方案②回归方程y=e0.6x−1.4 ；
（2）方案①相关指数R12=1−18.29i=1nyi2−ny2；
方案②相关指数R22=1−0.65i=1nyi2−ny2，
R12故模型②的拟合效果更好，精度更高.
当研发年投资额为8百万元时，产品的年销售量y=e4.8−1.4=e3.4=30（千件）.
7．（2023·全国·模拟预测）信创产业即信息技术应用创新产业，是一条规模庞大、体系完整的产业链，是数字经济的重要抓手之一．在政府、企业等多方面的共同努力下，中国信创产业市场规模不断扩大，市场释放出前所未有的活力．下表为2018—2022年中国信创产业规模（单位：千亿元），其中2018—2022年对应的代码依次为1~5．
(1)从2018—2022年中国信创产业规模中任取2个数据，求这2个数据都大于10的概率．
(2)由上表数据可知，可用指数型函数模型y=a⋅bx拟合y与x的关系，请建立y关于x的回归方程（a，b的值精确到0.01），并预测2023年中国信创产业规模能否超过20千亿元．
参考数据：
其中vi=lnyi，v=15i=15vi．
参考公式：对于一组数据u1,w1，u2,w2，…，un,wn，其回归直线w=α+βu的斜率和截距的最小二乘估计公式分别为β=i=1nuiwi−nuwi=1nui2−nu2，α=w+βu．
【答案】(1)310
(2)y=6.81×1.19x，不会超过20千亿元．
【分析】（1）根据古典概型概率计算公式，利用列举法可得2个数据都大于10的概率为310；（2）将指数型函数模型y=a⋅bx两边取对数可得lny=lna+xlnb，即v=lna+xlnb，再利用参考数据可得回归方程为y=6.81×1.19x，将2023年的年份代码6代入可得y≈19.34<20，即可得出结论.
【详解】（1）从2018—2022年中国信创产业规模中任取2个数据有
8.1,9.6，8.1,11.5，8.1,13.8，8.1,16.7，9.6,11.5，9.6,13.8，
9.6,16.7，11.5,13.8，11.5,16.7，13.8,16.7，共10种情况．
其中这2个数据都大于10的有11.5,13.8，11.5,16.7，13.8,16.7，共3种情况，
所以2个数据都大于10的概率P=310．
（2）y=a⋅bx两边同时取自然对数，
得lny=lna⋅bx=lna+xlnb，则v=lna+xlnb．
因为x=3，v=2.45，i=15xi2=55，
所以lnb=i=15xivi−5xvi=15xi2−5x2=38.52−5×3×2.4555−5×32=0.177，
lna=v−x⋅lnb=2.45−0.177×3=1.919，所以v=1.919+0.177x，
即lny=1.919+0.177x，所以y=e1.919+0.177x=6.81×1.19x，
即y关于x的回归方程为y=6.81×1.19x．
2023年的年份代码为6，把x=6代入y=6.81×1.19x，
得y=6.81×1.196=6.81×2.84≈19.34<20，
所以预测2023年中国信创产业规模不会超过20千亿元．
【考点3：非线性回归类型三：对数函数型】
【知识点：类型三：对数函数型】
1．（2023春·四川成都·高二统考期中）某校一个课外学习小组为研究某作物种子的发芽率y和温度x（单位：°C）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据xi,yii=1,2,⋯,20得到下面的散点图：
由此散点图，在10∘C至40∘C之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是（ ）
A．y=a+bxB．y=a+bx2
C．y=a+bexD．y=a+blnx
【答案】D
【分析】根据散点的分布可得出合适的回归方程类型.
【详解】由散点图可见，数据分布成递增趋势，但是呈现上凸效果，即增加缓慢.
A中，y=a+bx是直线型，均匀增长，不符合要求；
B中，y=a+bx2是二次函数型，函数y=a+bx2 b≠0对称轴为y轴，
当b>0时，图象呈现下凸，增长也较快，不符合要求；
当b<0时，图象呈现上凸，呈递减趋势，不符合要求；
C中，y=a+bex是指数型，爆炸式增长，增长快，不符合要求；
D中，y=a+blnx是对数型，增长缓慢，符合要求.
故对数型最适宜该回归模型.
故选：D.
2．（2023春·高二单元测试）发展扶贫产业，找准路子是关键，重庆市石柱土家族自治县中益乡华溪村不仅找准了路，还将当地打造成了种植中药材黄精的产业示范基地．通过种植黄精，华溪村村民的收入逐年递增．以下是2014年至2020年华溪村村民每户平均可支配收入的统计数据：
根据以上数据，绘制如图所示的散点图：
(1)根据散点图判断，y=a+bx与y=c+dlnx哪一个更适宜作为每户平均可支配收入y（千元）关于年份代码x的回归方程模型（给出判断即可，不必说明理由），并建立y关于x的回归方程（结果保留1位小数）；
(2)根据（1）建立的回归方程，试预测要到哪一年华溪村的每户平均可支配收入才能超过35（千元）；
参考数据：
其中ui=lnxi，u=17i=17ui．
参考公式：线性回归方程y=bx+a中，b=i=1nxi−xyi−yi=1nxi−x2，a=y−bx．
【答案】(1)y=c+dlnx更适宜作为每户平均可支配收入y（千元）关于年份代码x的回归方程模型，y=5.7+14.2lnx；
(2)到2022年每户平均可支配收入才能超过35（千元）；
【分析】（1）根据图象，随着年份增加，每户平均可支配收入增加趋于缓慢，对数模型更适合.
（2）根据回归直线的计算方法，可得y关于x的回归方程为y=5.7+14.2lnx.令y>35，最小的整数x即为所求年份代码.
【详解】（1）根据题中散点图，得y=c+dlnx更适宜作为每户平均
可支配收入y（千元）关于年份代码x的回归方程模型．
由已知数据，得
d=i=1nui−uyi−yi=1nui−u2 =i=17uiyi−7uyi=17ui2−7u2
=235.1−7×1.2×22.713.2−7×1.2×1.2≈14.2，
故c=y−du=22.7−14.2×1.2≈5.7，故y关于x的回归方程为y=5.7+14.2lnx.
（2）由题知，令5.7+14.2lnx>35，整理，得lnx>2.1，即x>e2.1≈8.2．
故当x=9时，即到2022年每户平均可支配收入才能超过35（千元）．
3．（2023春·吉林长春·高二长春十一高校考阶段练习）《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》，这是21世纪以来第18个指导“三农”工作的中央一号文件.文件指出，民族要复兴，乡村必振兴，要大力推进数字乡村建设，推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售，众多网红主播参与到直播当中，在众多网红直播中，统计了10名网红直播的观看人次xi和农产品销售量yii=1,2,3,⋯,10的数据，得到如图所示的散点图.
(1)利用散点图判断，y=a+bx和y=c+dlnx哪一个更适合作为观看人次x和销售量y的回归方程类型；（只要给出判断即可，不必说明理由）
(2)对数据作出如下处理：得到相关统计量的值如表：
其中令ωi=lnxi，ω=110i=110ωi.
根据（1）的判断结果及表中数据，求y（单位：千件）关于x（单位：十万次）的回归方程，并预测当观看人次为280万人时的销售量；
参考数据和公式：ln2≈0.69，ln7≈1.95
附：对于一组数据u1,v1、u2,v2、⋯、un,vn，其回归线v=α+βu的斜率和截距的最小二乘估计分别为：β=i=1nui−uvi−vi=1nui−u2，α=v−βu.
【答案】(1)y=c+dlnx更适合；
(2)y=10.3+10lnx，预测当观看人次为280万人时的销售量约为43600件.
【分析】（1）根据散点图中散点的分布情况可选择合适的回归模型；
（2）令ω=lnx，则y=c+dω，将表格中的数据代入最小二乘法公式，可求得d、c的值，进而可得出y关于x的回归方程，将x=28代入回归方程可得出销售量.
【详解】（1）解：由散点图可知，散点分布在一条对数型曲线附近，所以选择回归方程y=c+dlnx更适合.
（2）解：令ω=lnx，则y=c+dω，
因为i=110ωi−ωyi−y=66，i=110ωi−ω2=6.6，
所以d=i=110ωi−ωyi−yi=110ωi−ω2=666.6=10，
又因为y=30.3，ω=2，所以c=y−dω=30.3−10×2=10.3，
所以y与ω的线性回归方程为y=10.3+10ω，
故y关于x的回归方程为y=10.3+10lnx.
令x=28，代入回归方程可得y=10.3+10ln28=10.3+10×2ln2+ln7≈43.6（千件）
所以预测观看人次为280万人时的销售量约为43600件.
4．（2023·云南昆明·高三昆明一中校考阶段练习）《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》，这是21世纪以来第18个指导“三农”工作的中央一号文件.文件指出，民族要复兴，乡村必振兴，要大力推进数字乡村建设，推进智慧农业发展.某乡村合作社借助互联网直播平台进行农产品销售，众多网红主播参与到直播当中，在众多网红直播中，统计了10名网红直播的观看人次xi和农产品销售量yii=1,2,3,⋯,10的数据，得到如图所示的散点图.
(1)利用散点图判断，y=a+bx和y=c+dlnx哪一个更适合作为观看人次x和销售量y的回归方程类型；（只要给出判断即可，不必说明理由）
(2)对数据作出如下处理：得到相关统计量的值如表：
其中令ωi=lnxi，ω=110i=110ωi.根据（1）的判断结果及表中数据，求y关于x的回归方程，并预测当观看人次为280万人时的销售量；
(3)规定：观看人次大于等于120万人次的主播为优秀主播，从这10名主播中随机抽取3名，记其中优秀主播的人数为X，求X的分布列和数学期望.
参考数据和公式：ln2≈0.69，ln7≈1.95
附：对于一组数据u1,v1，u2,v2，…，un,vn，其回归线v=α+βu的斜率和截距的最小二乘估计分别为：β=i=1nui−uvi−vi=1nui−u2，α=v−βu.
【答案】(1)y=c+dlnx更适合
(2)y=10.3+10lnx，43600件
(3)分布列见解析，65
【分析】（1）观察散点图，根据散点的分布规律判断应采用的模型；
（2）令ω=lnx，先求y与ω的线性回归方程，由此可得y与x的回归方程，再利用回归方程预测；
（3）确定随机变量的X的可能取值，再求取各值的概率，由此可得X的分布列，利用均值公式求其期望.
【详解】（1）由散点图可知，散点分布在一条对数型曲线附近，
所以选择回归方程y=c+dlnx更适合；
（2）令ω=lnx，则y=c+dω，
因为i=110ωi−ωyi−y=66，i=110ωi−ω2=6.6，
所以d=i=110ωi−ωyi−yi=110ωi−ω2=666.6=10，
又y=30.3，ω=2，
所以c=y−dω=30.3−10×2=10.3，
所以y与ω的线性回归方程为y=10.3+10ω，
故y关于x的回归方程为y=10.3+10lnx.
令x=28，代入回归方程可得y=10.3+10ln28=10.3+10×2ln2+ln7≈43.6（千件），
所以预测观看人次为280万人时的销售量约为43600件.
（3）由散点图可知，这10名主播中，优秀主播的个数有4个，
所以X的可能取值为0，1，2，3，
所以PX=0=C63C40C103=16，PX=1=C62C41C103=12，
PX=2=C61C42C103=310，PX=3=C60C43C103=130，
所以X的分布列为：
数学期望EX=0×16+1×12+2×310+3×130=65.
5．（2023·山西·校联考模拟预测）某剧场的座位数量是固定的，管理人员统计了最近在该剧场举办的五场表演的票价xi（单位：元）和上座率yi（上座人数与总座位数的比值）的数据，其中i=1，2，3，4，5，并根据统计数据得到如下的散点图：
(1)由散点图判断y=bx+a与y=clnx+d哪个模型能更好地对y与x的关系进行拟合（给出判断即可，不必说明理由），并根据你的判断结果求回归方程；
(2)根据（1）所求的回归方程，预测票价为多少时，剧场的门票收入最多．
参考数据：x=240,y=0.5，i=15xi2=365000，i=15xiyi=457.5；设zi=lnxi，则i=15zi≈27，i=15zi2≈147.4，i=15ziyi≈12.7；e5.2≈180，e5.4≈220，e6.4≈600．
参考公式：对于一组数据u1,v1,u2,v2,⋯,un,vn，其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：β=i=1nuivi−nuvi=1nui2−nu2=i=1nui−uvi−vi=1nui−u2，α=v−βu．
【答案】(1)y=clnx+d能更好地对y与x的关系进行拟合，y=−0.5lnx+3.2；
(2)预测票价为220元时，剧场的门票收入最多．
【分析】（1）由散点图知，y=clnx+d能更好地对y与x的关系进行拟合，设z=lnx，由公式求出c，再将y,z代入求出d，可得y关于z的线性回归方程，进而得出y关于x的回归方程；
（2）设函数fx=−0.5xlnx+3.2x，对函数求导，判断出单调性和极值，可预测剧场的门票收入最多时的票价．
【详解】（1）y=clnx+d能更好地对y与x的关系进行拟合．
设z=lnx，先求y关于z的线性回归方程．
由已知得z=15i=15zi≈275=5.4，
所以c=i=15ziyi−5zyi=15zi2−5z2≈12.7−5×5.4×0.5147.4−5×5.42=12.7−13.5147.4−145.8=−−0.5，
d=y−cz=0.5−−0.5×5.4=3.2，
所以y关于z的线性回归方程为y=−0.5z+3.2，
所以y关于x的回归方程为y=−0.5lnx+3.2；
（2）设该剧场的总座位数为M，由题意得门票收入为M−0.5xlnx+3.2x，
设函数fx=−0.5xlnx+3.2x，则f′(x)=−0.5lnx+2.7，
当f′(x)<0，即x>e5.4时，函数单调递减，当f′(x)>0，即0所以f(x)在x=e5.4≈220处取最大值，
所以预测票价为220元时，剧场的门票收入最多．
6．（2023·辽宁朝阳·校联考一模）秋天的第一杯奶茶是一个网络词汇，最早出自四川达州一位当地民警之口，民警用“秋天的第一杯奶茶”顺利救下一名女孩，由此而火爆全网.后来很多人开始在秋天里买一杯奶茶送给自己在意的人.某奶茶店主记录了入秋后前7天每天售出的奶茶数量（单位：杯）
如下：
(1)请根据以上数据，绘制散点图，并根据散点图判断，y=a+bx与y=c+dlnx哪一个更适宜作为y关于x的回归方程模型（给出判断即可，不必说明理由）；
(2)建立y关于x的回归方程（结果保留1位小数），并根据建立的回归方程，试预测要到哪一天售出的奶茶才能超过35杯？
(3)若每天售出至少25杯即可盈利，则从第一天至第七天中任选三天，记随机变量X表示盈利的天数，求随机变量X的分布列.
参考公式和数据：其中ui=lnxi,u=17i=17ui
回归直线方程y=bx+a中，b=i=1nx1y1−nxyi=1nxi2−nx2,a=y−bx
【答案】(1)图见解析，y=c+dlnx更适宜作为y关于x的回归方程模型；
(2)yˆ=5.7+14.2lnx，到第9天才能超过35杯；
(3)分布列见解析.
【分析】(1)根据散点图趋势即可判断；
(2)利用非线性回归方程转化为线性回归方程的方法求解；
(3)根据超几何分布求分布列.
【详解】（1）
根据散点图，知y=c+dlnx更适宜作为y关于x的回归方程模型；
（2）令u=lnx，则y=c+du，
由已知数据得d=i=17x1y1−nxyi=17xi2−nx2=235.1−7×22.7×1.213.2−7×1.2×1.2≈14.2，
c=y−du=22.7−14.2×1.2≈5.7，
所以y=5.7+14.2u，
故y关于x的回归方程为yˆ=5.7+14.2lnx，
进而由题意知，令5.7+14.2lnx>35，整理得lnx>2.1，即x>e2.1≈8.2，
故当x=9时，即到第9天才能超过35杯；
（3）由题意知，这7天中销售超过25杯的有4天，则随机变量X的可能取值为0,1,2,3
PX=0=C40C33C73=135，PX=1=C41C32C73=1235，
PX=2=C42C31C73=1835，PX=3=C43C30C73=435，
则随机变量X的分布列为
7．（2023·全国·高三专题练习）一所中学组织学生对某线下某实体店2022年部分月份的月利润情况进行调查统计，得到的数据如下：
根据散点图，准备用①y=alnx+b或②y=cx+d建立y关于x的回归方程.
(1)用线性相关系数说明上面的两种模型哪种适宜作为y关于x的回归方程?
(2)由参考数据，根据（1）的判断结果，求y关于x的回归方程（精确到0.1）.
附：对于一组数据ui,vi（i=1，2，3，⋯，n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=i=1nui−uvi−vi=1nui−u2，α=v−βu.相关系数r=i=1nui−uvi−vi=1nui−u2i=1nvi−v2.
参考数据：x=7，y=3.55，λ=1.80，μ=2.55，i=16λi−λ2=2.20，
i=16μi−μ2=2.89，i=16yi−yλi−λ=5.55，i=16yi−yμi−μ=6.32，
i=16yi−y2i=16λi−λ2=5.76，i=16yi−y2i=16μi−μ2=6.61.
【答案】(1)模型①
(2)y=2.5lnx−1.0
【分析】(1)计算相关系数比较大小即可确定更适宜的模型；
(2)利用最小二乘法相关公式即可求解.
【详解】（1）由题意y=aλ+b的线性相关系数的相关系数
r1=i=16yi−yλi−λi=16yi−y2i=16λi−λ2=≈0.963.
y=cx+d的相关系数r2=i=16yi−yμi−μi=16yi−y2i=16μi−μ2=≈0.956.
所以1>r1>r2>0，因此模型①拟合效果更好.
（2）根据（1）的判断结果，
计算a与b由参考数据a=i=16yi−yλi−λi=16λi−λ2=≈2.52，∴a=2.5
所以b=y−2.52×λ≈−1.0.
于是y关于x的回归方程①为y=2.5lnx−1.0.
8．（2023·福建·统考模拟预测）放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节，运行效率不断提升.以下是根据近10年年份数xi与该机场飞往A地航班放行准点率yi（i=1，2，⋯，10）（单位：百分比）的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
其中ti=lnxi−2012，t=110i=110ti
(1)根据散点图判断，y=bx+a与y=clnx−2012+d哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型（给出判断即可，不必说明理由），并根据表中数据建立经验回归方程，由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地､B地和其他地区的航班比例分别为0.2、0.2和0.6.若以（1）中的预测值作为2023年该机场飞往A地航班放行准点率的估计值，且2023年该机场飞往B地及其他地区（不包含A、B两地）航班放行准点率的估计值分别为80%和75%，试解决以下问题：
（i）现从2023年在该机场起飞的航班中随机抽取一个，求该航班准点放行的概率；
（ii）若2023年某航班在该机场准点放行，判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大，说明你的理由.
附：（1）对于一组数据u1,v1，u2,v2，…，un,vn，其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=i=1nui−uvi−vi=1nui−u2=i=1nuivi−nu⋅vi=1nui2−nu2，α=v−βu
参考数据：ln10≈2.30，ln11≈2.40，ln12≈2.48.
【答案】(1)y=clnx−2012+d适宜，预测2023年该机场飞往A地的航班放行准点率84%
(2)（i）0.778；（ii）可判断该航班飞往其他地区的可能性最大，理由见解析
【分析】（1）根据线性回归方程的计算公式，选择合适的模型计算即可；
（2）利用全概率公式和条件概率公式，即可根据概率判断可能性最大的情况.
【详解】（1）由散点图判断y=clnx−2012+d适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型.
令t=lnx−2012，先建立y关于t的线性回归方程.
由于c=i=110tiyi−10tyi=1−10ti2−10t−2=1226.8−10×1.5×80.427.7−10×1.52=4，
d=y−ct=80.4−4×1.5=74.4，
该机场飞往A地航班放行准点率y关于t的线性回归方程为y=4t+74.4，
因此y关于年份数x的回归方程为y=4lnx−2012+74.4
所以当x=2023时，该机场飞往A地航班放行准点率y的预报值为
y=4ln2023−2012+74.4=4ln11+74.4≈4×2.40+74.4=84.
所以2023年该机场飞往A地航班放行准点率y的预报值为84%.
（2）设A1=“该航班飞往A地”，A2=“该航班飞往B地”，A3=“该航班飞往其他地区”，C=“该航班准点放行”，
则PA1=0.2，PA2=0.2，PA3=0.6，
PCA1=0.84，PCA2=0.8，PCA3=0.75.
（i）由全概率公式得，
PC=PA1PCA1+PA2PCA2+PA3PCA2
=0.84×0.2+0.8×0.2+0.75×0.6=0.778，
所以该航班准点放行的概率为0.778.
（ii）PA1C=PA1CPC=PA1PCA1PC=0.2×，
PA2C=PA2CPC=PA2PCA2PC=0.2×，
PA3C=PA3CPC=PA3PCA3PC=0.6×，
因为0.6×0.75>0.2×0.84>0.2×0.8，
所以可判断该航班飞往其他地区的可能性最大.
曲线方程
变换公式
变换后的线性关系式
周数x
1
2
3
4
5
治愈人数y
2
17
36
93
142
y
i=15xi2
i=15xi4
i=15xiyi
i=15xi2yi
34
55
979
657
2805
年份
2016
2017
2018
2019
2020
2021
2022
广告费支出x
1
2
4
6
11
13
19
销售量y
1.9
3.2
4.0
4.4
5.2
5.3
5.4
i=15ui
i=15vi
i=15ui−uvi−v
i=15ui−u2
16.10
26.02
0.40
1.60
x
y
t
i=120xi−x2
i=120ti−t2
i=120yi−yxi−x
i=120yi−yti−t
14.5
10
0.08
665
0.04
-450
4
t
1
2
3
4
5
y
507
144
72
32
25
年份
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
每周人均读书时间y（小时）
1.3
2.8
5.7
8.9
13.8
年份
2018年
2019年
2020年
2021年
2022年
年份代码x
1
2
3
4
5
云计算市场规模y/千万元
7.4
11
20
36.6
66.7
z=lny
2
2.4
3
3.6
4
天数x
1
2
3
4
5
6
繁殖个数y
6
12
25
49
95
190
x
y
z
i=16xi−x2
i=16xi−xy1−y
i=16xi−xzi−z
3.50
62.83
3.53
17.50
596.57
12.09
x
1
2
3
4
5
y
0.5
1
1.5
3
5.5
表1
x
1
2
3
4
5
z=lny
−0.7
0
0.4
1.1
1.7
表2
x
1
2
3
4
5
y
0.5
1
1.5
3
5.5
y
0.54
0.96
1.74
3.15
5.67
x
1
2
3
4
5
6
y
0.5
1
1.5
3
6
12
z=lny
-0.7
0
0.4
1.1
1.8
2.5
经验回归方程残差平方和
y=bx+a
y=edx+c
i=15yi−yi2
18.29
0.65
年份代码x
1
2
3
4
5
中国信创产业规模y/千亿元
8.1
9.6
11.5
13.8
16.7
v
i=15xivi
e1.919
e0.177
1.196
2.45
38.52
6.81
1.19
2.84
年份
2014
2015
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
6
7
每户平均可支配收入y（千元）
4
15
22
26
29
31
32
y
u
i=17xiyi
i=17uiyi
i=17ui2
e2.1
22.7
1.2
759
235.1
13.2
8.2
x
y
ω
i=110xi−x2
i=110ωi−ω2
i=110xi−xyi−y
i=110ωi−ωyi−y
9.4
30.3
2
366
6.6
439.2
66
x
y
ω
i=110xi−x2
i=110ωi−ω2
i=110xi−xyi−y
i=110ωi−ωyi−y
9.4
30.3
2
366
6.6
439.2
66
X
0
1
2
3
P
16
12
310
130
日期
第一天
第二天
第三天
第四天
第五天
第六天
第七天
日期代码x
1
2
3
4
5
6
7
杯数y
4
15
22
26
29
31
32
y
u
i=17xiy1
i=17uiy1
i=17ui2
e2.1
22.7
1.2
759
235.1
13.2
8.2
X
0
1
2
3
P
135
1235
1835
435
月份x
2
4
6
8
10
12
净利润y（万元）
0.9
2.0
4.2
3.9
5.2
5.1
λ=lnx
0.7
1.4
1.8
2.1
2.3
2.5
μ=x
1.4
2.0
2.4
2.8
3.2
3.5
x
y
t
i=110xi2
i=110xiyi
i=110ti2
i=110tiyi
2017.5
80.4
1.5
40703145.0
1621254.2
27.7
1226.8