2022-2023学年天津市河西区七年级上册期末数学试卷及答案

这是一份2022-2023学年天津市河西区七年级上册期末数学试卷及答案，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 计算：的结果等于（）
A. B. C. 7D. 3
【答案】A
2. 下列各组数中，互为相反数的是（ ）
A. 2与B. 与1C. 与D. 2与
【答案】C
3. 天津到上海的铁路里程约米，用科学记数法表示的结果（）
A. B. C. D.
【答案】B
4. 由5个小立方体搭成如图所示的几何体，从左面看到的平面图形是（）
A. B. C. D.
【答案】D
5. 下列方程变形正确的是（）
A. 由得B. 由得
C. 由得D. 由得
【答案】C
6. 下列说法正确的是（ ）
A. 一点确定一条直线
B. 两条射线组成的图形叫角
C. 两点之间线段最短
D. 若AB=BC，则B为AC的中点
【答案】C
7. 下列各组中的两个单项式为同类项的是（）
A. 和B. 和
C和D. 和
【答案】D
8. 在灯塔O处观测到轮船A位于南偏东的方向，同时轮船B位于北偏东的方向，那么的大小为（）
A. B. C. D.
【答案】A
9. 父亲与小强下棋（设没有平局），父亲胜一盘记2分，小强胜一盘记3分，下了10盘后，两人得分相等，则小强胜的盘数是（ ）
A. 2B. 3C. 4D. 5
【答案】C
10. 如图，长为的长方形，沿图中虚线裁剪成四个形状大小完全相同的小长方形，那么每个小长方形的周长为（）（用含a的式子表示）
A. B. C. D.
【答案】C
二、填空题：（本大题共6小题，每小题3分，共18分.）
11. 单项式的次数是____________．
【答案】
12. 计算的结果等于______.
【答案】
13. 已知方程（a﹣5）x|a|﹣4+2=0是关于x的一元一次方程，则a的值是_____．
【答案】-5
14. ____________．
【答案】
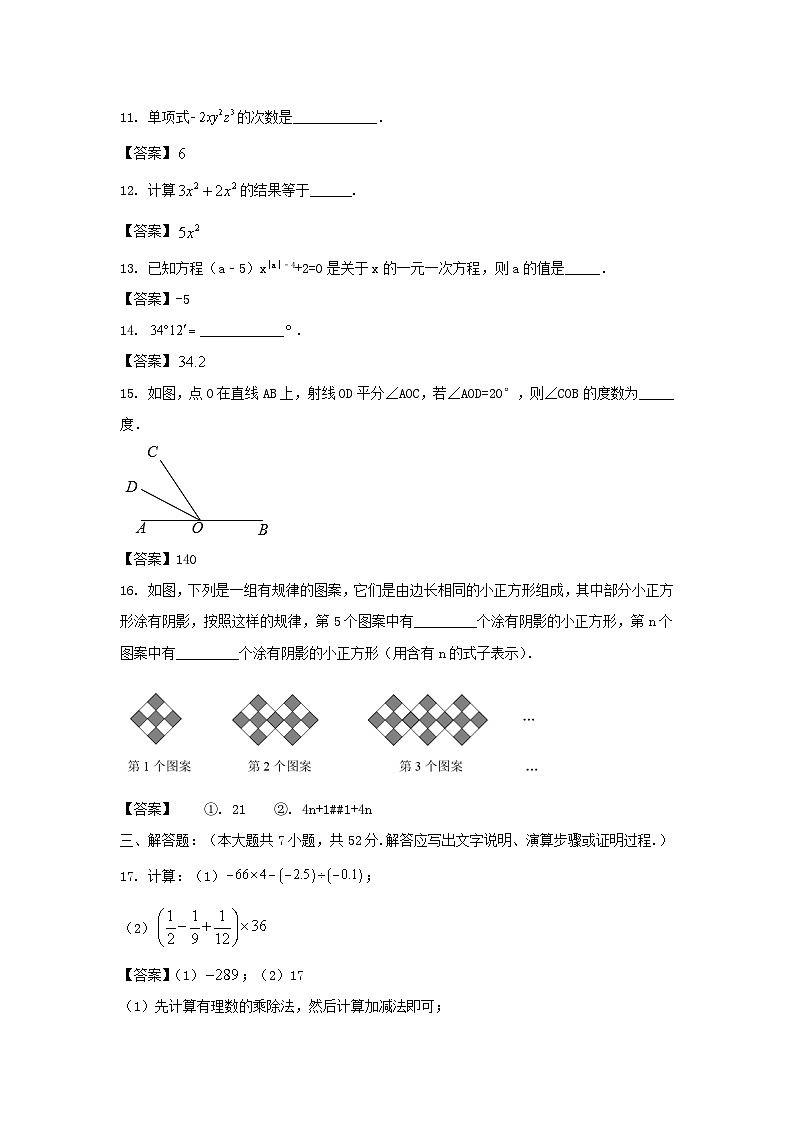
15. 如图，点O在直线AB上，射线OD平分∠AOC，若∠AOD=20°，则∠COB的度数为_____度．
【答案】140
16. 如图，下列是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，按照这样的规律，第5个图案中有_________个涂有阴影的小正方形，第n个图案中有_________个涂有阴影的小正方形（用含有n的式子表示）．
【答案】 ①. 21 ②. 4n+1##1+4n
三、解答题：（本大题共7小题，共52分.解答应写出文字说明、演算步骤或证明过程.）
17. 计算：（1）；
（2）
【答案】（1）；（2）17
（1）先计算有理数的乘除法，然后计算加减法即可；
（2）利用乘法分配律计算即可．
【详解】解：（1）
；
（2）
．
18. 解下列方程：
（1）（2）
【答案】（1）；（2）.
（1）先去括号，然后移项、合并，系数化为1，即可得到答案；
（2）先去分母、去括号，然后移项、合并，系数化为1，即可得到答案.
【详解】解：（1），
∴，
∴，
∴；
（2），
∴，
∴，
∴，
∴.
19. 已知，
（1）求；
（2）若，求的值
【答案】（1）；（2）57
（1）根据整式的混合运算，即可得到答案；
（2）利用绝对值的非负性求出x、y的值，然后代入计算，即可得到代数式的值.
【详解】解：（1）∵，，
∴
=
=；
（2）∵，
∴，，
∴，，
∴原式=
=
=.
20. 如图，已知B、C两点把线段分成三部分，M为的中点，，求的长．
【答案】的长为20
由题意得AB=AD，由中点的定义可知AM=AD，从而可得到AD−AD=6，从而可求得AD的长．
详解】解：∵B、C两点把线段AD分成2：5：3三部分，
∴AB=AD，CD=AD．
∵M为AD的中点，
∴AM=AD．
∵BM=AM-AB，
∴AD−AD=6．
解得：AD=20．
答：的长为20．
21. 如图，已知∠BOC=2∠AOB，OD平分∠AOC，∠BOD=14°，求∠AOC的度数．
【答案】∠AOC=84°．
此题可以设∠AOB=xº，∠BOC=2xº，再进一步表示∠AOC=3xº，根据角平分线的概念表示∠AOD，最后根据∠AOD-∠AOB=∠BOD，列方程即可计算．
【详解】解：设∠AOB=xº，∠BOC=2xº.
则∠AOC=3xº，
又OD平分∠AOC，
∴∠AOD=x，
∴∠BOD=∠AOD−∠AOB=x−x=14º，
∴x=28º，
即∠AOC=3x=3×28º=84º.
22. 国庆节期间，甲、乙两商场以相同价格出售同样的商品，并且各自推出不同的优惠方案：在甲商场累计购物超过元后，超出的部分打八五折收费；在乙商场累计购物超过元后，超出的部分打九折收费．设小华预计累计购物x元（）．
（1）计算一下，小华预计累计购物多少元商品时，到两个商场购物实际所付的费用相同？
（2）如果小华预计累计购物元商品，她选哪个商场购物比较合适？说明理由．
【答案】（1）500元
（2）甲商场，理由见解析
（1）根据题意表示出两个商场的费用，列方程即可；
（2）分别求出在两个商场的费用比较大小即可．
【小问1详解】
解：设小华累计购物x元（），到两个商场购物实际所付的费用相同．
根据题意，得．
整理，得，
解得．
答：小华累计购物500元商品时，到两个商场购物实际所付的费用相同．
【小问2详解】
解：当累计购物600元商品时，
在甲商场购物所付的费用为（元），
在乙商场购物所付的费用为（元）．
因为，
所以小华选甲商场购物比较合适．
23. 已知线段AB＝m（m为常数），点C为直线AB上一点，点P、Q分别在线段BC、AC上，且满足CQ＝2AQ，CP＝2BP．
（1）如图，若AB＝6，当点C恰好在线段AB中点时，则PQ＝ ；
（2）若点C为直线AB上任一点，则PQ长度是否为常数？若是，请求出这个常数；若不是，请说明理由；
（3）若点C在点A左侧，同时点P在线段AB上（不与端点重合），请判断2AP+CQ﹣2PQ与1的大小关系，并说明理由．
【答案】（1）4；（2）PQ是一个常数，即是常数m；（3）2AP+CQ﹣2PQ＜1，见解析．
（1）根据已知AB＝6，CQ＝2AQ，CP＝2BP，以及线段的中点的定义解答；
（2）由题意根据已知条件AB＝m（m为常数），CQ＝2AQ，CP＝2BP进行分析即可；
（3）根据题意，画出图形，求得2AP+CQ﹣2PQ＝0，即可得出2AP+CQ﹣2PQ与1的大小关系．
详解】解：（1）∵CQ＝2AQ，CP＝2BP，
∴CQ＝AC，CP＝BC，
∵点C恰好在线段AB中点，
∴AC＝BC＝AB，
∵AB＝6，
∴PQ＝CQ+CP＝AC+BC＝×AB+×AB＝×AB＝×6＝4；
故答案为：4；
（2）①点C在线段AB上：
∵CQ＝2AQ，CP＝2BP，
∴CQ＝AC，CP＝BC，
∵AB＝m（m为常数），
∴PQ＝CQ+CP=AC+BC＝×（AC+BC）＝AB=m；
②点C在线段BA的延长线上：
∵CQ＝2AQ，CP＝2BP，
∴CQ＝AC，CP＝BC，
∵AB＝m（m为常数），
∴PQ＝CP﹣CQ＝BC﹣AC＝×（BC﹣AC）＝AB＝m；
③点C在线段AB的延长线上：
∵CQ＝2AQ，CP＝2BP，
∴CQ＝AC，CP＝BC，
∵AB＝m（m为常数），
∴PQ＝CQ﹣CP＝AC﹣BC＝×（AC﹣BC）＝AB＝m；
故PQ是一个常数，即是常数m；
（3）如图：
∵CQ＝2AQ，
∴2AP+CQ﹣2PQ
＝2AP+CQ﹣2（AP+AQ）
＝2AP+CQ﹣2AP﹣2AQ
＝CQ﹣2AQ
＝2AQ﹣2AQ
＝0，
∴2AP+CQ﹣2PQ＜1．