北京市东城区2023-2024学年九年级上学期期末数学试题

这是一份北京市东城区2023-2024学年九年级上学期期末数学试题，共12页。试卷主要包含了考试结束后，请将答题卡交回等内容，欢迎下载使用。

2024.1
学校班级姓名教育ID号
考生须知：
1.本试卷共8页，共三道大题，28道小题，满分100分，考试时间120分钟.
2.在试卷和答题卡上准确填写学校、班级、姓名和教育ID号.
3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效.
4.在答题卡上选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答.
5.考试结束后，请将答题卡交回.
一、选择题（每题2分，共16分）
1.下列四个交通标志图案中，是中心对称图形的是（ ）
A.B.C.D.
2.若是关于x的方程的一个根，则m的值是（ ）
A.B.C.3D.15
3.关于二次函数，下列说法正确的是（ ）
A.当时，有最小值为2B.当时，有最大值为2
C.当时，有最小值为2D.当时，有最大值为2
4.在下列事件中，随机事件是（ ）
A.投掷一枚质地均匀的骰子，向上一面的点数不超过6
B.从装满红球的袋子中随机摸出一个球，是白球
C.通常情况下，自来水在结冰
D.投掷一枚质地均匀的骰子，向上一面的点数为2
5.如图，正方形的边长为6，且顶点A，B，C，D都在上，则的半径为（ ）
A.3B.6C.D.
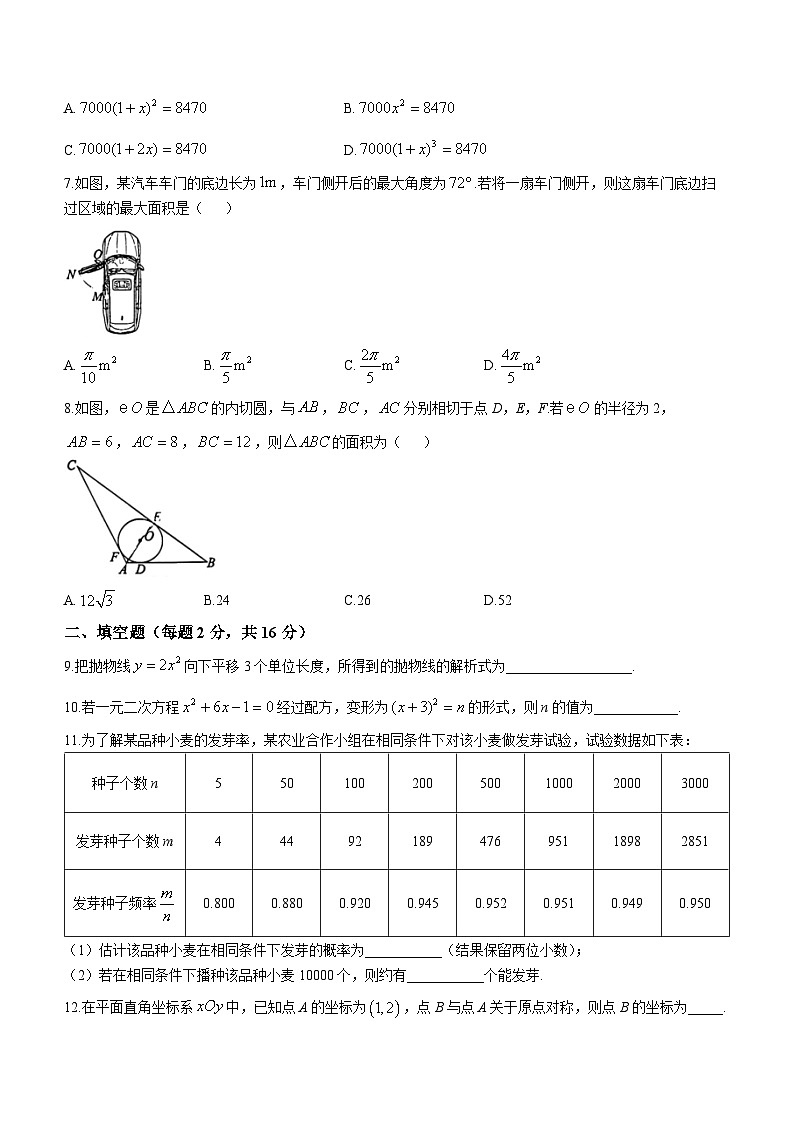
6.北京2022年冬奥会以后，冰雪运动的热度持续.某地滑雪场第一周接待游客7000人，第三周接待游客8470人.设该地滑雪场游客人数的周平均增长率为x，根据题意，下面所列方程正确的是（ ）
A.B.
C.D.
7.如图，某汽车车门的底边长为，车门侧开后的最大角度为.若将一扇车门侧开，则这扇车门底边扫过区域的最大面积是（ ）
A.B.C.D.
8.如图，是的内切圆，与，，分别相切于点D，E，F.若的半径为2，，，，则的面积为（ ）
A.B.24C.26D.52
二、填空题（每题2分，共16分）
9.把抛物线向下平移3个单位长度，所得到的抛物线的解析式为__________________.
10.若一元二次方程经过配方，变形为的形式，则n的值为____________.
11.为了解某品种小麦的发芽率，某农业合作小组在相同条件下对该小麦做发芽试验，试验数据如下表：
（1）估计该品种小麦在相同条件下发芽的概率为___________（结果保留两位小数）；
（2）若在相同条件下播种该品种小麦10000个，则约有___________个能发芽.
12.在平面直角坐标系中，已知点A的坐标为，点B与点A关于原点对称，则点B的坐标为_____.
13.已知二次函数，当时，y随x的增大而减小，则m的值可以是___________（写出一个即可）.
14.如阁，A，B，C是上的三个点，若，则的大小是___________.
15.如图1，一名男生推铅球，铅球的运动路线近似是抛物线的一部分，铅球出手位置的高度为，当铅球行进的水平距离为时，高度达到最大值.铅球的行进高度y（单位：）与水平距离x（单位：）之间的关系满足二次函数.若以最高点为原点，过原点的水平直线为x轴，建立如图2所示的平面直角坐标系，该二次函数的解析式为.若以过出手点且与地面垂直的直线为y轴，y轴与地面的交点为原点，建立如图3所示的平面直角坐标系，则该二次函数的解析式为_______________________.
图1图2图3
16.某单位承担了一项施工任务，完成该任务共需A，B，C，D，E，F，G七道工序，施工要求如下：
①先完成工序A，B，C，再完成工序D，E，F，最后完成工序G；
②完成工序A后方可进行工序B，工序C可与工序A，B同时进行；
③完成工序D后方可进行工序E，工序F可与工序D，E同时进行；
④完成各道工序所需时间如下表所示：
（1）在不考虑其它因素的前提下，该施工任务最少__________天完成；
（2）现因情况有变，需将工期缩短到80天，工序A，C，D每缩短1天需增加的投入分别为5万元，4万元，6万元，其余工序所需时间不可缩短，则所增加的投入最少是___________万元.
三、解答题（共68分，17-21题，每题5分，22题6分，23题5分，24-26题，每题6分，27-28题，每题7分）
17.解方程：.
18.如图，在中，.
求作：，使得的三个顶点都在上.
作法：
①作边的垂直平分线，交于点O；
②以点O为圆心，长为半径作圆.
则为所求作的圆.
（1）利用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面的证明.
证明：连接.
由作图可知，，
点B在上，
在中，，
（）（填推理依据）.
.
点C在上.
的三个顶点都在上.
19.在平面直角坐标系中，二次函数的图象过点.
（1）求该二次函数的解析式；
（2）用描点法画出该二次函数的图象；
（3）当时，对于x的每一个值，都有，直接写出k的取值范围.
20.某班开展“讲数学家故事”的活动.下面是印有四位中国数学家纪念邮票图案的卡片A，B，C，D，卡片除图案外其它均相同.将四张卡片背面朝上，洗匀后放在桌面上，小明同学从中随机抽取两张，讲述卡片上数学家的故事.
（1）请写出小明抽到的两张卡片所有可能出现的结果；
（2）求小明抽到的两张卡片中恰好有数学家华罗庚邮票图案的概率.
21.如图，是的弦，半径于点C.若，，求的半径的长.
22.已知关于x的一元二次方程.
（1）当该方程有两个不相等的实数根时，求m的取值范围；
（2）当该方程的两个实数根互为相反数时，求m的值.
23.如图，在边长均为1个单位长度的小正方形组成的网格中，O，B为格点（每个小正方形的顶点叫做格点），，，且，线段关于直线对称的线段为，将线段绕点O逆时针旋转得到线段.
（1）画出线段、；
（2）将线段绕点O逆时针旋转得到线段，连接.若，求的度数.
24.如图，为的直径，点C在上，的平分线交于点D，过点D作，交的延长线于点E.
（1）求证：直线是的切线；
（2）若，.求的长.
25.食用果蔬前，适当浸泡可降低农药的残留.某小组针对同种果蔬研究了不同浸泡方式对某种农药去除率的影响.
方式一：采用清水浸泡.
记浸泡时间为t分钟，农药的去除率为，部分实验数据记录如下：
方式二：采用不同浓度的食用碱溶液浸泡相同时间.
记食用碱溶液的浓度为，农药的去除率为，部分实验数据记录如下：
结合实验数据和结果，解决下列问题：
（1）通过分析以上实验数据，发现可以用函数刻画方式一中农药的去除率与浸泡时间t（分）之间的关系，方式二中农药的去除率与食用碱溶液的浓度之间的关系，请分别在下面的平面直角坐标系中画出这两个函数的图象；
（2）利用方式一的函数关系可以推断，降低该种农药残留的最佳浸泡时间约为___________分钟；
（3）利用方式一和方式二的函数关系可以推断，用食用碱溶液浸泡含该种农药的这种果蔬时，要想不低于清水浸泡的最大去除率，食用碱溶液的浓度中，x的取值范围可以是______________.
26.在平面直角坐标系中，点在抛物线上，设该抛物线的对称轴为直线.
（1）求t的值；
（2）已知，是该抛物线上的任意两点，对于，，都有，求m的取值范围.
27.在中，，，D为上一点，连接，将线段绕点D顺时针旋转得到线段.
（1）如图1，当点D与点B重合时，连接，交于点H，求证：；
图1
（2）当时（图2中，图3中），F为线段的中点，连接.在图2，图3中任选一种情况，完成下列问题：
图2图3
①依题意，补全图形.
②猜想的大小，并证明.
28.在平面直角坐标系中，已知点P和直线，，点P关于直线，“和距离”的定义如下：若点P到直线，的距离分别为，，则称为点P关于直线，的“和距离”，记为d.特别地，当点P在直线上时，；当点P在直线上时，.
备用图
（1）在点，，，中，关于x轴和y轴的“和距离”为3的点是____________；
（2）若P是直线上的动点，则点P关于x铀和y轴的“和距离”d的最小值为____________；
（3）已知点，的半径为1.若P是上的动点，直接写出点P关于x轴和直线的“和距离”d的取值范围.种子个数n
5
50
100
200
500
1000
2000
3000
发芽种子个数m
4
44
92
189
476
951
1898
2851
发芽种子频率
0.800
0.880
0.920
0.945
0.952
0.951
0.949
0.950
工序
A
B
C
D
E
F
C
所需时间/天
11
15
28
17
16
31
25
t（分）
5
8
10
12
15
20
30
50
57
52
37
33
2
5
7
10
12
15
43
52
57
76
57
25
东城区2023-2024学年度第一学期期末统一检测
初三数学参考答案及评分标准
一、选择题（每题2分，共16分）
二、填空题（每题2分，共16分）
9. 10.10 11.（1）0.95（2）9500 12.
13.答案不唯一，即可 14.50 15. 16.（1）86（2）38
三、解答题（共68分，17-21题，每题5分，22题6分，23题5分，24-26题，每题6分，27-28题，每题 7分）
17.解：移项，得.
因式分解，得.
于是得，或.
所以方整的两个根分别为，.
18.解：（1）作图如下，
（2）AB 直角三角形斜边上的中线等于斜边的一半
19.解：（1）点在二次函数的图象上，
，解得.
设二次函数的解析式为.
（2）列表：
描点，连线：
（3）
20.解：（1）所有可能出现的结果共6种：AB，AC，AD，BC，BD，CD.
（2）记抽到的两张卡片中恰好有数学家华罗庚邮票图案为事件M，M包含的结果有3种，即AC，BC，CD，且6种可能的结果出现的可能性相等.
所以.
21.解：连接OA.
半径于点C，，，
设，则，
在中，根据勾股定理，得，
即，解得.
的半径的长为17.
22.略
23.解：（1）如图
（2）略
24.（1）证明，如图1，连接.
是的直径，，
平分，
，，
，，
，
为的半径，
直线是的切线.
图1
（2）如图2，过点作于点F，，
，，.
在中，，
根据勾股定理，得，
，
，
在中，根据勾股定理，得
.
图2
25.解：（1）画图如下，
（2）10
（3）答案不唯一，如
26.解：（1）由题意可知，，.
（2）略
27.（1）证明，，，
将线段绕点顺时针旋转得到线段，
，，是等边三角形.
，，
（2）解：选择图2：
①补全图形如图所示：
②猜想.
证明：如图，过点作于点，连接.
则，
，，
，，，
为线段中点，，.
由（1）可知是等边三角形，
，，，
在利中，
（SAS），，
选择图3：
①补全图形如图所示：
②
（选择图3的答案与选择图2的答案一致）
28.解：（1）和.
（2）3.
（3）.题号
1
2
3
4
5
6
7
8
答案
B
C
A
D
C
A
B
C
x
…
0
1
2
3
…
y
…
3
0
0
3
…