期末经典题型检测卷2023-2024学年苏科版数学九年级上册

这是一份期末经典题型检测卷2023-2024学年苏科版数学九年级上册，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．社会主义本质是解放生产力，发展生产力，消灭剥削，消除两极分化，最终达到共同富裕．下列有关居民收入的统计量中，最能体现发展生产力，消除两极分化的是（ ）
A．收入平均数变小，方差变大B．收入平均数变小，方差变小
C．收入平均数变大，方差变大D．收入平均数变大，方差变小
2．已知关于的一元二次方程有两个相等的实数根，则此方程的根是（ ）
A．B．C．D．
3．已知，，…，的平均数为2，则，，…，的平均数是（ ）
A．9B．4C．3D．2
4．在一个半径为的圆内，有一个圆心角为的扇形，这个扇形的面积为（ ）
A．B．C．D．
5．近几年，手机支付用户规模增长迅速，据统计2020年手机支付用户约为亿人，连续两年增长后，2022年手机支付用户达到约亿人，已知第二年的增长率是第一年的增长率的2倍，如果设手机支付用户的第一年的增长率为则根据题意可以列出方程为（ ）
A．B．
C．D．
6．如图，、、是的切线，切点分别为P、C、D．若，，则的长是（ ）

A．3B．3.5C．4D．4.5
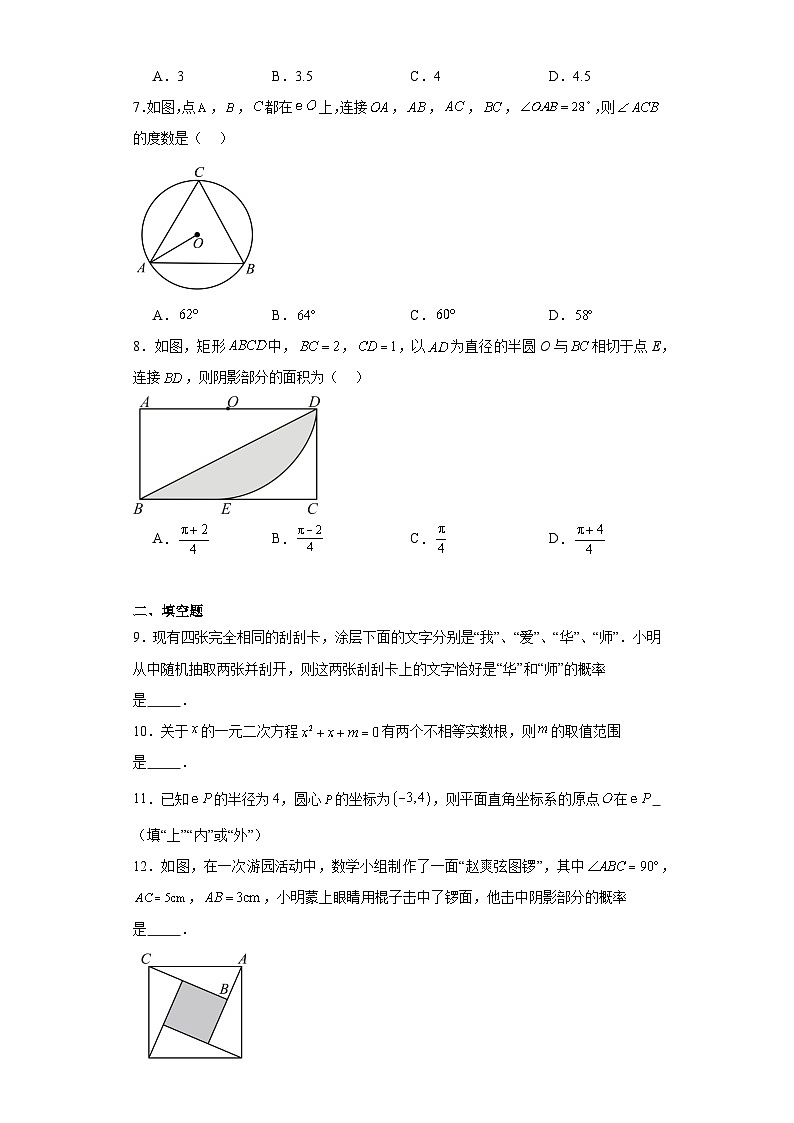
7．如图，点，，都在上，连接，，，，，则的度数是（ ）
A．B．C．D．
8．如图，矩形中，，，以为直径的半圆O与相切于点E，连接，则阴影部分的面积为（ ）

A．B．C．D．
二、填空题
9．现有四张完全相同的刮刮卡，涂层下面的文字分别是“我”、“爱”、“华”、“师”．小明从中随机抽取两张并刮开，则这两张刮刮卡上的文字恰好是“华”和“师”的概率是 ．
10．关于的一元二次方程有两个不相等实数根，则的取值范围是 ．
11．已知的半径为4，圆心的坐标为，则平面直角坐标系的原点在 （填“上”“内”或“外”）
12．如图，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中，，，小明蒙上眼睛用棍子击中了锣面，他击中阴影部分的概率是 ．

13．如图①，在等腰直角三角形中，分别以点A、C为圆心，长为半径作弧，两弧在内围成如图①所示的阴影部分，用5个阴影部分的图案拼成如图②的图形，若，则图②图形的周长为 ．
14．如图，是的直径，弦，垂足为点E，，则 ．
15．对于一元二次方程，下列说法：
①若方程有一根，则；
②若，则；
③若方程的两个根是，那么方程的两个根为；
④若c是方程的一个根，则一定有成立．
其中正确的是 ．（填序号）
16．如图，在中，，，则的度数是 ．

三、解答题
17．有一张长为，宽的长方形薄钢片，在它的四个角上各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为．那么钢片各角切去的正方形的边长是多少？
18．乒乓球被称为中国的“国球”，是一种世界流行的球类体育项目．某乒乓球训练班中甲、乙两名选手在5次训练中的成绩（单位：分）依次为甲：8，8，7，8，9；乙：5，9，7，10，9．教练根据他们的成绩绘制了如下的统计表：
根据以上信息，解答下面的问题：
(1)填空：a＝ ，b＝ ，c＝ ；
(2)计算甲同学成绩的方差；
(3)已知乙同学的成绩的方差是，请问谁的成绩更稳定？
19．已知关于x的一元二次方程.
(1)求证：对于任意实数k，方程总有两个不相等的实根；
(2)若方程的一个根是2，求k的值及方程的另一个根.
20．浙教版八年级下册数学教材第页探究活动：已知数据，，，，，把这组数据的每个数都减去，得到一组新数据将这两组数据画成折线图，并用一条平行于横轴的直线来表示这两组数据的平均数观察你画的两个图形，你发现了哪些有趣的结论？
(1)请在两个网格图中画出相应图形；
(2)观察你画的两个图形，可以发现：
①一组数据中每个数据加上一个相同的实数，得到一组新数据的平均数______；
②一组数据中每个数据加上一个相同的实数，得到一组新数据的方差______．
(3)根据你的结论解决问题：
若一组数据，，，，的平均数为，方差为，那么数据，，，，的平均数是______，方差是______．
21．学校准备在教学楼后面搭建一个简易的矩形自行车车棚，一边利用数学楼的后墙（可利用的墙长为），另外三边利用学校现有总长的铁栏围成，试设计一种搭法，使得矩形车棚的面积为．

22．如图所示，已知为的直径，是弦，且于点E．连接、．
(1)求证：；
(2)若，求的直径．
23．如图，以四边形的对角线为直径作圆，圆心为，过点作的延长线于点，已知平分．

(1)求证：是切线；
(2)如图1，若，，求的半径和的长；
(3)如图2，在（2）的条件下，连接，若，求图中阴影部分的面积．
成绩/分
平均数
众数
中位数
甲
8
b
8
乙
a
9
c
参考答案：
1．D
【分析】本题考查方差的意义和平均数的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
【详解】解：收入平均数变大，方差变小最能体现发展生产力，消除两极分化，
故选D．
2．B
【分析】本题考查根的判别式，解一元二次方程，先利用根的判别式的意义得到，求出的值可得到方程为，然后利用因式分解法解方程．解题的关键是掌握：式子是一元二次方程根的判别式，方程有两个不等的实数根；方程有两个相等的实数根；方程无实数根．
【详解】解：∵关于的一元二次方程有两个相等的实数根，
∴，
解得：，
此时方程化为，
，
，
∴．
故选：B．
3．B
【分析】本题考查算术平均数的计算，一般的每个数据扩大n倍后，数据的平均数也扩大n倍．每个数据增加同一个常数，数据的平均数也增加同一个常数，据此解析即可．
【详解】解：∵，，…，的平均数为2，
∴，
∴，
故选B．
4．A
【分析】本题考查扇形面积的计算，关键是掌握扇形面积的计算公式．由扇形面积的计算公式，即可计算．
【详解】解：扇形的面积
故选：A．
5．C
【分析】本题考查的是由实际问题抽象出一元二次方程的平均增长率问题．解决这类问题的关键是找出等量关系列出一元二次方程．2021年手机支付用户约为亿人，2022年手机支付用户约为亿人，根据等量关系列出方程求解即可．
【详解】解：设第一年的增长率为，依题意，得
．
故选：C．
6．A
【分析】本题考查了切线长定理，熟练掌握切线长定理是解题关键．根据切线长定理可得，由此即可得．
【详解】解：、、是的切线，切点分别为、、，
，
，，
，
故选：A．
7．A
【分析】本题主要考查了圆周角定理，解题的关键是掌握圆周角定理．连接，由，可得，进而得到，最后根据圆周角定理即可求解．
【详解】连接，
，
，
，
，
故选：A．
8．C
【分析】连接交于点，根据切线的性质可得，可得到四边形和四边形为矩形，再证得，可得，从而得到阴影部分的面积，即可求解．
【详解】解：连接交于点，如图，

以为直径的半圆与相切于点，
，
，
四边形为矩形，
，
四边形和四边形为矩形，
，，
在和中，
，
，
，
阴影部分的面积．
故选：C．
【点睛】此题考查切线的性质及扇形面积的计算，全等三角形的性质，矩形的性质，切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
9．
【分析】本题主要考查列表或画树状图求随机事件的概率，掌握列表或画树状图的方法，求概率的计算方法是解题的关键．
根据题意画树状图即可求解．
【详解】解：画树状图表示所有等可能结果如下，
共有种等可能结果，其中文字恰好是“华”和“师”的结果有种，
∴文字恰好是“华”和“师”的概率是，
故答案为：．
10．
【分析】本题考查了一元二次方程的根的判别式．熟练掌握有两个不相等的实数根，则是解题的关键．
根据，计算求解即可．
【详解】解：由题意知，，
解得，，
故答案为：．
11．外
【分析】本题主要考查点与圆的位置关系，点与圆的位置关系有3种．设的半径为，点到圆心的距离，则有：点在圆外；点在圆上；点在圆内．
先根据点坐标求出点到原点的距离，再判断与圆的半径的大小关系，从而得出答案．
【详解】解：∵圆心的坐标为，
又的半径，
∴原点在外，
故答案为：外．
12．
【分析】本题考查了勾股定理，几何概率．正确求解阴影部分的面积是解题的关键．
由勾股定理得，，根据，计算求解，根据概率为，计算求解即可．
【详解】解：由勾股定理得，，
∴，
∴他击中阴影部分的概率是，
故答案为：．
13．
【分析】本题主要考查等腰直角三角形的性质，弧长公式，熟练掌握弧长公式是解题的关键．根据弧长公式求出每段弧长即可得到答案．
【详解】解：为等腰直角三角形，
，
，
故每段弧长为，
故图②图形的周长为．
故答案为：．
14．10
【分析】本题主要考查垂径定理、勾股定理，熟练掌握垂径定理以及勾股定理是解决本题的关键．根据得，进而根据垂径定理得出，连接，设，则，根据勾股定理得方程解答．
【详解】解：连接，设，则，
∵，
∴，
∵是的直径，弦，
∴，
在中，根据勾股定理得，
，
解得，
即的长为10．
故答案为：10．
15．①②③
【分析】本题考查一元二次方程的解，根的判别式，分别根据一元二次方程的解，根的判别式判断即可．
【详解】解：①若方程有一根，则，故正确；
②若，则可知方程有一个根为，
则，故正确；
③若方程的两个根是，
则或4，
所以方程的两个根为，故正确；
④若c是方程的一个根，
则，
当时，则一定有成立，故错误．
所以其中正确的是①②③．
故答案为：①②③．
16．/40度
【分析】本题考查的是圆周角定理，利用在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得的度数．
【详解】解：，，
，
故答案为：．
17．钢片各角切去的正方形的边长是．
【分析】设钢片各角切去的正方形的边长是．根据无盖方盒的底面积为列出一元二次方程，解方程即可得到答案，此题考查了一元二次方程的应用，读懂题意，正确列出方程是解题的关键．
【详解】解：设钢片各角切去的正方形的边长是．
由题意得：
化简得：
解得：，（舍）
答：钢片各角切去的正方形的边长是．
18．(1)8，8，9
(2)
(3)甲的成绩比较稳定
【分析】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义是解题的关键．方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
（1）根据平均数、众数和中位数的定义求解；
（2）根据方差公式求解；
（3）根据方差的意义求解．
【详解】（1）解：由题意可得
甲的众数，
乙的平均数，
乙的中位数；
故答案为：8，8，9；
（2）解：甲同学的方差为：
（3）甲的成绩的方差小于乙的成绩的方差，说明甲的成绩比较稳定
19．(1)见解析
(2)k的值为1，方程的另一个根为
【分析】本题考查了根与系数的关系：若，是一元二次方程的两根时，，．也考查了根的判别式．
（1）通过计算判别式的值得到，从而可判断方程根的情况；
（2）设方程的另一个根为，根据根与系数的关系得到设方程的两个根分别为，，则，然后再求出的值．
【详解】（1）证明：∵，
∴对于任意实数k，方程总有两个不相等的实数根.
（2）设方程的两个根分别为，，则
，
∴.
∴.
∴.
故k的值为1，方程的另一个根为.
20．(1)见解析
(2)①增加n；②不变
(3)，
【分析】本题考查折线统计图、平均数与方差；
（1）根据题意画出图形即可；
（2）①根据图形，结合平均数的定义即可求解；②根据图形，结合方差的意义即可求解；
（3）根据（2）的结论即可求解；
理解方差和平均数的意义，利用数形结合的思想解答是解题的关键．
【详解】（1）解：如图所示：
（2）解：观察图形，可以发现：
①一组数据中每个数据加上一个相同的实数，得到一组新数据的平均数增加．
故答案为：增加；
②一组数据中每个数据加上一个相同的实数，得到一组新数据的方差不变．
故答案为：不变；
（3）解：根据的结论（2）可知：
若一组数据，，，，的平均数为，方差为，
那么数据，，，，的平均数是，方差是．
故答案为：，．
21．长为20米，宽为15米．
【分析】此题主要考查了一元二次方程的应用，首先要注意读懂题意，正确理解题意，然后才能利用题目的数量关系列出方程．
设，用长方形的周长表示出，即可根据矩形面积公式列出方程，求解即可．
【详解】解：设，则；
根据题意列方程为，，
解得，；
当，（米，而墙长25米，不合题意舍去
当，（米．
答：若围成的面积为，自行车车棚的长和宽分别为20米，15米．
22．(1)证明见解析
(2)
【分析】（1）先根据垂径定理求出，再根据圆周角定理即可得出，再由等腰三角形的性质即可得出结论；
（2）设，则，在中根据勾股定理求出k的值，进而可得出结论．
此题考查了垂径定理、圆周角定理、勾股定理等知识，熟练掌握垂径定理是解题的关键．
【详解】（1）证明：∵为的直径，是弦，且于点E，
∴，
∴，
∵，
∴，
∴；
（2）解：设，则，
∵为的直径，是弦，且于点E，
∴，
在中，，
即，
解得或（不合题意，舍去），
∴．
即的直径为．
23．(1)见解析
(2)5，
(3)
【分析】（1）连接，根据已知条件证明即可解决问题；（2）取中点，连接，根据垂径定理可得，所以四边形是矩形，利用勾股定理即可求出结果；（3）由（2）可知四边形是矩形，可得，，即可求解．
【详解】（1）证明：如图，连接，

，
．
平分，
，
又，
，
，
，
是切线；
（2）如图，作于点．
由（1）知，
四边形是矩形，
，，
．
在中，，
，
在中，，
，

的长是．
（3）连接，，

四边形是矩形

．
【点睛】本题考查了切线的判定与性质，垂径定理，圆周角定理，勾股定理，解决本题的关键是掌握切线的判定与性质．